
Question Number 214040 by ajfour last updated on 25/Nov/24
Commented by ajfour last updated on 25/Nov/24

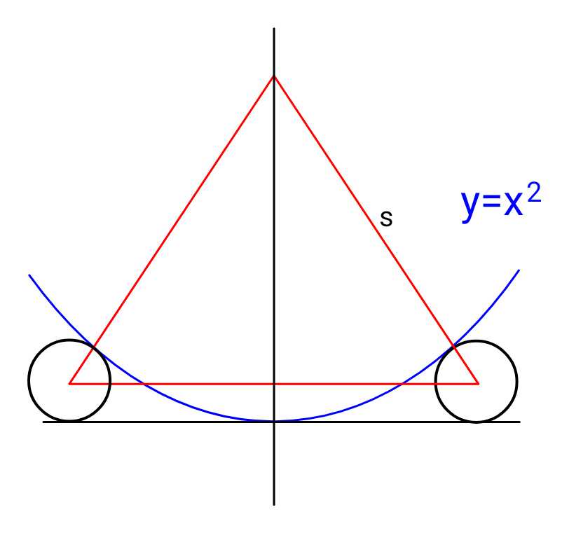
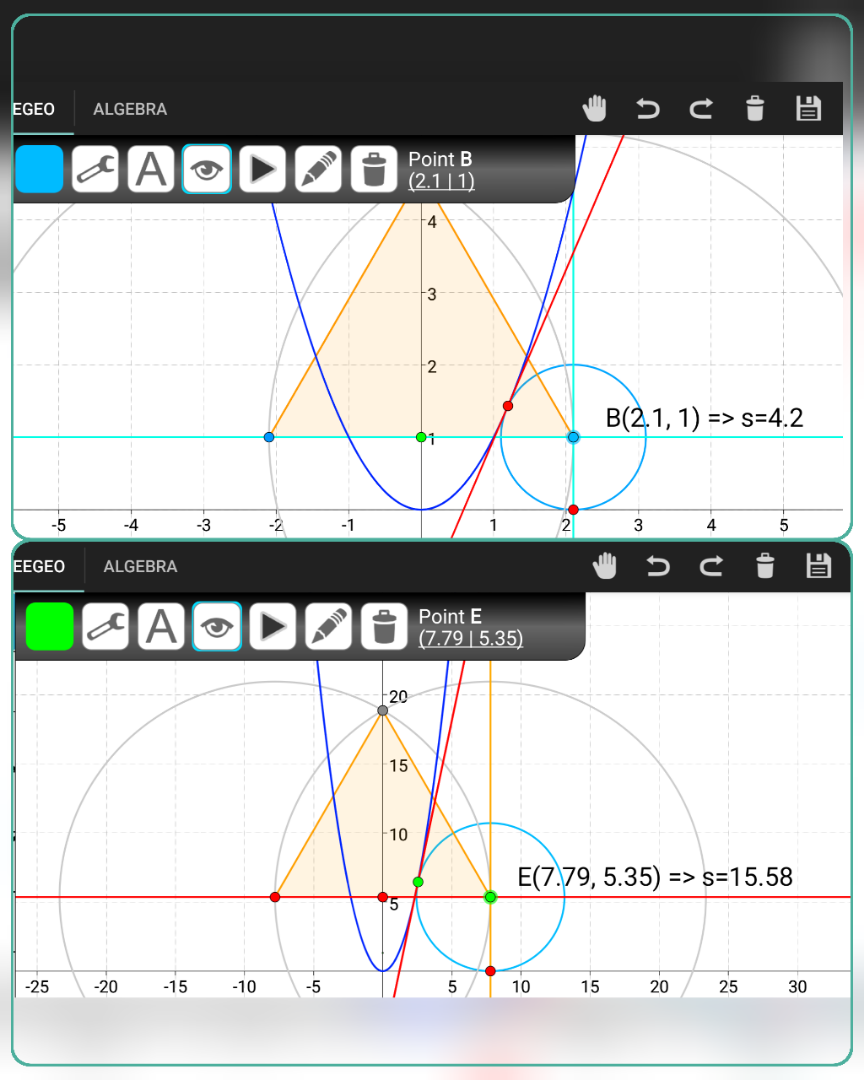
$${The}\:\bigtriangleup\:{is}\:{equilateral}.\:{Find}\:{its}\:{side}\:\boldsymbol{{s}}. \\ $$
Answered by mr W last updated on 25/Nov/24
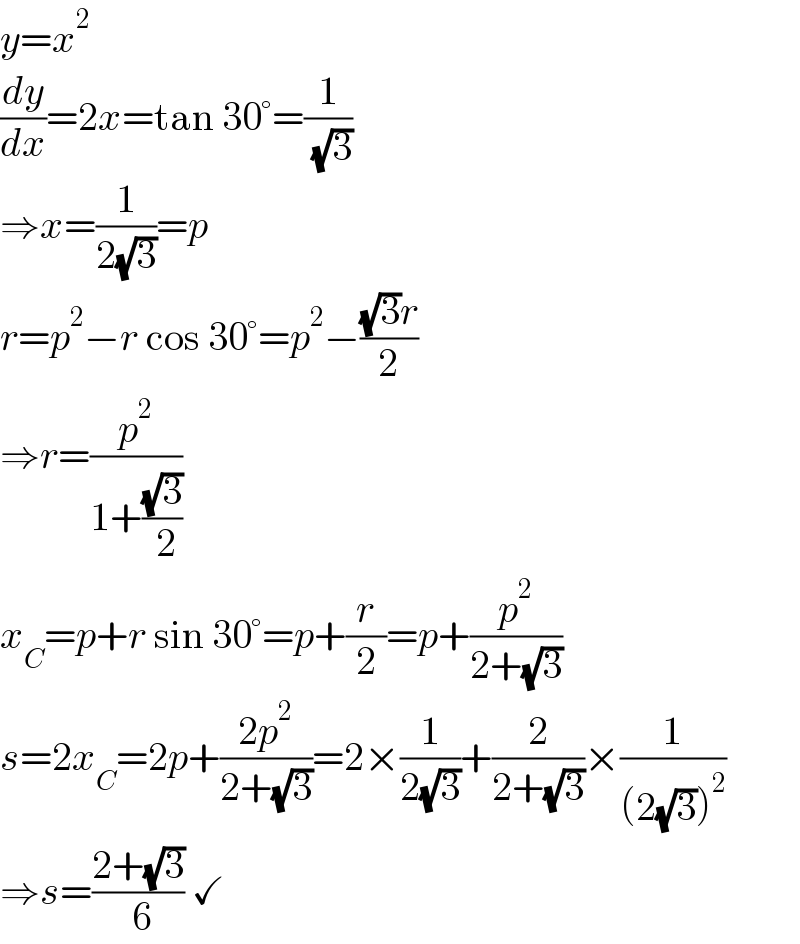
$${y}={x}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{x}=\mathrm{tan}\:\mathrm{30}°=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}={p} \\ $$$${r}={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\mathrm{30}°={p}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}{r}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{{p}^{\mathrm{2}} }{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\:\mathrm{2}}} \\ $$$${x}_{{C}} ={p}+{r}\:\mathrm{sin}\:\mathrm{30}°={p}+\frac{{r}}{\mathrm{2}}={p}+\frac{{p}^{\mathrm{2}} }{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${s}=\mathrm{2}{x}_{{C}} =\mathrm{2}{p}+\frac{\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{2}+\sqrt{\mathrm{3}}}=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\mathrm{2}+\sqrt{\mathrm{3}}}×\frac{\mathrm{1}}{\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{s}=\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\:\mathrm{6}}\:\checkmark \\ $$
Commented by mr W last updated on 25/Nov/24
Commented by ajfour last updated on 25/Nov/24

$${Thank}\:{you}\:{Sir}. \\ $$
Commented by nikif99 last updated on 25/Nov/24
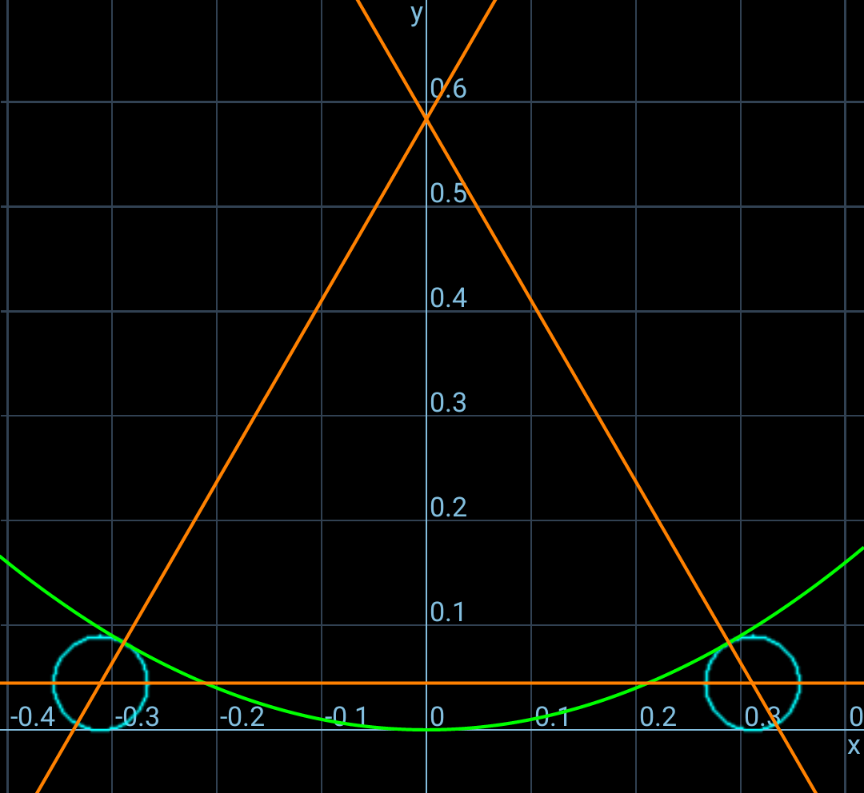
$${Is}\:{there}\:{a}\:{unique}\:{solution},\:{even}\:{in} \\ $$$${relation}\:{to}\:{r}? \\ $$
Commented by nikif99 last updated on 25/Nov/24
Commented by mr W last updated on 25/Nov/24

$${two}\:{sides}\:{of}\:{the}\:{equilateral}\:{should} \\ $$$${be}\:{the}\:{normals}\:{of}\:{the}\:{parabola}, \\ $$$${therefore}\:{there}\:{is}\:{an}\:{unique}\: \\ $$$${solution}. \\ $$
Commented by nikif99 last updated on 25/Nov/24

$${Thank}\:{you},\:{Sir}. \\ $$
