Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 214020 by ajfour last updated on 24/Nov/24

Commented by ajfour last updated on 24/Nov/24

Red area = Blue area. Find r in terms of k, φ.

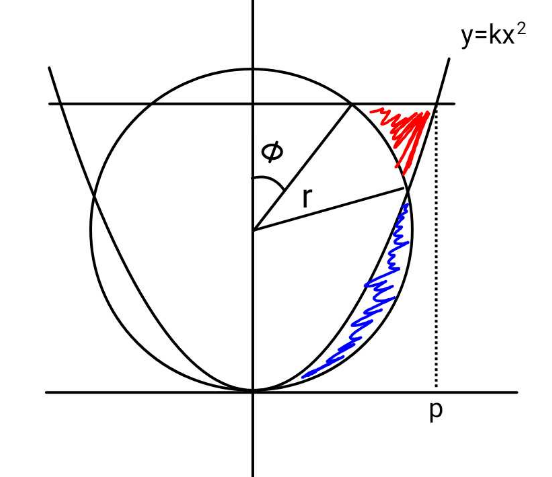
$${Red}\:{area}\:=\:{Blue}\:{area}.\:{Find}\:{r}\:{in} \\ $$$${terms}\:{of}\:{k},\:\phi. \\ $$

Answered by dionigi last updated on 24/Nov/24

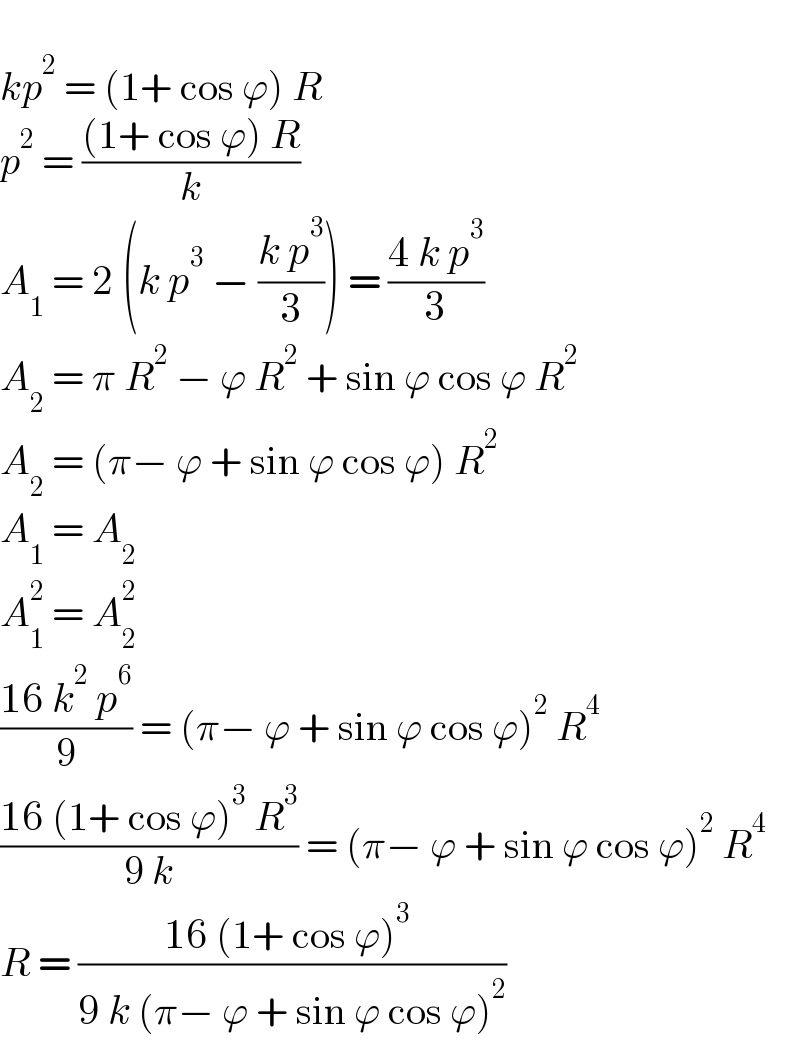
kp^2 = (1+ cos ϕ) R p^2 = (((1+ cos ϕ) R)/k) A_1 = 2 (k p^3 − ((k p^3 )/3)) = ((4 k p^3 )/3) A_2 = π R^2 − ϕ R^2 + sin ϕ cos ϕ R^2 A_2 = (π− ϕ + sin ϕ cos ϕ) R^2 A_1 = A_2 A_1 ^2 = A_2 ^2 ((16 k^2 p^6 )/9) = (π− ϕ + sin ϕ cos ϕ)^2 R^4 ((16 (1+ cos ϕ)^3 R^3 )/(9 k)) = (π− ϕ + sin ϕ cos ϕ)^2 R^4 R = ((16 (1+ cos ϕ)^3 )/(9 k (π− ϕ + sin ϕ cos ϕ)^2 ))

$$ \\ $$$${kp}^{\mathrm{2}} \:=\:\left(\mathrm{1}+\:\mathrm{cos}\:\varphi\right)\:{R} \\ $$$${p}^{\mathrm{2}} \:=\:\frac{\left(\mathrm{1}+\:\mathrm{cos}\:\varphi\right)\:{R}}{{k}} \\ $$$${A}_{\mathrm{1}} \:=\:\mathrm{2}\:\left({k}\:{p}^{\mathrm{3}} \:−\:\frac{{k}\:{p}^{\mathrm{3}} }{\mathrm{3}}\right)\:=\:\frac{\mathrm{4}\:{k}\:{p}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${A}_{\mathrm{2}} \:=\:\pi\:{R}^{\mathrm{2}} \:−\:\varphi\:{R}^{\mathrm{2}} \:+\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:{R}^{\mathrm{2}} \\ $$$${A}_{\mathrm{2}} \:=\:\left(\pi−\:\varphi\:+\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\right)\:{R}^{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} \:=\:{A}_{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} ^{\mathrm{2}} \:=\:{A}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\frac{\mathrm{16}\:{k}^{\mathrm{2}} \:{p}^{\mathrm{6}} }{\mathrm{9}}\:=\:\left(\pi−\:\varphi\:+\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} \:{R}^{\mathrm{4}} \\ $$$$\frac{\mathrm{16}\:\left(\mathrm{1}+\:\mathrm{cos}\:\varphi\right)^{\mathrm{3}} \:{R}^{\mathrm{3}} }{\mathrm{9}\:{k}}\:=\:\left(\pi−\:\varphi\:+\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} \:{R}^{\mathrm{4}} \\ $$$${R}\:=\:\frac{\mathrm{16}\:\left(\mathrm{1}+\:\mathrm{cos}\:\varphi\right)^{\mathrm{3}} \:}{\mathrm{9}\:{k}\:\left(\pi−\:\varphi\:+\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} } \\ $$

Commented by ajfour last updated on 24/Nov/24

Thank you.

$${Thank}\:{you}. \\ $$

Answered by mr W last updated on 24/Nov/24

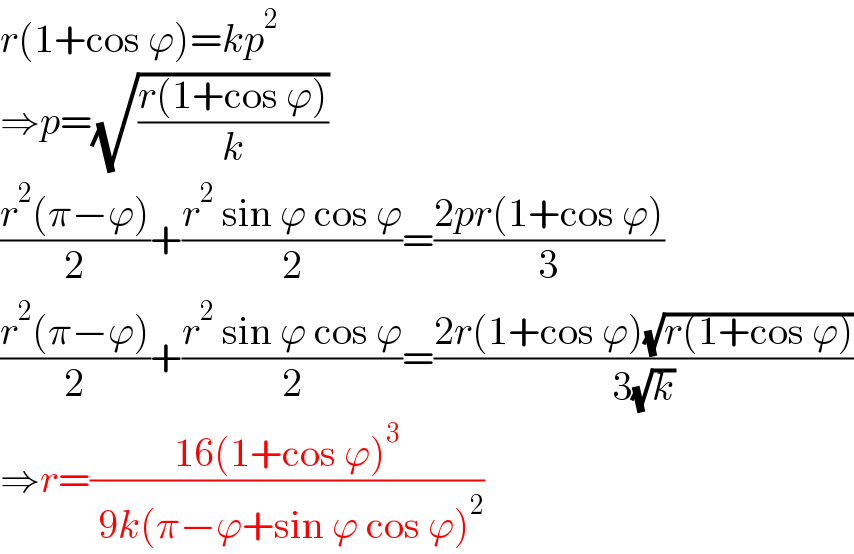
r(1+cos ϕ)=kp^2 ⇒p=(√((r(1+cos ϕ))/k)) ((r^2 (π−ϕ))/2)+((r^2 sin ϕ cos ϕ)/2)=((2pr(1+cos ϕ))/3) ((r^2 (π−ϕ))/2)+((r^2 sin ϕ cos ϕ)/2)=((2r(1+cos ϕ)(√(r(1+cos ϕ))))/(3(√k))) ⇒r=((16(1+cos ϕ)^3 )/( 9k(π−ϕ+sin ϕ cos ϕ)^2 ))

$${r}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)={kp}^{\mathrm{2}} \\ $$$$\Rightarrow{p}=\sqrt{\frac{{r}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}{{k}}} \\ $$$$\frac{{r}^{\mathrm{2}} \left(\pi−\varphi\right)}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} \:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi}{\mathrm{2}}=\frac{\mathrm{2}{pr}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}{\mathrm{3}} \\ $$$$\frac{{r}^{\mathrm{2}} \left(\pi−\varphi\right)}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} \:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi}{\mathrm{2}}=\frac{\mathrm{2}{r}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)\sqrt{{r}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}}{\mathrm{3}\sqrt{{k}}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{16}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)^{\mathrm{3}} }{\:\mathrm{9}{k}\left(\pi−\varphi+\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} } \\ $$

Commented by mr W last updated on 24/Nov/24

Commented by mr W last updated on 24/Nov/24

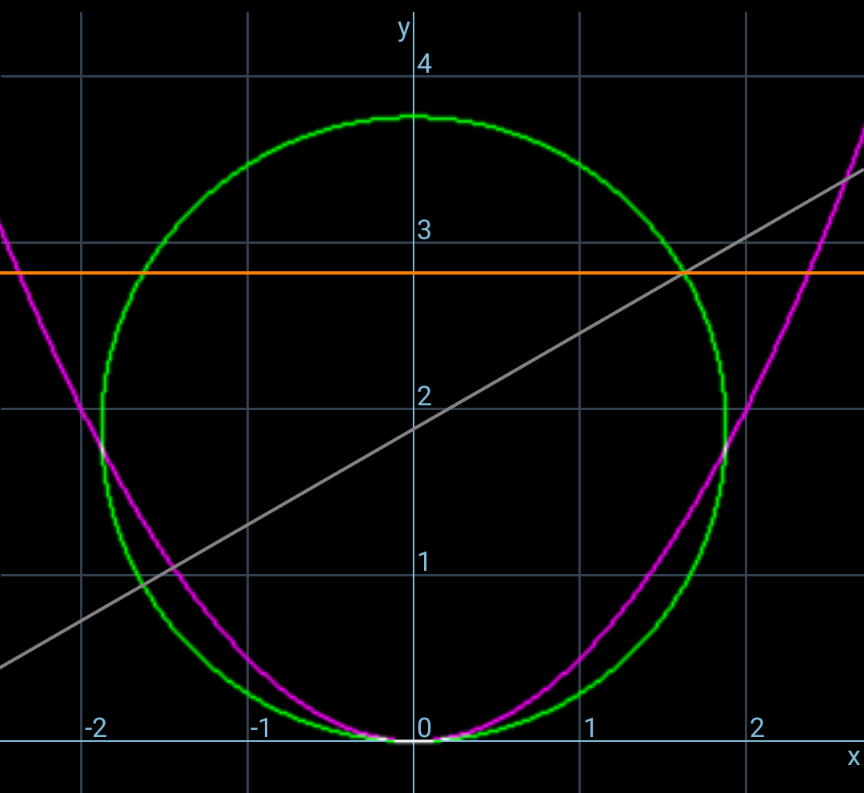
Commented by ajfour last updated on 24/Nov/24

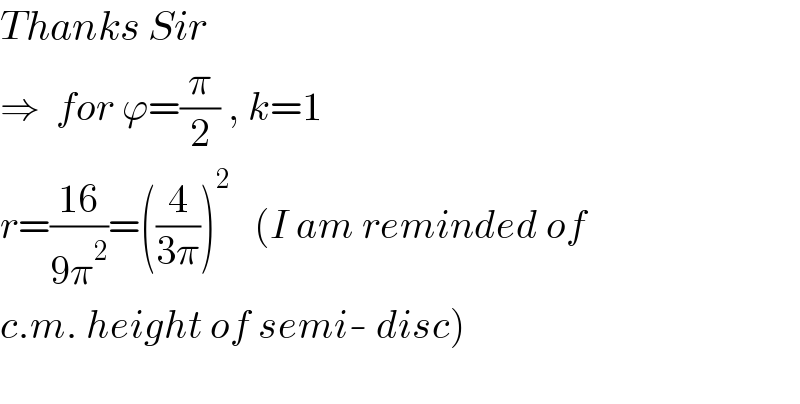
Thanks Sir ⇒ for ϕ=(π/2) , k=1 r=((16)/(9π^2 ))=((4/(3π)))^2 (I am reminded of c.m. height of semi- disc)

$${Thanks}\:{Sir} \\ $$$$\Rightarrow\:\:{for}\:\varphi=\frac{\pi}{\mathrm{2}}\:,\:{k}=\mathrm{1} \\ $$$${r}=\frac{\mathrm{16}}{\mathrm{9}\pi^{\mathrm{2}} }=\left(\frac{\mathrm{4}}{\mathrm{3}\pi}\right)^{\mathrm{2}} \:\:\:\left({I}\:{am}\:{reminded}\:{of}\:\right. \\ $$$$\left.{c}.{m}.\:{height}\:{of}\:{semi}-\:{disc}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com