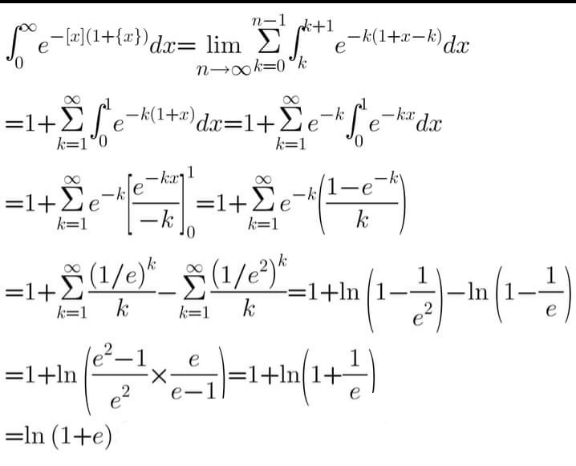Question Number 213945 by Spillover last updated on 22/Nov/24
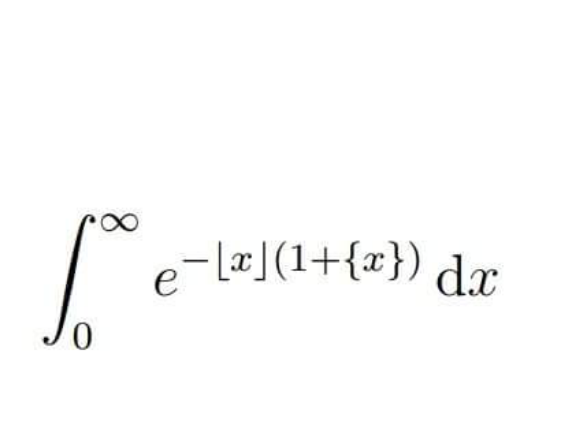
Answered by mathmax last updated on 23/Nov/24
) dx =1+Σ_(n=1) ^∞ ∫_n ^(n+1) e^(−n(1+x−n)) dx =1+Σ_(n=1) ^∞ ∫_n ^(n+1) e^(−n+n^2 ) e^(−nx) dx =1+Σ_(n=1) ^∞ e^(−n+n^2 ) [−(1/n)e^(−nx) ]_n ^(n+1) =1−Σ_(n=1) ^∞ (e^(n^2 −n) /n){ e^(−n^2 −n) −e^(−n^2 ) } =1−Σ_(n=1) ^∞ (e^(−2n) /n)+Σ_(n=1) ^∞ (e^(−n) /n) on rappelle que Σ (z^n /n)=−ln(1−z) pour ∣z∣<1 I=1+ln(1−e^(−2) )−ln(1−e^(−1) ) =1+ln(1−(1/e^2 ))−ln(1−(1/e))](Q213965.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left[{x}\right]\left(\mathrm{1}+{x}−\left[{x}\right]\right)} {dx} \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \int_{{n}} ^{{n}+\mathrm{1}} \:{e}^{−{n}\left(\mathrm{1}+{x}−{n}\right)} {dx} \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \int_{{n}} ^{{n}+\mathrm{1}} {e}^{−{n}+{n}^{\mathrm{2}} } \:{e}^{−{nx}} {dx} \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} {e}^{−{n}+{n}^{\mathrm{2}} } \left[−\frac{\mathrm{1}}{{n}}{e}^{−{nx}} \right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$=\mathrm{1}−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{e}^{{n}^{\mathrm{2}} −{n}} }{{n}}\left\{\:{e}^{−{n}^{\mathrm{2}} −{n}} −{e}^{−{n}^{\mathrm{2}} } \right\} \\ $$$$=\mathrm{1}−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{e}^{−\mathrm{2}{n}} }{{n}}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}} \\ $$$${on}\:{rappelle}\:{que}\:\Sigma\:\frac{{z}^{{n}} }{{n}}=−{ln}\left(\mathrm{1}−{z}\right)\:{pour}\:\mid{z}\mid<\mathrm{1} \\ $$$${I}=\mathrm{1}+{ln}\left(\mathrm{1}−{e}^{−\mathrm{2}} \right)−{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right) \\ $$$$=\mathrm{1}+{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\right)−{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{e}}\right) \\ $$
Commented by mr W last updated on 23/Nov/24

$$=\mathrm{1}+\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}\right) \\ $$
Commented by mehdee7396 last updated on 23/Nov/24

$$={ln}\left({e}+\mathrm{1}\right) \\ $$
Commented by Spillover last updated on 26/Nov/24

$${right} \\ $$
Answered by Spillover last updated on 23/Nov/24

Answered by Spillover last updated on 23/Nov/24