Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 213923 by luj last updated on 21/Nov/24

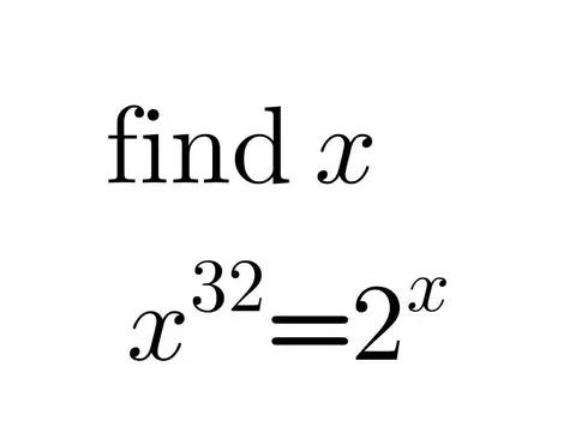
Answered by MATHEMATICSAM last updated on 21/Nov/24

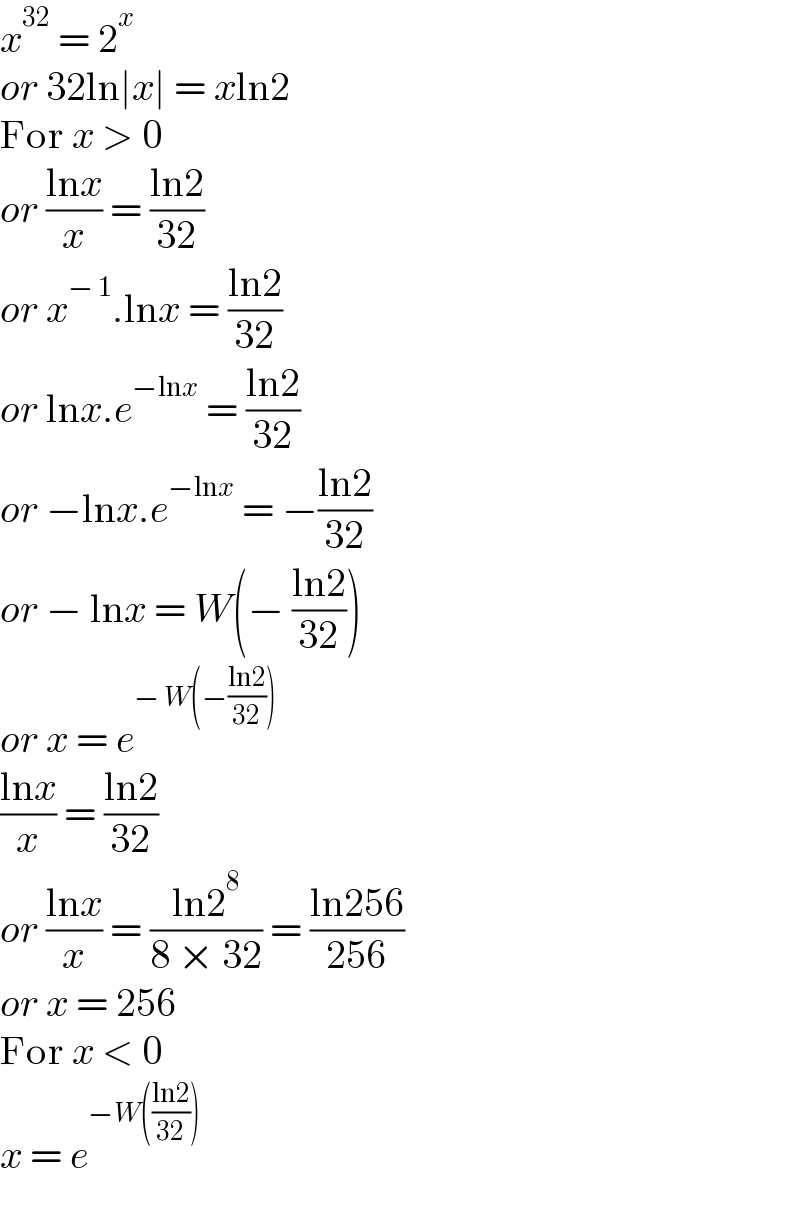
x^(32) = 2^x or 32ln∣x∣ = xln2 For x > 0 or ((lnx)/x) = ((ln2)/(32)) or x^(− 1) .lnx = ((ln2)/(32)) or lnx.e^(−lnx) = ((ln2)/(32)) or −lnx.e^(−lnx) = −((ln2)/(32)) or − lnx = W(− ((ln2)/(32))) or x = e^(− W(−((ln2)/(32)))) ((lnx)/x) = ((ln2)/(32)) or ((lnx)/x) = ((ln2^8 )/(8 × 32)) = ((ln256)/(256)) or x = 256 For x < 0 x = e^(−W(((ln2)/(32))))

$${x}^{\mathrm{32}} \:=\:\mathrm{2}^{{x}} \\ $$$${or}\:\mathrm{32ln}\mid{x}\mid\:=\:{x}\mathrm{ln2} \\ $$$$\mathrm{For}\:{x}\:>\:\mathrm{0} \\ $$$${or}\:\frac{\mathrm{ln}{x}}{{x}}\:=\:\frac{\mathrm{ln2}}{\mathrm{32}}\: \\ $$$${or}\:{x}^{−\:\mathrm{1}} .\mathrm{ln}{x}\:=\:\frac{\mathrm{ln2}}{\mathrm{32}} \\ $$$${or}\:\mathrm{ln}{x}.{e}^{−\mathrm{ln}{x}} \:=\:\frac{\mathrm{ln2}}{\mathrm{32}} \\ $$$${or}\:−\mathrm{ln}{x}.{e}^{−\mathrm{ln}{x}} \:=\:−\frac{\mathrm{ln2}}{\mathrm{32}} \\ $$$${or}\:−\:\mathrm{ln}{x}\:=\:{W}\left(−\:\frac{\mathrm{ln2}}{\mathrm{32}}\right) \\ $$$${or}\:{x}\:=\:{e}^{−\:{W}\left(−\frac{\mathrm{ln2}}{\mathrm{32}}\right)} \\ $$$$\frac{\mathrm{ln}{x}}{{x}}\:=\:\frac{\mathrm{ln2}}{\mathrm{32}} \\ $$$${or}\:\frac{\mathrm{ln}{x}}{{x}}\:=\:\frac{\mathrm{ln2}^{\mathrm{8}} }{\mathrm{8}\:×\:\mathrm{32}}\:=\:\frac{\mathrm{ln256}}{\mathrm{256}} \\ $$$${or}\:{x}\:=\:\mathrm{256} \\ $$$$\mathrm{For}\:{x}\:<\:\mathrm{0}\:\: \\ $$$${x}\:=\:{e}^{−{W}\left(\frac{\mathrm{ln2}}{\mathrm{32}}\right)} \\ $$

Answered by mr W last updated on 21/Nov/24

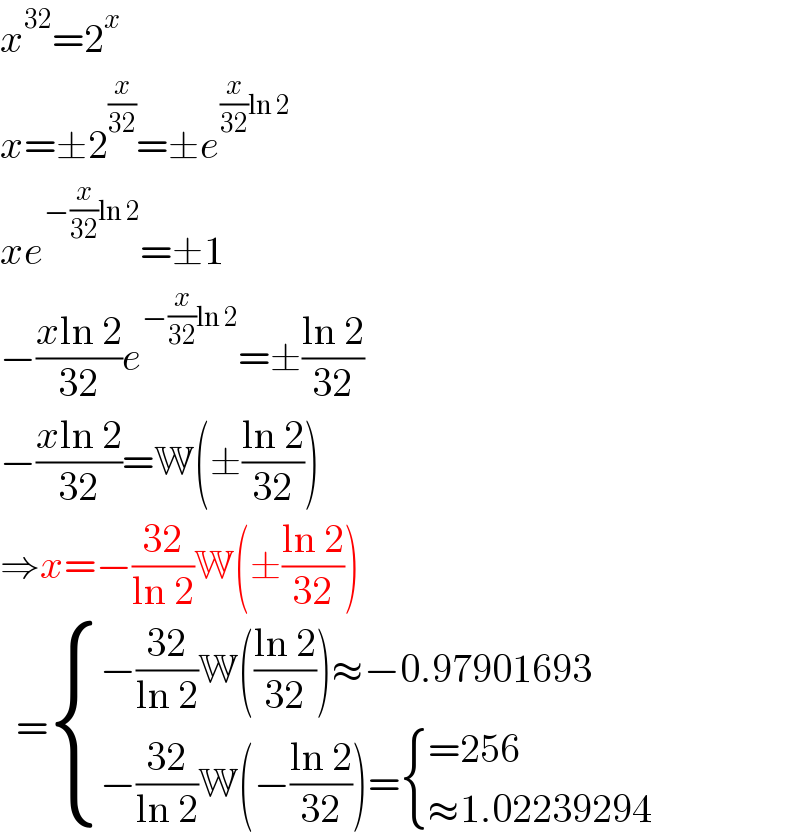
x^(32) =2^x x=±2^(x/(32)) =±e^((x/(32))ln 2) xe^(−(x/(32))ln 2) =±1 −((xln 2)/(32))e^(−(x/(32))ln 2) =±((ln 2)/(32)) −((xln 2)/(32))=W(±((ln 2)/(32))) ⇒x=−((32)/(ln 2))W(±((ln 2)/(32))) = { ((−((32)/(ln 2))W(((ln 2)/(32)))≈−0.97901693)),((−((32)/(ln 2))W(−((ln 2)/(32)))= { ((=256)),((≈1.02239294)) :})) :}

$${x}^{\mathrm{32}} =\mathrm{2}^{{x}} \\ $$$${x}=\pm\mathrm{2}^{\frac{{x}}{\mathrm{32}}} =\pm{e}^{\frac{{x}}{\mathrm{32}}\mathrm{ln}\:\mathrm{2}} \\ $$$${xe}^{−\frac{{x}}{\mathrm{32}}\mathrm{ln}\:\mathrm{2}} =\pm\mathrm{1} \\ $$$$−\frac{{x}\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}{e}^{−\frac{{x}}{\mathrm{32}}\mathrm{ln}\:\mathrm{2}} =\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{32}} \\ $$$$−\frac{{x}\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}=\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{32}}{\mathrm{ln}\:\mathrm{2}}\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}\right) \\ $$$$\:\:=\begin{cases}{−\frac{\mathrm{32}}{\mathrm{ln}\:\mathrm{2}}\mathbb{W}\left(\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}\right)\approx−\mathrm{0}.\mathrm{97901693}}\\{−\frac{\mathrm{32}}{\mathrm{ln}\:\mathrm{2}}\mathbb{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{32}}\right)=\begin{cases}{=\mathrm{256}}\\{\approx\mathrm{1}.\mathrm{02239294}}\end{cases}}\end{cases} \\ $$

Answered by kapoorshah last updated on 21/Nov/24

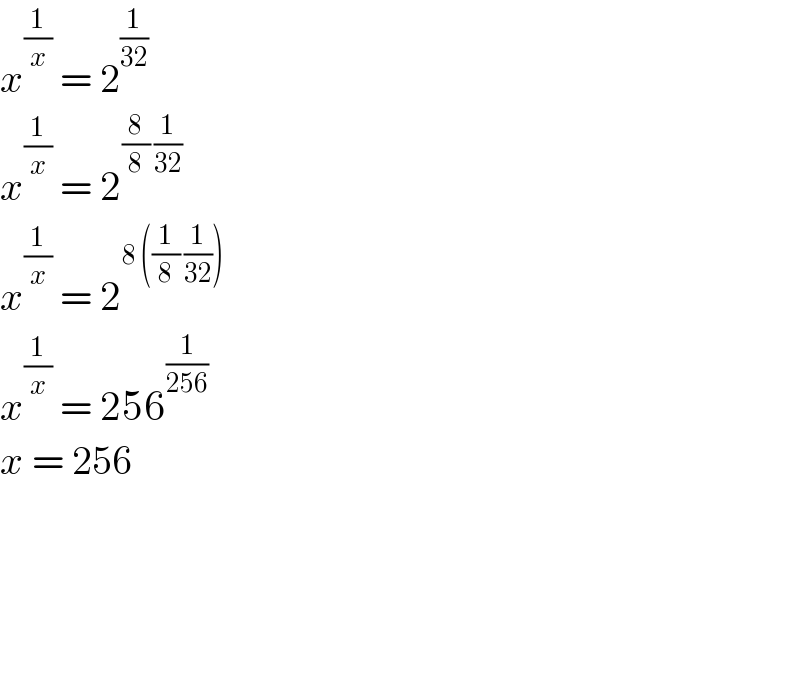
x^(1/x) = 2^(1/(32)) x^(1/x) = 2^((8/8) (1/(32))) x^(1/x) = 2^(8 ((1/8) (1/(32)))) x^(1/x) = 256^(1/(256)) x = 256

$${x}^{\frac{\mathrm{1}}{{x}}} \:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{32}}} \\ $$$${x}^{\frac{\mathrm{1}}{{x}}} \:=\:\mathrm{2}^{\frac{\mathrm{8}}{\mathrm{8}}\:\frac{\mathrm{1}}{\mathrm{32}}} \\ $$$${x}^{\frac{\mathrm{1}}{{x}}} \:=\:\mathrm{2}^{\mathrm{8}\:\left(\frac{\mathrm{1}}{\mathrm{8}}\:\frac{\mathrm{1}}{\mathrm{32}}\right)} \:\: \\ $$$${x}^{\frac{\mathrm{1}}{{x}}} \:=\:\mathrm{256}^{\frac{\mathrm{1}}{\mathrm{256}}} \\ $$$${x}\:=\:\mathrm{256} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 21/Nov/24

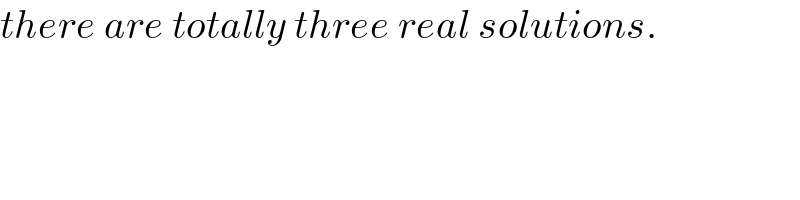
there are totally three real solutions.

$${there}\:{are}\:{totally}\:{three}\:{real}\:{solutions}. \\ $$

Commented by MATHEMATICSAM last updated on 21/Nov/24

yes

$$\mathrm{yes} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com