Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

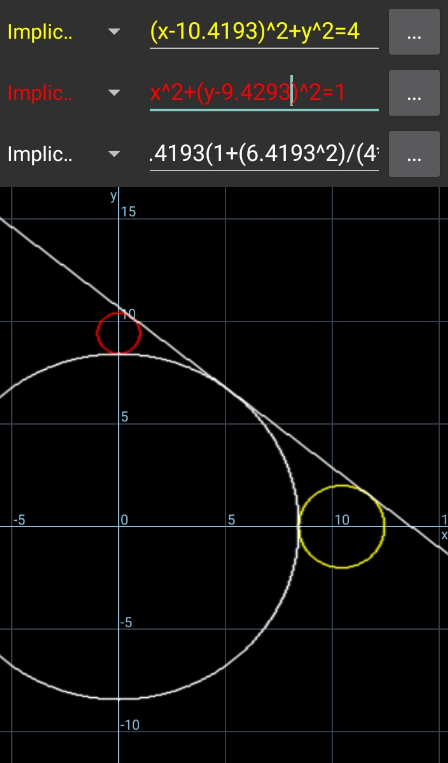
Question Number 213818 by ajfour last updated on 17/Nov/24

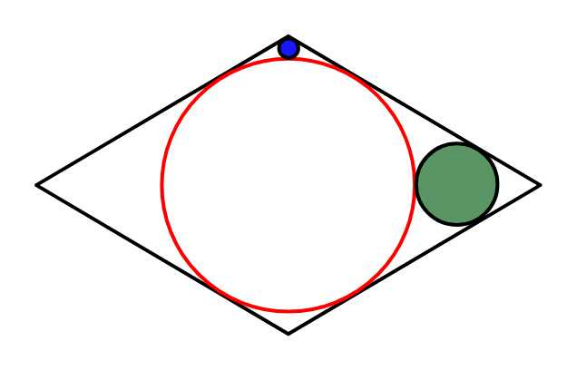
Commented by ajfour last updated on 17/Nov/24

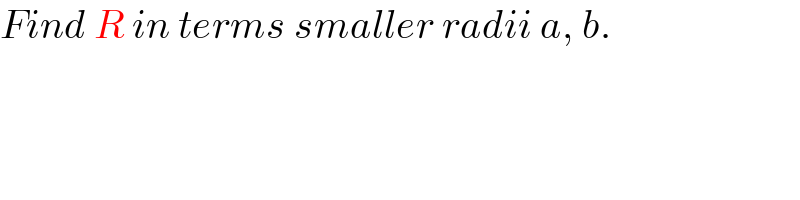
Find R in terms smaller radii a, b.

$${Find}\:{R}\:{in}\:{terms}\:{smaller}\:{radii}\:{a},\:{b}. \\ $$

Answered by mr W last updated on 17/Nov/24

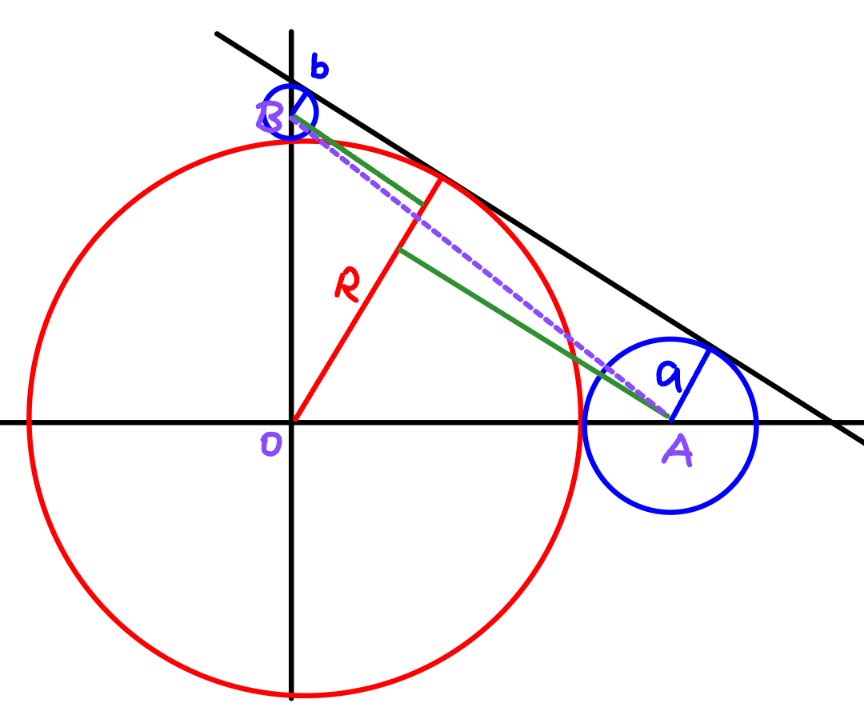
Commented by ajfour last updated on 17/Nov/24

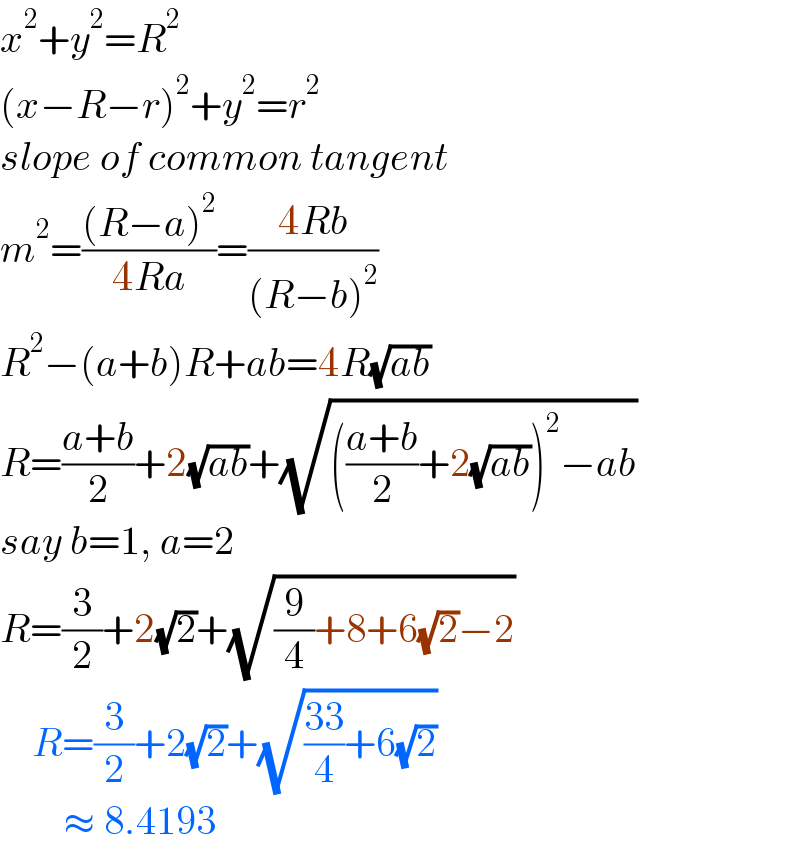
x^2 +y^2 =R^2 (x−R−r)^2 +y^2 =r^2 slope of common tangent m^2 =(((R−a)^2 )/(4Ra))=((4Rb)/((R−b)^2 )) R^2 −(a+b)R+ab=4R(√(ab)) R=((a+b)/2)+2(√(ab))+(√((((a+b)/2)+2(√(ab)))^2 −ab)) say b=1, a=2 R=(3/2)+2(√2)+(√((9/4)+8+6(√2)−2)) R=(3/2)+2(√2)+(√(((33)/4)+6(√2))) ≈ 8.4193

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left({x}−{R}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${slope}\:{of}\:{common}\:{tangent} \\ $$$${m}^{\mathrm{2}} =\frac{\left({R}−{a}\right)^{\mathrm{2}} }{\mathrm{4}{Ra}}=\frac{\mathrm{4}{Rb}}{\left({R}−{b}\right)^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} −\left({a}+{b}\right){R}+{ab}=\mathrm{4}{R}\sqrt{{ab}} \\ $$$${R}=\frac{{a}+{b}}{\mathrm{2}}+\mathrm{2}\sqrt{{ab}}+\sqrt{\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{2}\sqrt{{ab}}\right)^{\mathrm{2}} −{ab}} \\ $$$${say}\:{b}=\mathrm{1},\:{a}=\mathrm{2} \\ $$$${R}=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{8}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{2}} \\ $$$$\:\:\:\:{R}=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\frac{\mathrm{33}}{\mathrm{4}}+\mathrm{6}\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\approx\:\mathrm{8}.\mathrm{4193} \\ $$

Commented by mr W last updated on 17/Nov/24

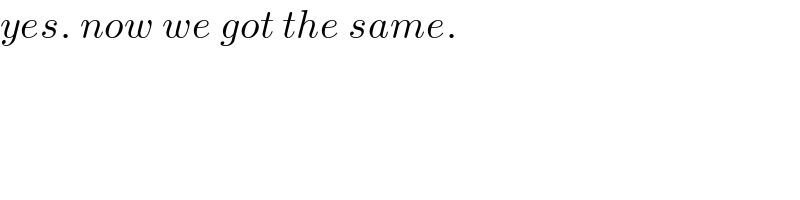
yes. now we got the same.

$${yes}.\:{now}\:{we}\:{got}\:{the}\:{same}. \\ $$

Commented by mr W last updated on 18/Nov/24

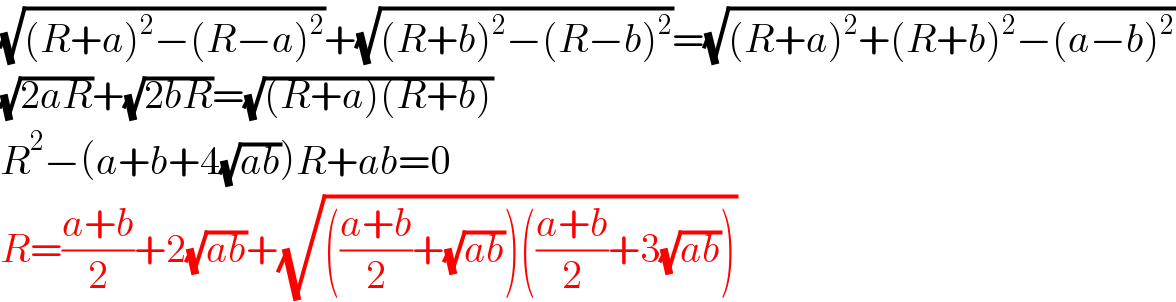
(√((R+a)^2 −(R−a)^2 ))+(√((R+b)^2 −(R−b)^2 ))=(√((R+a)^2 +(R+b)^2 −(a−b)^2 )) (√(2aR))+(√(2bR))=(√((R+a)(R+b))) R^2 −(a+b+4(√(ab)))R+ab=0 R=((a+b)/2)+2(√(ab))+(√((((a+b)/2)+(√(ab)))(((a+b)/2)+3(√(ab)))))

$$\sqrt{\left({R}+{a}\right)^{\mathrm{2}} −\left({R}−{a}\right)^{\mathrm{2}} }+\sqrt{\left({R}+{b}\right)^{\mathrm{2}} −\left({R}−{b}\right)^{\mathrm{2}} }=\sqrt{\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{2}{aR}}+\sqrt{\mathrm{2}{bR}}=\sqrt{\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$${R}^{\mathrm{2}} −\left({a}+{b}+\mathrm{4}\sqrt{{ab}}\right){R}+{ab}=\mathrm{0} \\ $$$${R}=\frac{{a}+{b}}{\mathrm{2}}+\mathrm{2}\sqrt{{ab}}+\sqrt{\left(\frac{{a}+{b}}{\mathrm{2}}+\sqrt{{ab}}\right)\left(\frac{{a}+{b}}{\mathrm{2}}+\mathrm{3}\sqrt{{ab}}\right)} \\ $$

Commented by ajfour last updated on 17/Nov/24

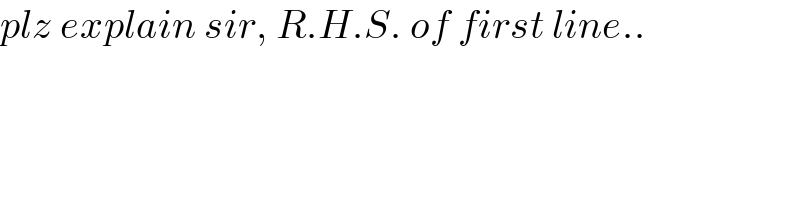
plz explain sir, R.H.S. of first line..

$${plz}\:{explain}\:{sir},\:{R}.{H}.{S}.\:{of}\:{first}\:{line}.. \\ $$

Commented by mr W last updated on 17/Nov/24

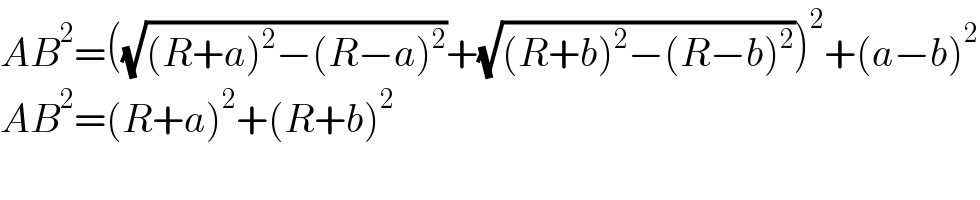
AB^2 =((√((R+a)^2 −(R−a)^2 ))+(√((R+b)^2 −(R−b)^2 )))^2 +(a−b)^2 AB^2 =(R+a)^2 +(R+b)^2

$${AB}^{\mathrm{2}} =\left(\sqrt{\left({R}+{a}\right)^{\mathrm{2}} −\left({R}−{a}\right)^{\mathrm{2}} }+\sqrt{\left({R}+{b}\right)^{\mathrm{2}} −\left({R}−{b}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} +\left({a}−{b}\right)^{\mathrm{2}} \\ $$$${AB}^{\mathrm{2}} =\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} \\ $$

Commented by mr W last updated on 17/Nov/24

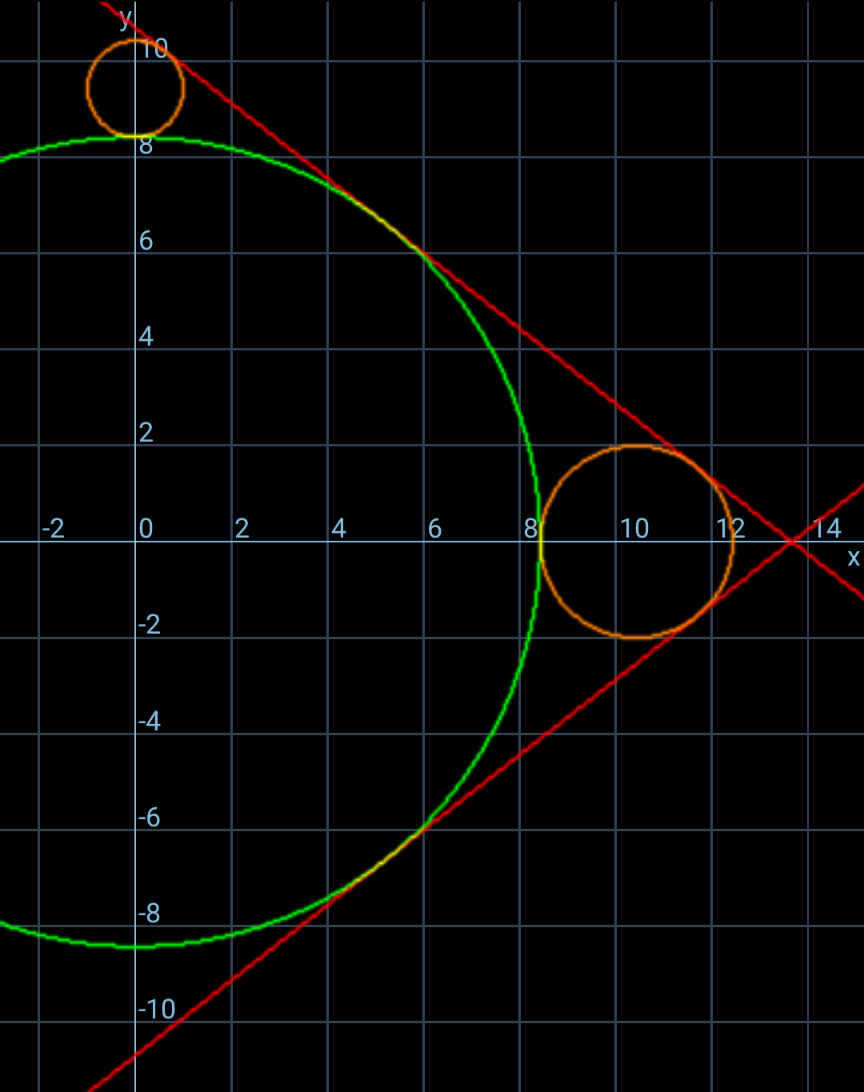
Commented by ajfour last updated on 17/Nov/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com