Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 213803 by muallimRiyoziyot last updated on 17/Nov/24

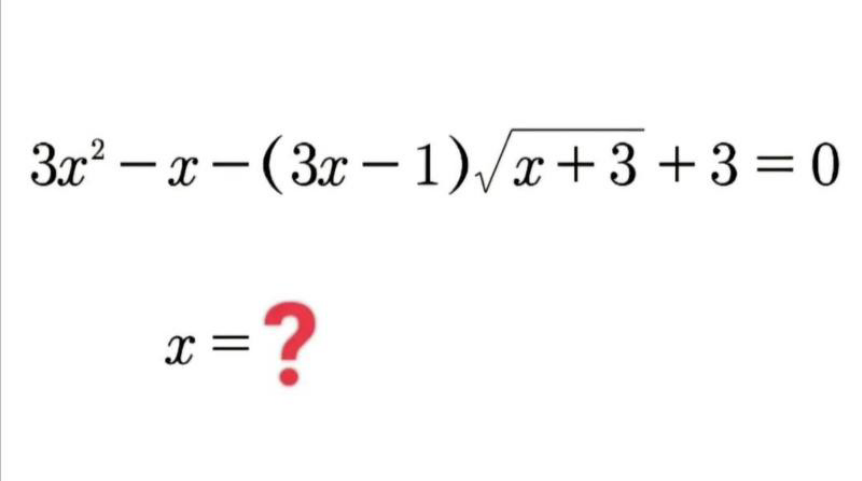
Commented by Frix last updated on 17/Nov/24

There is a pair of complex solutions but the exact form is not useable. x≈1.32848492±.570204126i

$$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{but}\:\mathrm{the} \\ $$$$\mathrm{exact}\:\mathrm{form}\:\mathrm{is}\:\mathrm{not}\:\mathrm{useable}. \\ $$$${x}\approx\mathrm{1}.\mathrm{32848492}\pm.\mathrm{570204126i} \\ $$

Commented by Ghisom last updated on 17/Nov/24

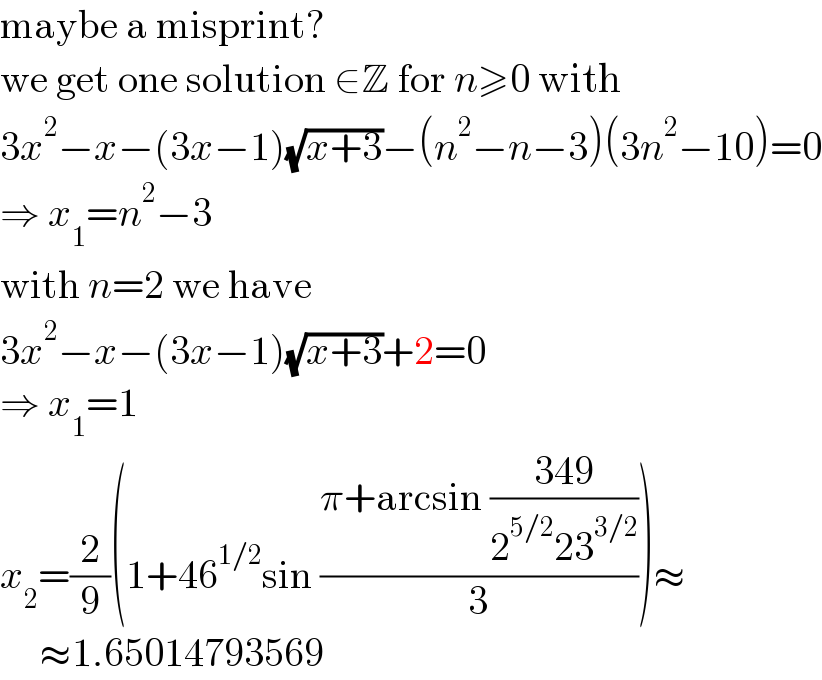
maybe a misprint? we get one solution ∈Z for n≥0 with 3x^2 −x−(3x−1)(√(x+3))−(n^2 −n−3)(3n^2 −10)=0 ⇒ x_1 =n^2 −3 with n=2 we have 3x^2 −x−(3x−1)(√(x+3))+2=0 ⇒ x_1 =1 x_2 =(2/9)(1+46^(1/2) sin ((π+arcsin ((349)/(2^(5/2) 23^(3/2) )))/3))≈ ≈1.65014793569

$$\mathrm{maybe}\:\mathrm{a}\:\mathrm{misprint}? \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{one}\:\mathrm{solution}\:\in\mathbb{Z}\:\mathrm{for}\:{n}\geqslant\mathrm{0}\:\mathrm{with} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −{x}−\left(\mathrm{3}{x}−\mathrm{1}\right)\sqrt{{x}+\mathrm{3}}−\left({n}^{\mathrm{2}} −{n}−\mathrm{3}\right)\left(\mathrm{3}{n}^{\mathrm{2}} −\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} ={n}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{with}\:{n}=\mathrm{2}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −{x}−\left(\mathrm{3}{x}−\mathrm{1}\right)\sqrt{{x}+\mathrm{3}}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{9}}\left(\mathrm{1}+\mathrm{46}^{\mathrm{1}/\mathrm{2}} \mathrm{sin}\:\frac{\pi+\mathrm{arcsin}\:\frac{\mathrm{349}}{\mathrm{2}^{\mathrm{5}/\mathrm{2}} \mathrm{23}^{\mathrm{3}/\mathrm{2}} }}{\mathrm{3}}\right)\approx \\ $$$$\:\:\:\:\:\approx\mathrm{1}.\mathrm{65014793569} \\ $$

Answered by Rasheed.Sindhi last updated on 17/Nov/24

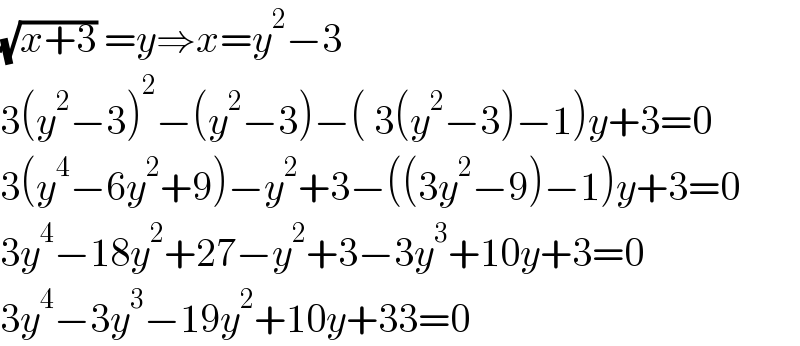
(√(x+3)) =y⇒x=y^2 −3 3(y^2 −3)^2 −(y^2 −3)−( 3(y^2 −3)−1)y+3=0 3(y^4 −6y^2 +9)−y^2 +3−((3y^2 −9)−1)y+3=0 3y^4 −18y^2 +27−y^2 +3−3y^3 +10y+3=0 3y^4 −3y^3 −19y^2 +10y+33=0

$$\sqrt{{x}+\mathrm{3}}\:={y}\Rightarrow{x}={y}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{3}\left({y}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} −\left({y}^{\mathrm{2}} −\mathrm{3}\right)−\left(\:\mathrm{3}\left({y}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{1}\right){y}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}\left({y}^{\mathrm{4}} −\mathrm{6}{y}^{\mathrm{2}} +\mathrm{9}\right)−{y}^{\mathrm{2}} +\mathrm{3}−\left(\left(\mathrm{3}{y}^{\mathrm{2}} −\mathrm{9}\right)−\mathrm{1}\right){y}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{y}^{\mathrm{4}} −\mathrm{18}{y}^{\mathrm{2}} +\mathrm{27}−{y}^{\mathrm{2}} +\mathrm{3}−\mathrm{3}{y}^{\mathrm{3}} +\mathrm{10}{y}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{y}^{\mathrm{4}} −\mathrm{3}{y}^{\mathrm{3}} −\mathrm{19}{y}^{\mathrm{2}} +\mathrm{10}{y}+\mathrm{33}=\mathrm{0} \\ $$

Answered by A5T last updated on 17/Nov/24

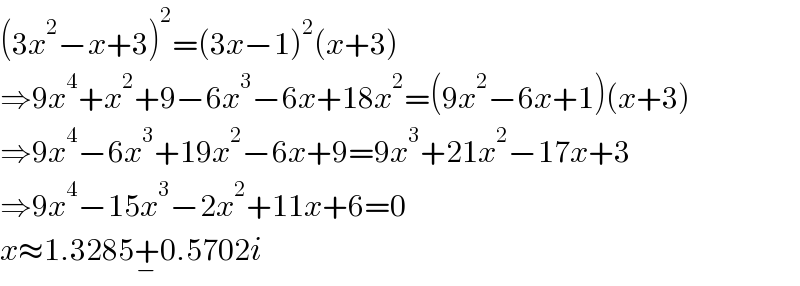
(3x^2 −x+3)^2 =(3x−1)^2 (x+3) ⇒9x^4 +x^2 +9−6x^3 −6x+18x^2 =(9x^2 −6x+1)(x+3) ⇒9x^4 −6x^3 +19x^2 −6x+9=9x^3 +21x^2 −17x+3 ⇒9x^4 −15x^3 −2x^2 +11x+6=0 x≈1.3285+_− 0.5702i

$$\left(\mathrm{3}{x}^{\mathrm{2}} −{x}+\mathrm{3}\right)^{\mathrm{2}} =\left(\mathrm{3}{x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{9}−\mathrm{6}{x}^{\mathrm{3}} −\mathrm{6}{x}+\mathrm{18}{x}^{\mathrm{2}} =\left(\mathrm{9}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{3}} +\mathrm{19}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}=\mathrm{9}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} −\mathrm{17}{x}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{4}} −\mathrm{15}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{6}=\mathrm{0} \\ $$$${x}\approx\mathrm{1}.\mathrm{3285}\underset{−} {+}\mathrm{0}.\mathrm{5702}{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com