Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 213802 by efronzo1 last updated on 17/Nov/24

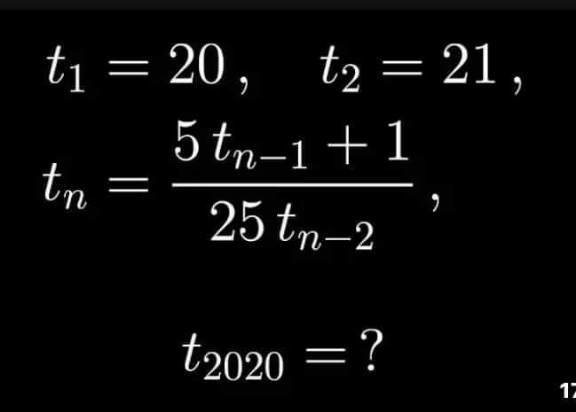
Answered by A5T last updated on 17/Nov/24

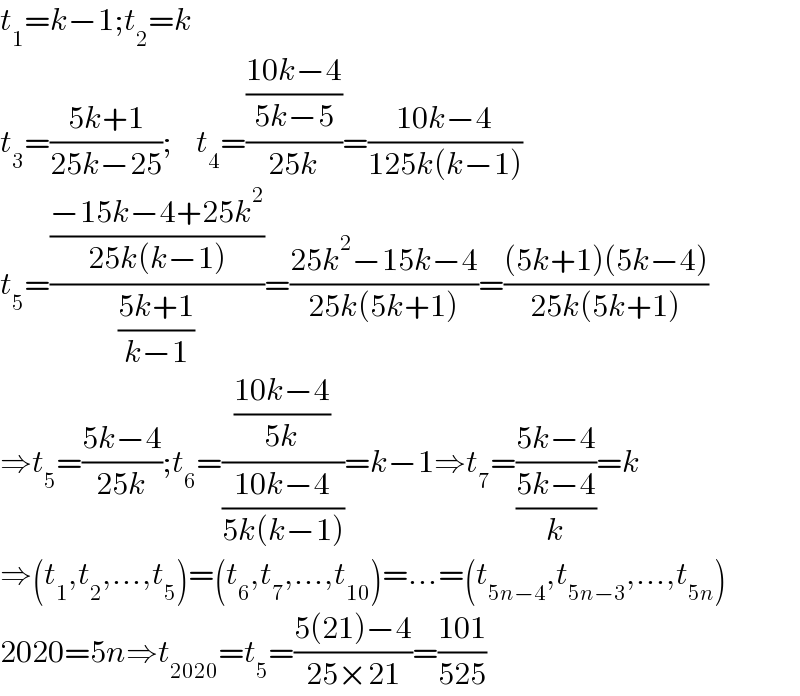
t_1 =k−1;t_2 =k t_3 =((5k+1)/(25k−25)); t_4 =(((10k−4)/(5k−5))/(25k))=((10k−4)/(125k(k−1))) t_5 =(((−15k−4+25k^2 )/(25k(k−1)))/((5k+1)/(k−1)))=((25k^2 −15k−4)/(25k(5k+1)))=(((5k+1)(5k−4))/(25k(5k+1))) ⇒t_5 =((5k−4)/(25k));t_6 =(((10k−4)/(5k))/((10k−4)/(5k(k−1))))=k−1⇒t_7 =((5k−4)/((5k−4)/k))=k ⇒(t_1 ,t_2 ,...,t_5 )=(t_6 ,t_7 ,...,t_(10) )=...=(t_(5n−4) ,t_(5n−3) ,...,t_(5n) ) 2020=5n⇒t_(2020) =t_5 =((5(21)−4)/(25×21))=((101)/(525))

$${t}_{\mathrm{1}} ={k}−\mathrm{1};{t}_{\mathrm{2}} ={k} \\ $$$${t}_{\mathrm{3}} =\frac{\mathrm{5}{k}+\mathrm{1}}{\mathrm{25}{k}−\mathrm{25}};\:\:\:\:{t}_{\mathrm{4}} =\frac{\frac{\mathrm{10}{k}−\mathrm{4}}{\mathrm{5}{k}−\mathrm{5}}}{\mathrm{25}{k}}=\frac{\mathrm{10}{k}−\mathrm{4}}{\mathrm{125}{k}\left({k}−\mathrm{1}\right)} \\ $$$${t}_{\mathrm{5}} =\frac{\frac{−\mathrm{15}{k}−\mathrm{4}+\mathrm{25}{k}^{\mathrm{2}} }{\mathrm{25}{k}\left({k}−\mathrm{1}\right)}}{\frac{\mathrm{5}{k}+\mathrm{1}}{{k}−\mathrm{1}}}=\frac{\mathrm{25}{k}^{\mathrm{2}} −\mathrm{15}{k}−\mathrm{4}}{\mathrm{25}{k}\left(\mathrm{5}{k}+\mathrm{1}\right)}=\frac{\left(\mathrm{5}{k}+\mathrm{1}\right)\left(\mathrm{5}{k}−\mathrm{4}\right)}{\mathrm{25}{k}\left(\mathrm{5}{k}+\mathrm{1}\right)} \\ $$$$\Rightarrow{t}_{\mathrm{5}} =\frac{\mathrm{5}{k}−\mathrm{4}}{\mathrm{25}{k}};{t}_{\mathrm{6}} =\frac{\frac{\mathrm{10}{k}−\mathrm{4}}{\mathrm{5}{k}}}{\frac{\mathrm{10}{k}−\mathrm{4}}{\mathrm{5}{k}\left({k}−\mathrm{1}\right)}}={k}−\mathrm{1}\Rightarrow{t}_{\mathrm{7}} =\frac{\mathrm{5}{k}−\mathrm{4}}{\frac{\mathrm{5}{k}−\mathrm{4}}{{k}}}={k} \\ $$$$\Rightarrow\left({t}_{\mathrm{1}} ,{t}_{\mathrm{2}} ,...,{t}_{\mathrm{5}} \right)=\left({t}_{\mathrm{6}} ,{t}_{\mathrm{7}} ,...,{t}_{\mathrm{10}} \right)=...=\left({t}_{\mathrm{5}{n}−\mathrm{4}} ,{t}_{\mathrm{5}{n}−\mathrm{3}} ,...,{t}_{\mathrm{5}{n}} \right) \\ $$$$\mathrm{2020}=\mathrm{5}{n}\Rightarrow{t}_{\mathrm{2020}} ={t}_{\mathrm{5}} =\frac{\mathrm{5}\left(\mathrm{21}\right)−\mathrm{4}}{\mathrm{25}×\mathrm{21}}=\frac{\mathrm{101}}{\mathrm{525}} \\ $$

Answered by Frix last updated on 17/Nov/24

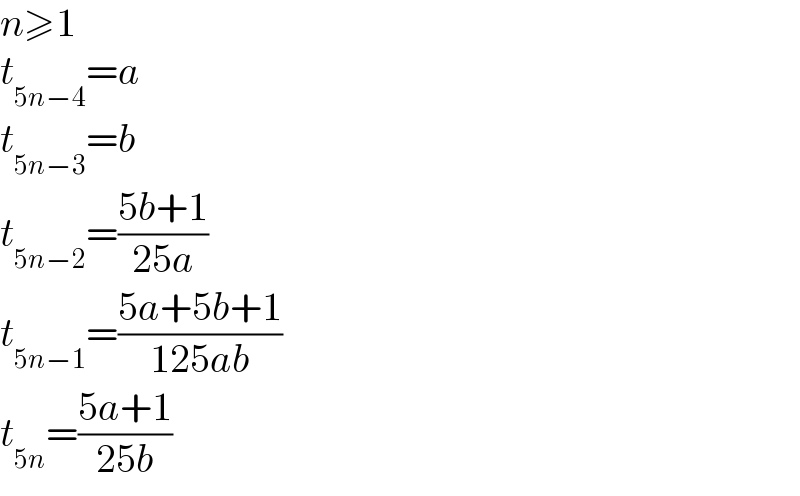
n≥1 t_(5n−4) =a t_(5n−3) =b t_(5n−2) =((5b+1)/(25a)) t_(5n−1) =((5a+5b+1)/(125ab)) t_(5n) =((5a+1)/(25b))

$${n}\geqslant\mathrm{1} \\ $$$${t}_{\mathrm{5}{n}−\mathrm{4}} ={a} \\ $$$${t}_{\mathrm{5}{n}−\mathrm{3}} ={b} \\ $$$${t}_{\mathrm{5}{n}−\mathrm{2}} =\frac{\mathrm{5}{b}+\mathrm{1}}{\mathrm{25}{a}} \\ $$$${t}_{\mathrm{5}{n}−\mathrm{1}} =\frac{\mathrm{5}{a}+\mathrm{5}{b}+\mathrm{1}}{\mathrm{125}{ab}} \\ $$$${t}_{\mathrm{5}{n}} =\frac{\mathrm{5}{a}+\mathrm{1}}{\mathrm{25}{b}} \\ $$

Answered by golsendro last updated on 17/Nov/24

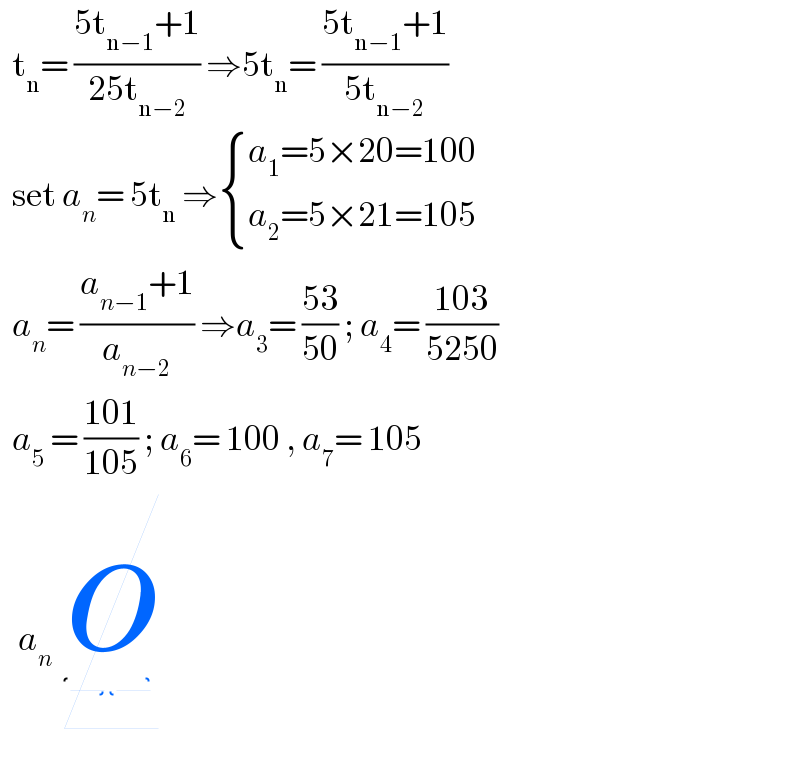
t_n = ((5t_(n−1) +1)/(25t_(n−2) )) ⇒5t_n = ((5t_(n−1) +1)/(5t_(n−2) )) set a_n = 5t_n ⇒ { ((a_1 =5×20=100)),((a_2 =5×21=105)) :} a_n = ((a_(n−1) +1)/a_(n−2) ) ⇒a_3 = ((53)/(50)) ; a_4 = ((103)/(5250)) a_5 = ((101)/(105)) ; a_6 = 100 , a_7 = 105 a_n o

$$\:\:\mathrm{t}_{\mathrm{n}} =\:\frac{\mathrm{5t}_{\mathrm{n}−\mathrm{1}} +\mathrm{1}}{\mathrm{25t}_{\mathrm{n}−\mathrm{2}} }\:\Rightarrow\mathrm{5t}_{\mathrm{n}} =\:\frac{\mathrm{5t}_{\mathrm{n}−\mathrm{1}} +\mathrm{1}}{\mathrm{5t}_{\mathrm{n}−\mathrm{2}} } \\ $$$$\:\:\mathrm{set}\:{a}_{{n}} =\:\mathrm{5t}_{\mathrm{n}} \:\Rightarrow\begin{cases}{{a}_{\mathrm{1}} =\mathrm{5}×\mathrm{20}=\mathrm{100}}\\{{a}_{\mathrm{2}} =\mathrm{5}×\mathrm{21}=\mathrm{105}}\end{cases} \\ $$$$\:\:{a}_{{n}} =\:\frac{{a}_{{n}−\mathrm{1}} +\mathrm{1}}{{a}_{{n}−\mathrm{2}} }\:\Rightarrow{a}_{\mathrm{3}} =\:\frac{\mathrm{53}}{\mathrm{50}}\:;\:{a}_{\mathrm{4}} =\:\frac{\mathrm{103}}{\mathrm{5250}} \\ $$$$\:\:{a}_{\mathrm{5}} \:=\:\frac{\mathrm{101}}{\mathrm{105}}\:;\:{a}_{\mathrm{6}} =\:\mathrm{100}\:,\:{a}_{\mathrm{7}} =\:\mathrm{105} \\ $$$$\:\:\:{a}_{{n}} \:\:\cancel{\underline{\underbrace{{o}}}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com