Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 213797 by efronzo1 last updated on 17/Nov/24

Answered by Frix last updated on 17/Nov/24

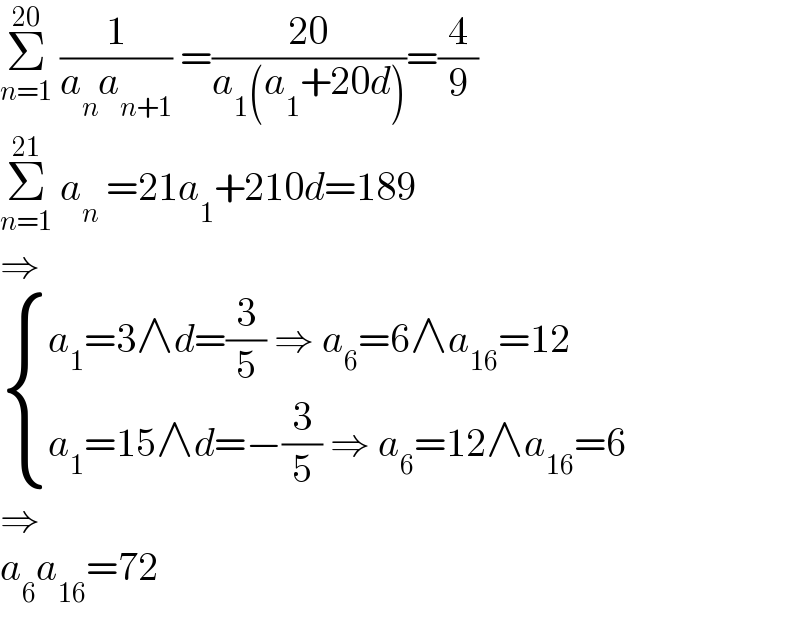
Σ_(n=1) ^(20) (1/(a_n a_(n+1) )) =((20)/(a_1 (a_1 +20d)))=(4/9) Σ_(n=1) ^(21) a_n =21a_1 +210d=189 ⇒ { ((a_1 =3∧d=(3/5) ⇒ a_6 =6∧a_(16) =12)),((a_1 =15∧d=−(3/5) ⇒ a_6 =12∧a_(16) =6)) :} ⇒ a_6 a_(16) =72

$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\:\frac{\mathrm{1}}{{a}_{{n}} {a}_{{n}+\mathrm{1}} }\:=\frac{\mathrm{20}}{{a}_{\mathrm{1}} \left({a}_{\mathrm{1}} +\mathrm{20}{d}\right)}=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{21}} {\sum}}\:{a}_{{n}} \:=\mathrm{21}{a}_{\mathrm{1}} +\mathrm{210}{d}=\mathrm{189} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{a}_{\mathrm{1}} =\mathrm{3}\wedge{d}=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\:{a}_{\mathrm{6}} =\mathrm{6}\wedge{a}_{\mathrm{16}} =\mathrm{12}}\\{{a}_{\mathrm{1}} =\mathrm{15}\wedge{d}=−\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\:{a}_{\mathrm{6}} =\mathrm{12}\wedge{a}_{\mathrm{16}} =\mathrm{6}}\end{cases} \\ $$$$\Rightarrow \\ $$$${a}_{\mathrm{6}} {a}_{\mathrm{16}} =\mathrm{72} \\ $$

Commented by efronzo1 last updated on 17/Nov/24

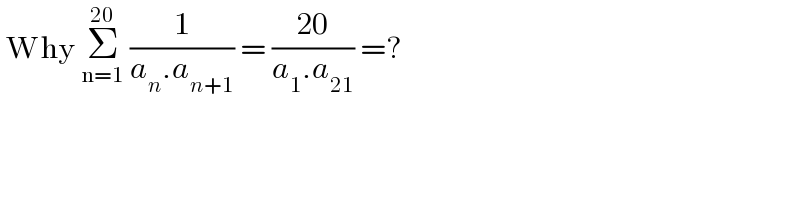
Why Σ_(n=1) ^(20) (1/(a_n .a_(n+1) )) = ((20)/(a_1 .a_(21) )) =?

$$\:\mathrm{Why}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\:\frac{\mathrm{1}}{{a}_{{n}} .{a}_{{n}+\mathrm{1}} }\:=\:\frac{\mathrm{20}}{{a}_{\mathrm{1}} .{a}_{\mathrm{21}} }\:=? \\ $$

Commented by mehdee7396 last updated on 17/Nov/24

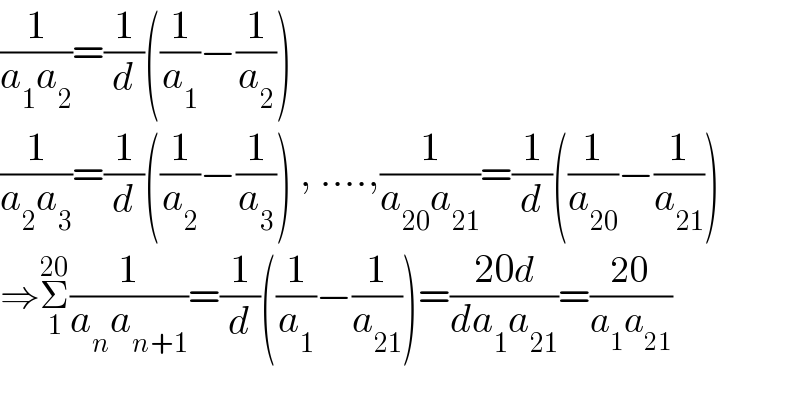
(1/(a_1 a_2 ))=(1/d)((1/a_1 )−(1/a_2 )) (1/(a_2 a_3 ))=(1/d)((1/a_2 )−(1/a_3 )) , ....,(1/(a_(20) a_(21) ))=(1/d)((1/a_(20) )−(1/a_(21) )) ⇒Σ_1 ^(20) (1/(a_n a_(n+1) ))=(1/d)((1/a_1 )−(1/a_(21) ))=((20d)/(da_1 a_(21) ))=((20)/(a_1 a_(21) ))

$$\frac{\mathrm{1}}{{a}_{\mathrm{1}} {a}_{\mathrm{2}} }=\frac{\mathrm{1}}{{d}}\left(\frac{\mathrm{1}}{{a}_{\mathrm{1}} }−\frac{\mathrm{1}}{{a}_{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{1}}{{a}_{\mathrm{2}} {a}_{\mathrm{3}} }=\frac{\mathrm{1}}{{d}}\left(\frac{\mathrm{1}}{{a}_{\mathrm{2}} }−\frac{\mathrm{1}}{{a}_{\mathrm{3}} }\right)\:,\:....,\frac{\mathrm{1}}{{a}_{\mathrm{20}} {a}_{\mathrm{21}} }=\frac{\mathrm{1}}{{d}}\left(\frac{\mathrm{1}}{{a}_{\mathrm{20}} }−\frac{\mathrm{1}}{{a}_{\mathrm{21}} }\right) \\ $$$$\Rightarrow\underset{\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\frac{\mathrm{1}}{{a}_{{n}} {a}_{{n}+\mathrm{1}} }=\frac{\mathrm{1}}{{d}}\left(\frac{\mathrm{1}}{{a}_{\mathrm{1}} }−\frac{\mathrm{1}}{{a}_{\mathrm{21}} }\right)=\frac{\mathrm{20}{d}}{{da}_{\mathrm{1}} {a}_{\mathrm{21}} }=\frac{\mathrm{20}}{{a}_{\mathrm{1}} {a}_{\mathrm{21}} } \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com