Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 213796 by efronzo1 last updated on 17/Nov/24

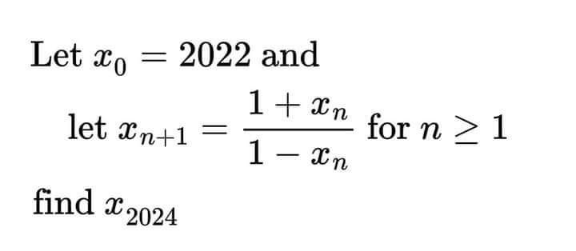
Answered by A5T last updated on 17/Nov/24

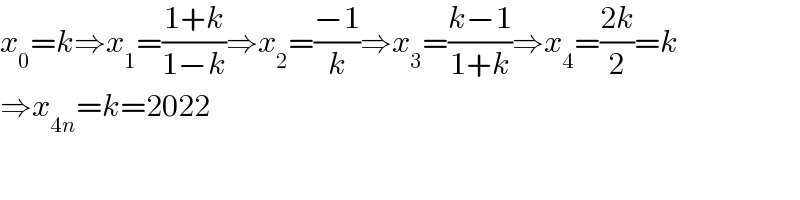
x_0 =k⇒x_1 =((1+k)/(1−k))⇒x_2 =((−1)/k)⇒x_3 =((k−1)/(1+k))⇒x_4 =((2k)/2)=k ⇒x_(4n) =k=2022

$${x}_{\mathrm{0}} ={k}\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+{k}}{\mathrm{1}−{k}}\Rightarrow{x}_{\mathrm{2}} =\frac{−\mathrm{1}}{{k}}\Rightarrow{x}_{\mathrm{3}} =\frac{{k}−\mathrm{1}}{\mathrm{1}+{k}}\Rightarrow{x}_{\mathrm{4}} =\frac{\mathrm{2}{k}}{\mathrm{2}}={k} \\ $$$$\Rightarrow{x}_{\mathrm{4}{n}} ={k}=\mathrm{2022} \\ $$

Answered by Frix last updated on 17/Nov/24

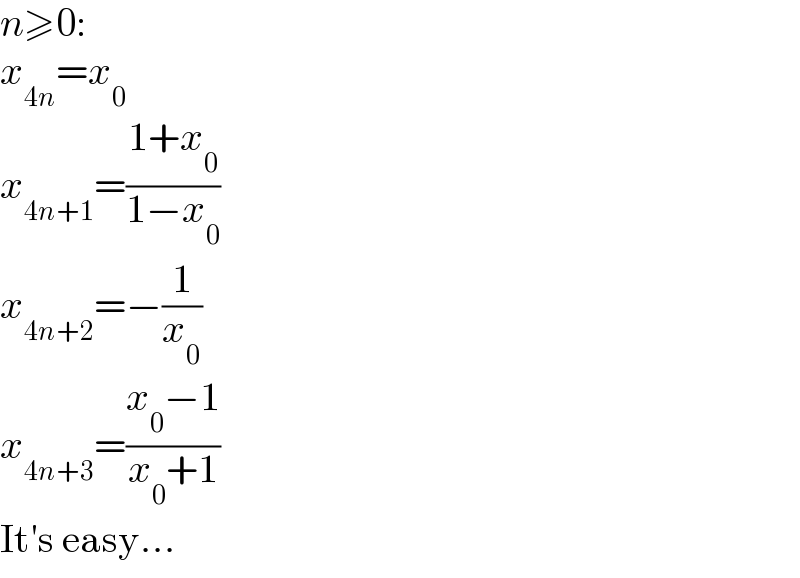
n≥0: x_(4n) =x_0 x_(4n+1) =((1+x_0 )/(1−x_0 )) x_(4n+2) =−(1/x_0 ) x_(4n+3) =((x_0 −1)/(x_0 +1)) It′s easy...

$${n}\geqslant\mathrm{0}: \\ $$$${x}_{\mathrm{4}{n}} ={x}_{\mathrm{0}} \\ $$$${x}_{\mathrm{4}{n}+\mathrm{1}} =\frac{\mathrm{1}+{x}_{\mathrm{0}} }{\mathrm{1}−{x}_{\mathrm{0}} } \\ $$$${x}_{\mathrm{4}{n}+\mathrm{2}} =−\frac{\mathrm{1}}{{x}_{\mathrm{0}} } \\ $$$${x}_{\mathrm{4}{n}+\mathrm{3}} =\frac{{x}_{\mathrm{0}} −\mathrm{1}}{{x}_{\mathrm{0}} +\mathrm{1}} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{easy}... \\ $$

Answered by golsendro last updated on 17/Nov/24

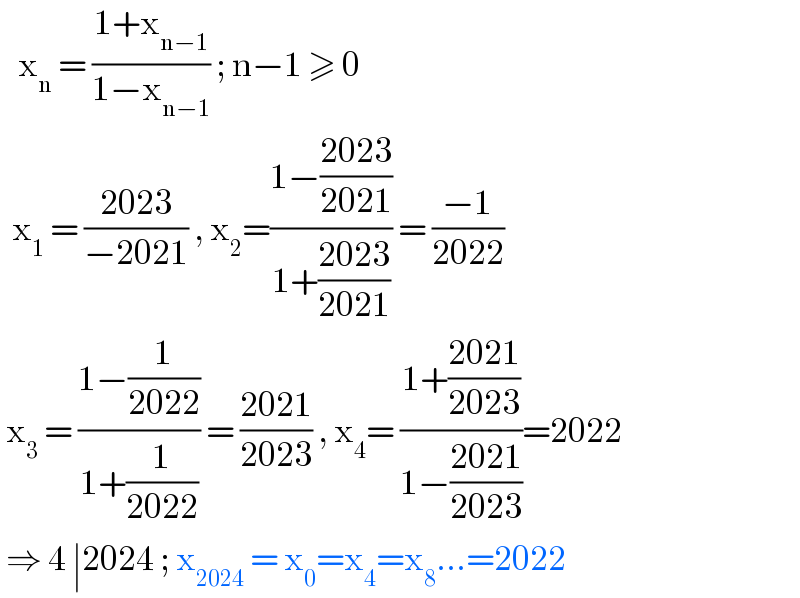
x_n = ((1+x_(n−1) )/(1−x_(n−1) )) ; n−1 ≥ 0 x_1 = ((2023)/(−2021)) , x_2 =((1−((2023)/(2021)))/(1+((2023)/(2021)))) = ((−1)/(2022)) x_3 = ((1−(1/(2022)))/(1+(1/(2022)))) = ((2021)/(2023)) , x_4 = ((1+((2021)/(2023)))/(1−((2021)/(2023))))=2022 ⇒ 4 ∣2024 ; x_(2024) = x_0 =x_4 =x_8 ...=2022

$$\:\:\:\mathrm{x}_{\mathrm{n}} \:=\:\frac{\mathrm{1}+\mathrm{x}_{\mathrm{n}−\mathrm{1}} }{\mathrm{1}−\mathrm{x}_{\mathrm{n}−\mathrm{1}} }\:;\:\mathrm{n}−\mathrm{1}\:\geqslant\:\mathrm{0} \\ $$$$\:\:\mathrm{x}_{\mathrm{1}} \:=\:\frac{\mathrm{2023}}{−\mathrm{2021}}\:,\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{1}−\frac{\mathrm{2023}}{\mathrm{2021}}}{\mathrm{1}+\frac{\mathrm{2023}}{\mathrm{2021}}}\:=\:\frac{−\mathrm{1}}{\mathrm{2022}} \\ $$$$\:\mathrm{x}_{\mathrm{3}} \:=\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2022}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2022}}}\:=\:\frac{\mathrm{2021}}{\mathrm{2023}}\:,\:\mathrm{x}_{\mathrm{4}} =\:\frac{\mathrm{1}+\frac{\mathrm{2021}}{\mathrm{2023}}}{\mathrm{1}−\frac{\mathrm{2021}}{\mathrm{2023}}}=\mathrm{2022} \\ $$$$\:\Rightarrow\:\mathrm{4}\:\mid\mathrm{2024}\:;\:\mathrm{x}_{\mathrm{2024}} \:=\:\mathrm{x}_{\mathrm{0}} =\mathrm{x}_{\mathrm{4}} =\mathrm{x}_{\mathrm{8}} ...=\mathrm{2022} \\ $$

Answered by mr W last updated on 17/Nov/24

let x_n =tan θ_n tan θ_(n+1) =x_(n+1) =((1+tan θ_n )/(1−tan θ_n ))=tan (θ_n +(π/4)) ⇒θ_(n+1) =θ_n +(π/4) ⇒θ_n =θ_(n−1) +(π/4)=θ_(n−2) +((2π)/4)=...=θ_0 +((nπ)/4) ⇒x_n =tan (θ_0 +((nπ)/4))=((tan θ_0 +tan ((nπ)/4))/(1−tan θ_n tan ((nπ)/4))) ⇒x_n =((x_0 +tan ((nπ)/4))/(1−x_0 tan ((nπ)/4)))=((2022+tan ((nπ)/4))/(1−2022 tan ((nπ)/4))) x_(2024) =((2022+tan ((2024π)/4))/(1−2022 tan ((2024π)/4))) =((2022+0)/(1−2022×0))=2022

$${let}\:{x}_{{n}} =\mathrm{tan}\:\theta_{{n}} \\ $$$$\mathrm{tan}\:\theta_{{n}+\mathrm{1}} ={x}_{{n}+\mathrm{1}} =\frac{\mathrm{1}+\mathrm{tan}\:\theta_{{n}} }{\mathrm{1}−\mathrm{tan}\:\theta_{{n}} }=\mathrm{tan}\:\left(\theta_{{n}} +\frac{\pi}{\mathrm{4}}\right) \\ $$$$\Rightarrow\theta_{{n}+\mathrm{1}} =\theta_{{n}} +\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\theta_{{n}} =\theta_{{n}−\mathrm{1}} +\frac{\pi}{\mathrm{4}}=\theta_{{n}−\mathrm{2}} +\frac{\mathrm{2}\pi}{\mathrm{4}}=...=\theta_{\mathrm{0}} +\frac{{n}\pi}{\mathrm{4}} \\ $$$$\Rightarrow{x}_{{n}} =\mathrm{tan}\:\left(\theta_{\mathrm{0}} +\frac{{n}\pi}{\mathrm{4}}\right)=\frac{\mathrm{tan}\:\theta_{\mathrm{0}} +\mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}}{\mathrm{1}−\mathrm{tan}\:\theta_{{n}} \mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}} \\ $$$$\Rightarrow{x}_{{n}} =\frac{{x}_{\mathrm{0}} +\mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}}{\mathrm{1}−{x}_{\mathrm{0}} \mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}}=\frac{\mathrm{2022}+\mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}}{\mathrm{1}−\mathrm{2022}\:\mathrm{tan}\:\frac{{n}\pi}{\mathrm{4}}} \\ $$$${x}_{\mathrm{2024}} =\frac{\mathrm{2022}+\mathrm{tan}\:\frac{\mathrm{2024}\pi}{\mathrm{4}}}{\mathrm{1}−\mathrm{2022}\:\mathrm{tan}\:\frac{\mathrm{2024}\pi}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2022}+\mathrm{0}}{\mathrm{1}−\mathrm{2022}×\mathrm{0}}=\mathrm{2022} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com