
Question Number 213556 by ajfour last updated on 08/Nov/24
Commented by ajfour last updated on 08/Nov/24

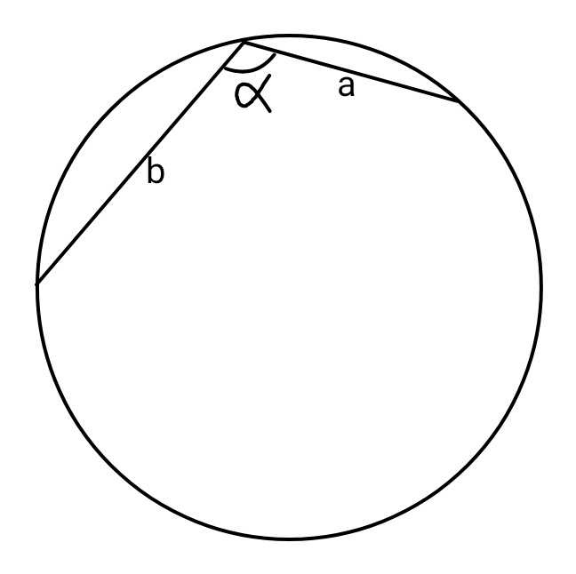
$${Find}\:{radius}. \\ $$
Answered by A5T last updated on 08/Nov/24
![((abc)/(4R))=((absinα)/2)⇒R=(c/(2sinα))[c=(√(a^2 +b^2 −2abcosα))] ⇒R=((√(a^2 +b^2 −2abcosα))/(sinα))](Q213559.png)
$$\frac{{abc}}{\mathrm{4}{R}}=\frac{{absin}\alpha}{\mathrm{2}}\Rightarrow{R}=\frac{{c}}{\mathrm{2}{sin}\alpha}\left[{c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{abcos}\alpha}\right] \\ $$$$\Rightarrow{R}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{abcos}\alpha}}{{sin}\alpha} \\ $$
Answered by mr W last updated on 08/Nov/24
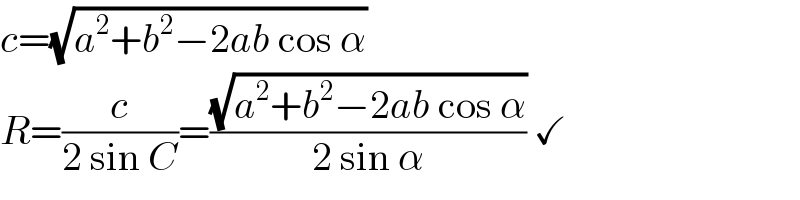
$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\alpha} \\ $$$${R}=\frac{{c}}{\mathrm{2}\:\mathrm{sin}\:{C}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\alpha}}{\mathrm{2}\:\mathrm{sin}\:\alpha}\:\checkmark \\ $$
Commented by ajfour last updated on 08/Nov/24

$${too}\:{good}! \\ $$
Answered by Spillover last updated on 09/Nov/24

