Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 213550 by mr W last updated on 08/Nov/24

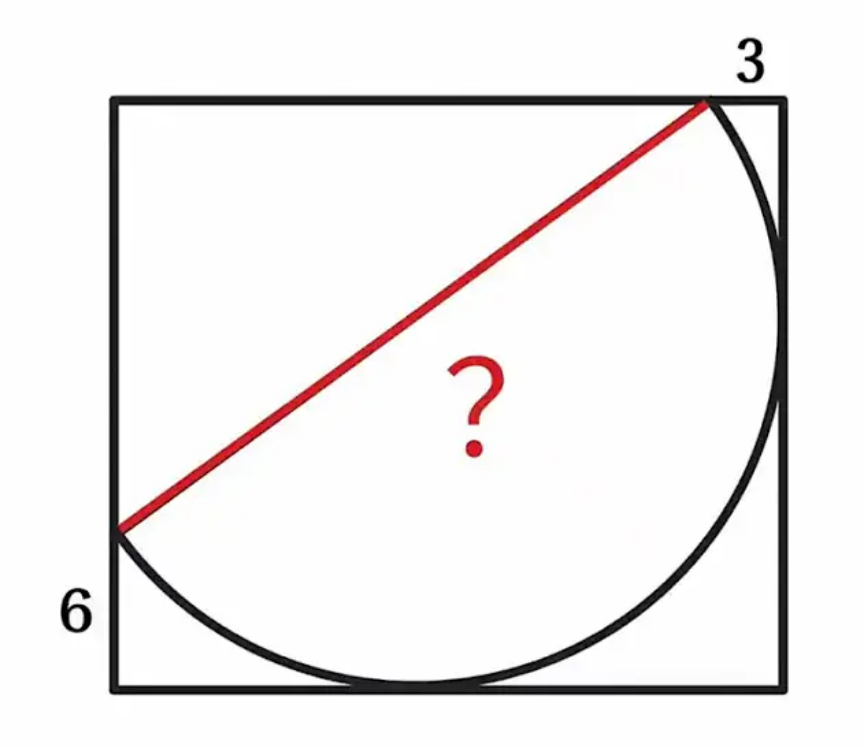
Commented by mr W last updated on 08/Nov/24

semicircle

$${semicircle} \\ $$

Answered by A5T last updated on 08/Nov/24

Commented by A5T last updated on 08/Nov/24

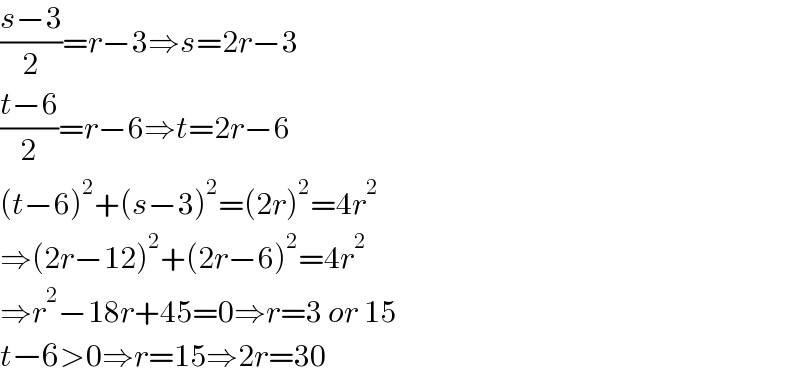
((s−3)/2)=r−3⇒s=2r−3 ((t−6)/2)=r−6⇒t=2r−6 (t−6)^2 +(s−3)^2 =(2r)^2 =4r^2 ⇒(2r−12)^2 +(2r−6)^2 =4r^2 ⇒r^2 −18r+45=0⇒r=3 or 15 t−6>0⇒r=15⇒2r=30

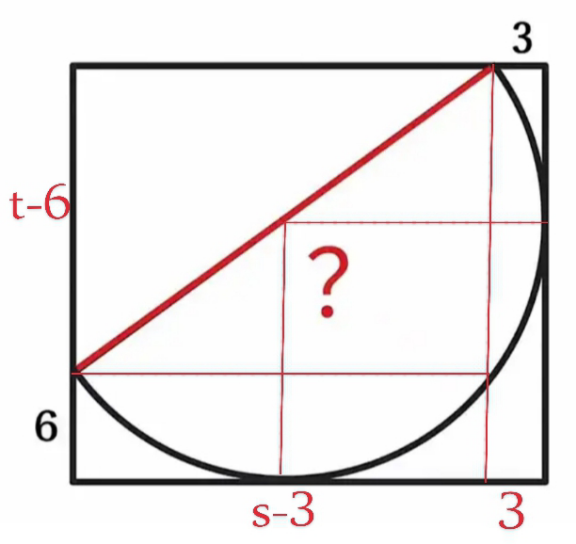
$$\frac{{s}−\mathrm{3}}{\mathrm{2}}={r}−\mathrm{3}\Rightarrow{s}=\mathrm{2}{r}−\mathrm{3} \\ $$$$\frac{{t}−\mathrm{6}}{\mathrm{2}}={r}−\mathrm{6}\Rightarrow{t}=\mathrm{2}{r}−\mathrm{6} \\ $$$$\left({t}−\mathrm{6}\right)^{\mathrm{2}} +\left({s}−\mathrm{3}\right)^{\mathrm{2}} =\left(\mathrm{2}{r}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{r}−\mathrm{12}\right)^{\mathrm{2}} +\left(\mathrm{2}{r}−\mathrm{6}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} −\mathrm{18}{r}+\mathrm{45}=\mathrm{0}\Rightarrow{r}=\mathrm{3}\:{or}\:\mathrm{15} \\ $$$${t}−\mathrm{6}>\mathrm{0}\Rightarrow{r}=\mathrm{15}\Rightarrow\mathrm{2}{r}=\mathrm{30} \\ $$

Commented by mr W last updated on 08/Nov/24

��

Answered by Spillover last updated on 09/Nov/24

R²=[R -6]²+ [R -3]² R² -12R +36 + R² -6R +9 R²=2R² -18R +45 R² -18R +45=0 R=[18+[324 - 180]½]/2 R=[18+12]/2=15 EF=[15+15]=30

$$ \\ $$R²=[R -6]²+ [R -3]² R² -12R +36 + R² -6R +9 R²=2R² -18R +45 R² -18R +45=0 R=[18+[324 - 180]½]/2 R=[18+12]/2=15 EF=[15+15]=30

Terms of Service

Privacy Policy

Contact: info@tinkutara.com