Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

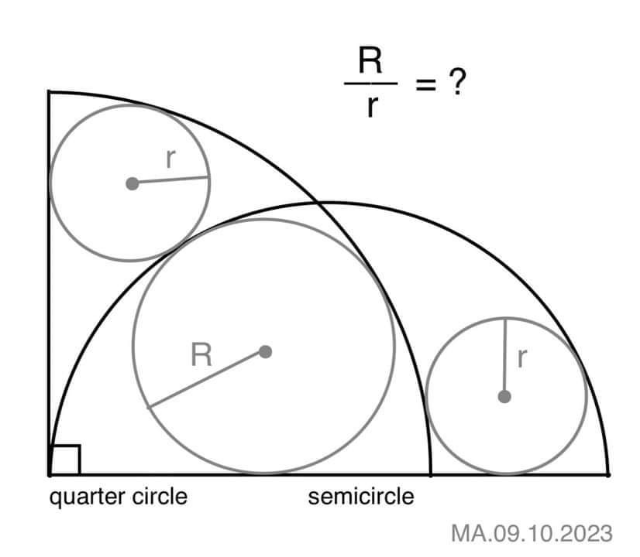
Question Number 213323 by Spillover last updated on 02/Nov/24

Commented by Frix last updated on 03/Nov/24

No nice numbers Let r=1 ⇒ ρ_(q.c.) ≈4.87164313433 [ _(polynome of 8^(th) degree )^(Solution of a) ] ρ_(s.c.) ≈3.49740513991 R≈1.66629777247

$$\mathrm{No}\:\mathrm{nice}\:\mathrm{numbers} \\ $$$$\mathrm{Let}\:{r}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\rho_{{q}.{c}.} \approx\mathrm{4}.\mathrm{87164313433}\:\left[\:_{\mathrm{polynome}\:\mathrm{of}\:\mathrm{8}^{\mathrm{th}} \:\mathrm{degree}\:} ^{\mathrm{Solution}\:\mathrm{of}\:\mathrm{a}} \right] \\ $$$$\rho_{{s}.{c}.} \approx\mathrm{3}.\mathrm{49740513991} \\ $$$${R}\approx\mathrm{1}.\mathrm{66629777247} \\ $$

Answered by mr W last updated on 03/Nov/24

Commented by mr W last updated on 03/Nov/24

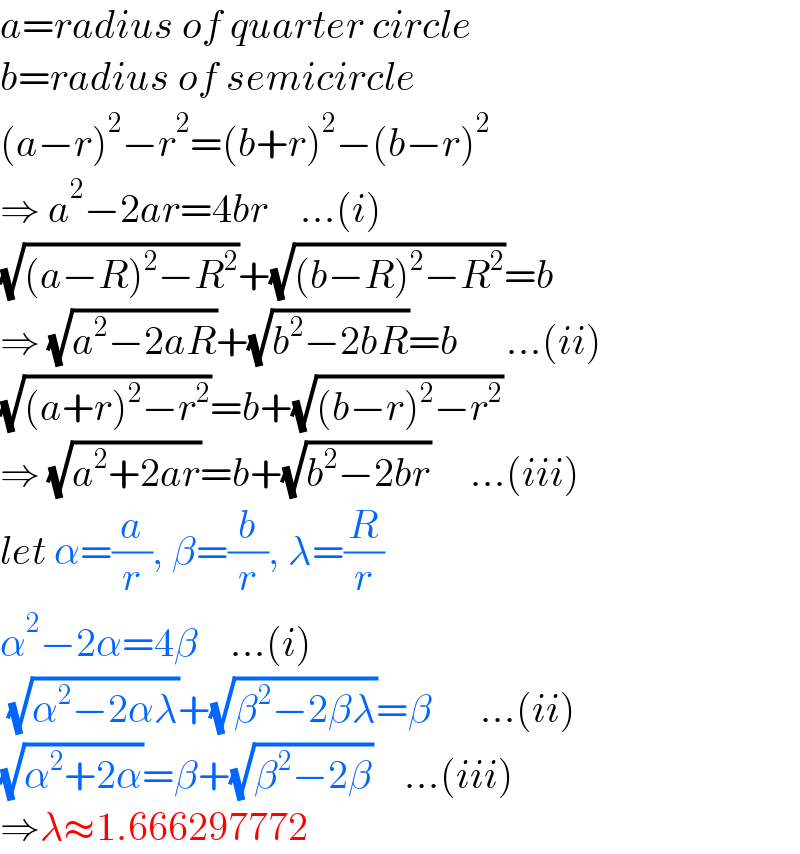
a=radius of quarter circle b=radius of semicircle (a−r)^2 −r^2 =(b+r)^2 −(b−r)^2 ⇒ a^2 −2ar=4br ...(i) (√((a−R)^2 −R^2 ))+(√((b−R)^2 −R^2 ))=b ⇒ (√(a^2 −2aR))+(√(b^2 −2bR))=b ...(ii) (√((a+r)^2 −r^2 ))=b+(√((b−r)^2 −r^2 )) ⇒ (√(a^2 +2ar))=b+(√(b^2 −2br)) ...(iii) let α=(a/r), β=(b/r), λ=(R/r) α^2 −2α=4β ...(i) (√(α^2 −2αλ))+(√(β^2 −2βλ))=β ...(ii) (√(α^2 +2α))=β+(√(β^2 −2β)) ...(iii) ⇒λ≈1.666297772

$${a}={radius}\:{of}\:{quarter}\:{circle} \\ $$$${b}={radius}\:{of}\:{semicircle} \\ $$$$\left({a}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\left({b}+{r}\right)^{\mathrm{2}} −\left({b}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} −\mathrm{2}{ar}=\mathrm{4}{br}\:\:\:\:...\left({i}\right) \\ $$$$\sqrt{\left({a}−{R}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }+\sqrt{\left({b}−{R}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }={b} \\ $$$$\Rightarrow\:\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{aR}}+\sqrt{{b}^{\mathrm{2}} −\mathrm{2}{bR}}={b}\:\:\:\:\:\:...\left({ii}\right) \\ $$$$\sqrt{\left({a}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }={b}+\sqrt{\left({b}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ar}}={b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{2}{br}}\:\:\:\:\:...\left({iii}\right) \\ $$$${let}\:\alpha=\frac{{a}}{{r}},\:\beta=\frac{{b}}{{r}},\:\lambda=\frac{{R}}{{r}} \\ $$$$\alpha^{\mathrm{2}} −\mathrm{2}\alpha=\mathrm{4}\beta\:\:\:\:...\left({i}\right) \\ $$$$\:\sqrt{\alpha^{\mathrm{2}} −\mathrm{2}\alpha\lambda}+\sqrt{\beta^{\mathrm{2}} −\mathrm{2}\beta\lambda}=\beta\:\:\:\:\:\:...\left({ii}\right) \\ $$$$\sqrt{\alpha^{\mathrm{2}} +\mathrm{2}\alpha}=\beta+\sqrt{\beta^{\mathrm{2}} −\mathrm{2}\beta}\:\:\:\:...\left({iii}\right) \\ $$$$\Rightarrow\lambda\approx\mathrm{1}.\mathrm{666297772} \\ $$

Commented by Spillover last updated on 03/Nov/24

perfect

$${perfect} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com