Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

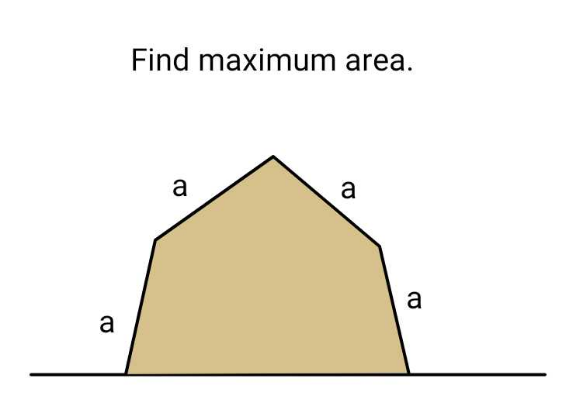
Question Number 213250 by ajfour last updated on 01/Nov/24

Answered by a.lgnaoui last updated on 02/Nov/24

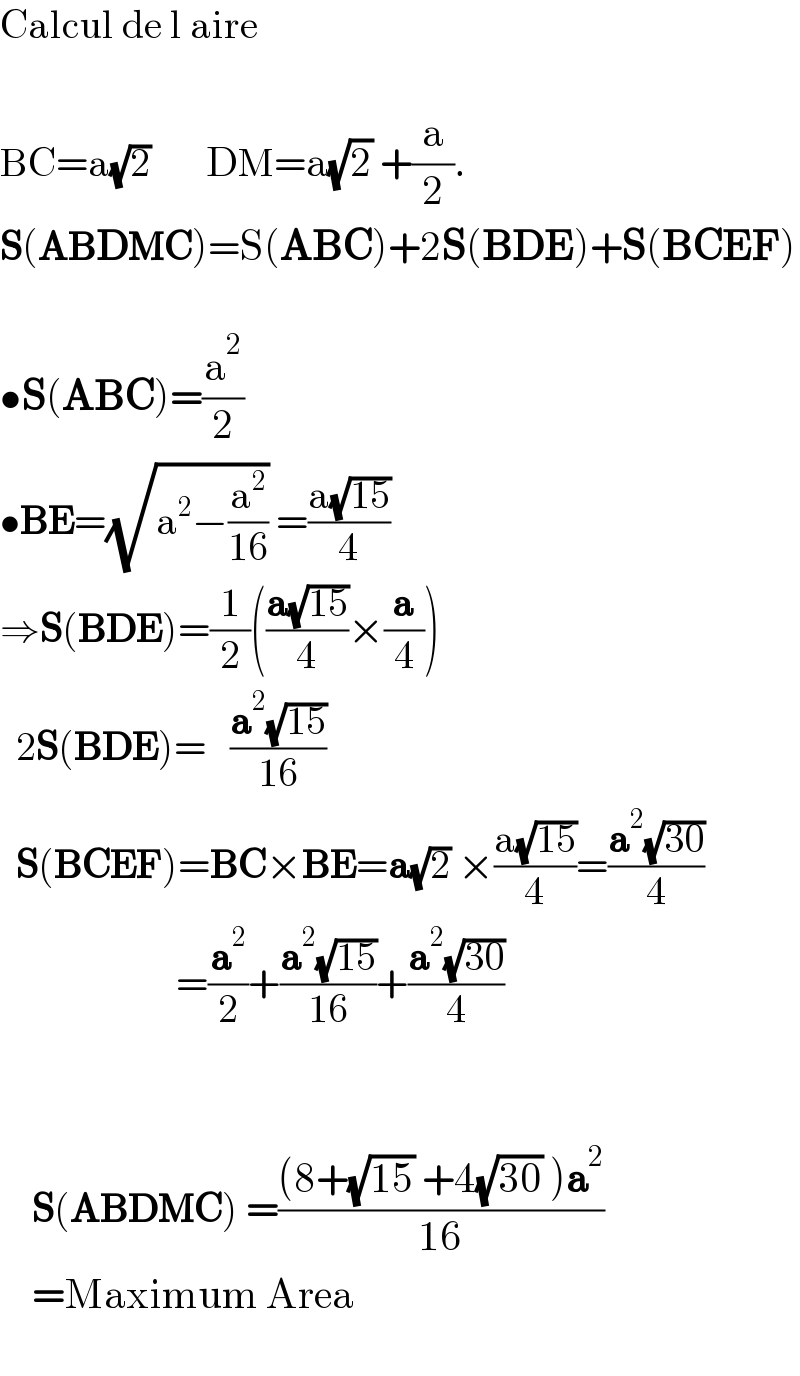
Calcul de l aire BC=a(√2) DM=a(√2) +(a/2). S(ABDMC)=S(ABC)+2S(BDE)+S(BCEF) •S(ABC)=(a^2 /2) •BE=(√(a^2 −(a^2 /(16)))) =((a(√(15)))/4) ⇒S(BDE)=(1/2)(((a(√(15)))/4)×(a/4)) 2S(BDE)= ((a^2 (√(15)))/(16)) S(BCEF)=BC×BE=a(√2) ×((a(√(15)))/4)=((a^2 (√(30)))/4) =(a^2 /2)+((a^2 (√(15)))/(16))+((a^2 (√(30)))/4) S(ABDMC) =(((8+(√(15)) +4(√(30)) )a^2 )/(16)) =Maximum Area

$$\mathrm{Calcul}\:\mathrm{de}\:\mathrm{l}\:\mathrm{aire} \\ $$$$ \\ $$$$\mathrm{BC}=\mathrm{a}\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\mathrm{DM}=\mathrm{a}\sqrt{\mathrm{2}}\:+\frac{\mathrm{a}}{\mathrm{2}}. \\ $$$$\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{ABDMC}}\right)=\mathrm{S}\left(\boldsymbol{\mathrm{ABC}}\right)+\mathrm{2}\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{BDE}}\right)+\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{BCEF}}\right) \\ $$$$ \\ $$$$\bullet\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{ABC}}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\:\:\:\: \\ $$$$\bullet\boldsymbol{\mathrm{BE}}=\sqrt{\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{16}}}\:=\frac{\mathrm{a}\sqrt{\mathrm{15}}}{\mathrm{4}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{BDE}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\boldsymbol{\mathrm{a}}\sqrt{\mathrm{15}}}{\mathrm{4}}×\frac{\boldsymbol{\mathrm{a}}}{\mathrm{4}}\right) \\ $$$$\:\:\mathrm{2}\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{BDE}}\right)=\:\:\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \sqrt{\mathrm{15}}}{\mathrm{16}} \\ $$$$\:\:\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{BCEF}}\right)=\boldsymbol{\mathrm{BC}}×\boldsymbol{\mathrm{BE}}=\boldsymbol{\mathrm{a}}\sqrt{\mathrm{2}}\:×\frac{\mathrm{a}\sqrt{\mathrm{15}}}{\mathrm{4}}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \sqrt{\mathrm{30}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{2}}+\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \sqrt{\mathrm{15}}}{\mathrm{16}}+\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \sqrt{\mathrm{30}}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{ABDMC}}\right)\:=\frac{\left(\mathrm{8}+\sqrt{\mathrm{15}}\:+\mathrm{4}\sqrt{\mathrm{30}}\:\right)\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\:\:\:\:=\mathrm{Maximum}\:\mathrm{Area} \\ $$$$\:\:\:\:\:\:\: \\ $$

Commented by a.lgnaoui last updated on 02/Nov/24

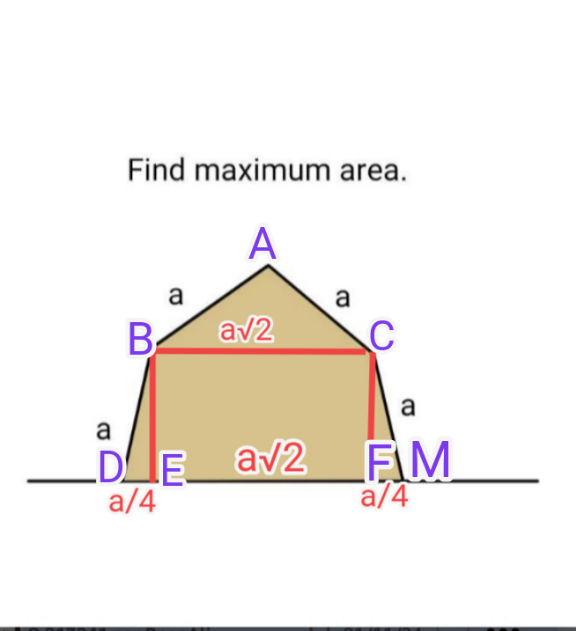
Commented by mr W last updated on 02/Nov/24

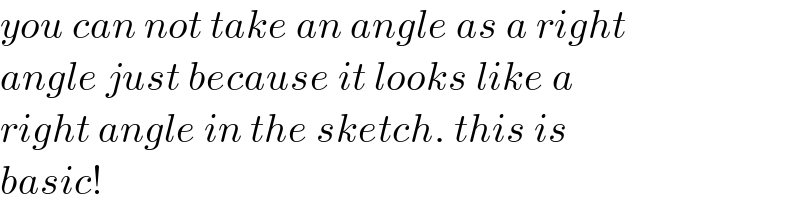
you can not take an angle as a right angle just because it looks like a right angle in the sketch. this is basic!

$${you}\:{can}\:{not}\:{take}\:{an}\:{angle}\:{as}\:{a}\:{right} \\ $$$${angle}\:{just}\:{because}\:{it}\:{looks}\:{like}\:{a} \\ $$$${right}\:{angle}\:{in}\:{the}\:{sketch}.\:{this}\:{is}\: \\ $$$${basic}! \\ $$

Answered by Frix last updated on 02/Nov/24

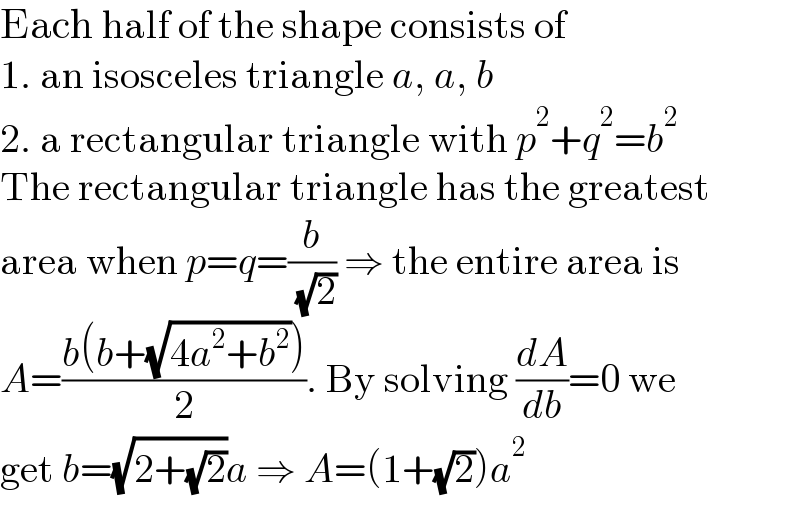
Each half of the shape consists of 1. an isosceles triangle a, a, b 2. a rectangular triangle with p^2 +q^2 =b^2 The rectangular triangle has the greatest area when p=q=(b/( (√2))) ⇒ the entire area is A=((b(b+(√(4a^2 +b^2 ))))/2). By solving (dA/db)=0 we get b=(√(2+(√2)))a ⇒ A=(1+(√2))a^2

$$\mathrm{Each}\:\mathrm{half}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shape}\:\mathrm{consists}\:\mathrm{of} \\ $$$$\mathrm{1}.\:\mathrm{an}\:\mathrm{isosceles}\:\mathrm{triangle}\:{a},\:{a},\:{b} \\ $$$$\mathrm{2}.\:\mathrm{a}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{with}\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{has}\:\mathrm{the}\:\mathrm{greatest} \\ $$$$\mathrm{area}\:\mathrm{when}\:{p}={q}=\frac{{b}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:\mathrm{the}\:\mathrm{entire}\:\mathrm{area}\:\mathrm{is} \\ $$$${A}=\frac{{b}\left({b}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}{\mathrm{2}}.\:\mathrm{By}\:\mathrm{solving}\:\frac{{dA}}{{db}}=\mathrm{0}\:\mathrm{we} \\ $$$$\mathrm{get}\:{b}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}{a}\:\Rightarrow\:{A}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){a}^{\mathrm{2}} \\ $$

Commented by ajfour last updated on 02/Nov/24

very straight and precise! i like it.

$${very}\:{straight}\:{and}\:{precise}!\:{i}\:{like}\:{it}. \\ $$

Commented by Frix last updated on 02/Nov/24

Thank you

$$\mathrm{Thank}\:\mathrm{you} \\ $$

Answered by mr W last updated on 02/Nov/24

Commented by mr W last updated on 02/Nov/24

let′s look at the general case with 4 different sides a,b,c,d. if we image that the wall is a mirror, the question is when the area of an octagon is maximum. the answer is when the octagon is cyclic.

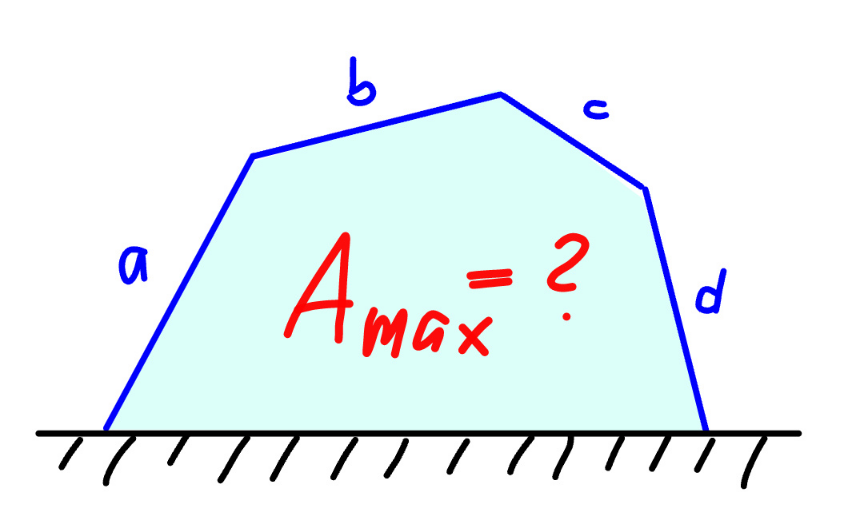
$${let}'{s}\:{look}\:{at}\:{the}\:{general}\:{case}\:{with} \\ $$$$\mathrm{4}\:{different}\:{sides}\:{a},{b},{c},{d}. \\ $$$${if}\:{we}\:{image}\:{that}\:{the}\:{wall}\:{is}\:{a}\:{mirror}, \\ $$$${the}\:{question}\:{is}\:{when}\:{the}\:{area}\:{of}\:{an} \\ $$$${octagon}\:{is}\:{maximum}.\:{the}\:{answer}\:{is} \\ $$$${when}\:{the}\:{octagon}\:{is}\:{cyclic}. \\ $$

Commented by mr W last updated on 02/Nov/24

Commented by mr W last updated on 02/Nov/24

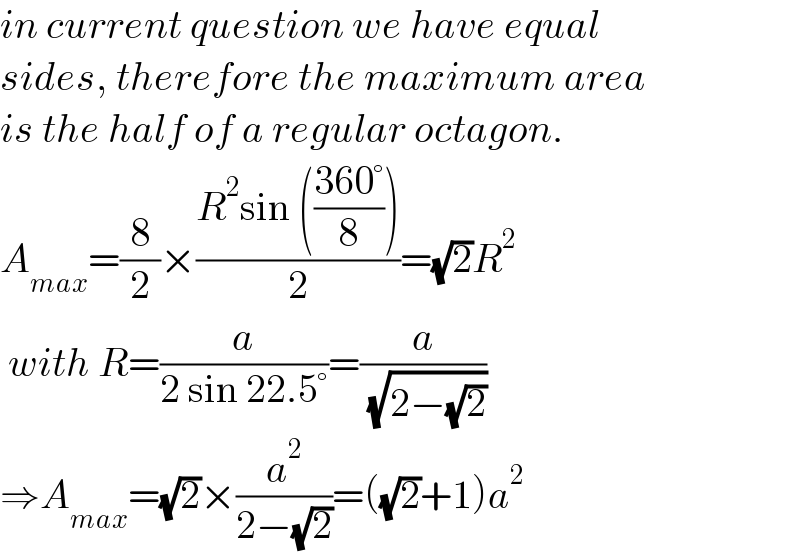
in current question we have equal sides, therefore the maximum area is the half of a regular octagon. A_(max) =(8/2)×((R^2 sin (((360°)/8)))/2)=(√2)R^2 with R=(a/(2 sin 22.5°))=(a/( (√(2−(√2))))) ⇒A_(max) =(√2)×(a^2 /(2−(√2)))=((√2)+1)a^2

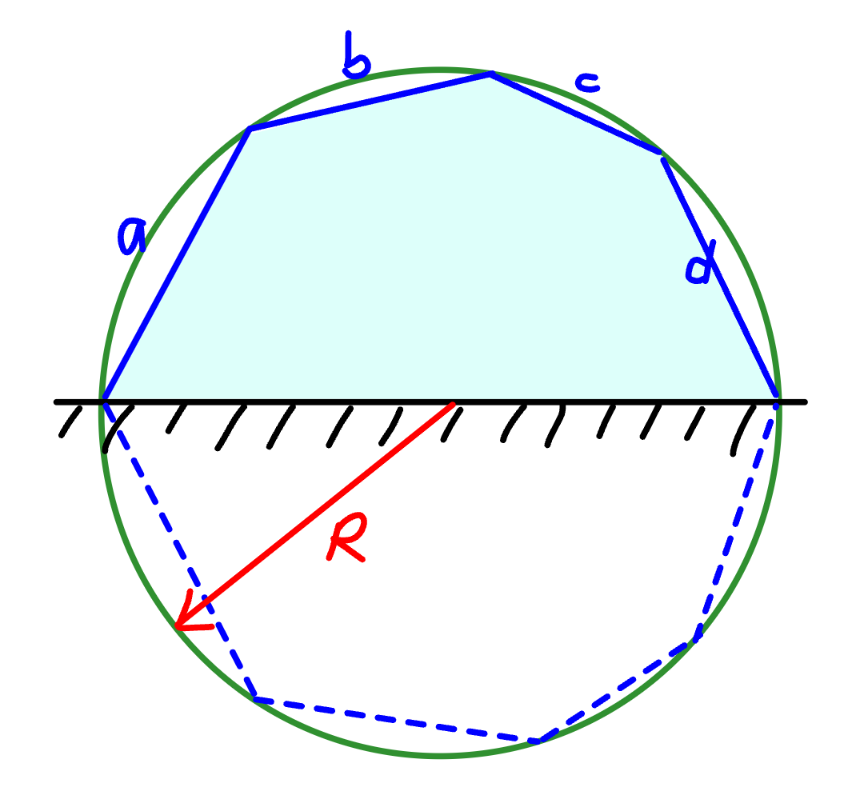
$${in}\:{current}\:{question}\:{we}\:{have}\:{equal} \\ $$$${sides},\:{therefore}\:{the}\:{maximum}\:{area} \\ $$$${is}\:{the}\:{half}\:{of}\:{a}\:{regular}\:{octagon}. \\ $$$${A}_{{max}} =\frac{\mathrm{8}}{\mathrm{2}}×\frac{{R}^{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{360}°}{\mathrm{8}}\right)}{\mathrm{2}}=\sqrt{\mathrm{2}}{R}^{\mathrm{2}} \\ $$$$\:{with}\:{R}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{22}.\mathrm{5}°}=\frac{{a}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}} \\ $$$$\Rightarrow{A}_{{max}} =\sqrt{\mathrm{2}}×\frac{{a}^{\mathrm{2}} }{\mathrm{2}−\sqrt{\mathrm{2}}}=\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){a}^{\mathrm{2}} \\ $$

Commented by ajfour last updated on 02/Nov/24

Utter well thought!

$${Utter}\:{well}\:{thought}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com