Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

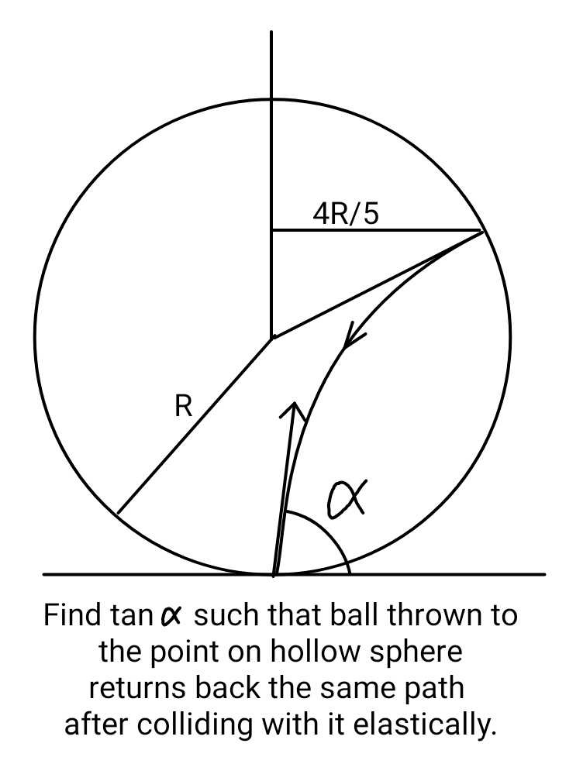
Question Number 213234 by ajfour last updated on 01/Nov/24

Commented by Ghisom last updated on 01/Nov/24

let r=1 P∈circle: P= (((cos θ)),((1+sin θ)) ) parabola: y=(((2+sin θ)/(cos θ))−(x/(cos^2 θ)))x tan α=((2+sin θ)/(cos θ)) with θ=arctan (3/4) we get P= (((4/5)),((8/5)) ) par: y=(((13)/4)−((25)/(16))x)x tan α =((13)/4)

$$\mathrm{let}\:{r}=\mathrm{1} \\ $$$${P}\in\mathrm{circle}:\:{P}=\begin{pmatrix}{\mathrm{cos}\:\theta}\\{\mathrm{1}+\mathrm{sin}\:\theta}\end{pmatrix} \\ $$$$\mathrm{parabola}:\:{y}=\left(\frac{\mathrm{2}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}−\frac{{x}}{\mathrm{cos}^{\mathrm{2}} \:\theta}\right){x} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{2}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$ \\ $$$$\mathrm{with}\:\theta=\mathrm{arctan}\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{we}\:\mathrm{get} \\ $$$${P}=\begin{pmatrix}{\mathrm{4}/\mathrm{5}}\\{\mathrm{8}/\mathrm{5}}\end{pmatrix} \\ $$$$\mathrm{par}:\:{y}=\left(\frac{\mathrm{13}}{\mathrm{4}}−\frac{\mathrm{25}}{\mathrm{16}}{x}\right){x} \\ $$$$\mathrm{tan}\:\alpha\:=\frac{\mathrm{13}}{\mathrm{4}} \\ $$

Commented by mr W last updated on 02/Nov/24

please post your answer as “answer”, not as “comment”.

$${please}\:{post}\:{your}\:{answer}\:{as}\:``{answer}'', \\ $$$${not}\:{as}\:``{comment}''. \\ $$

Answered by a.lgnaoui last updated on 01/Nov/24

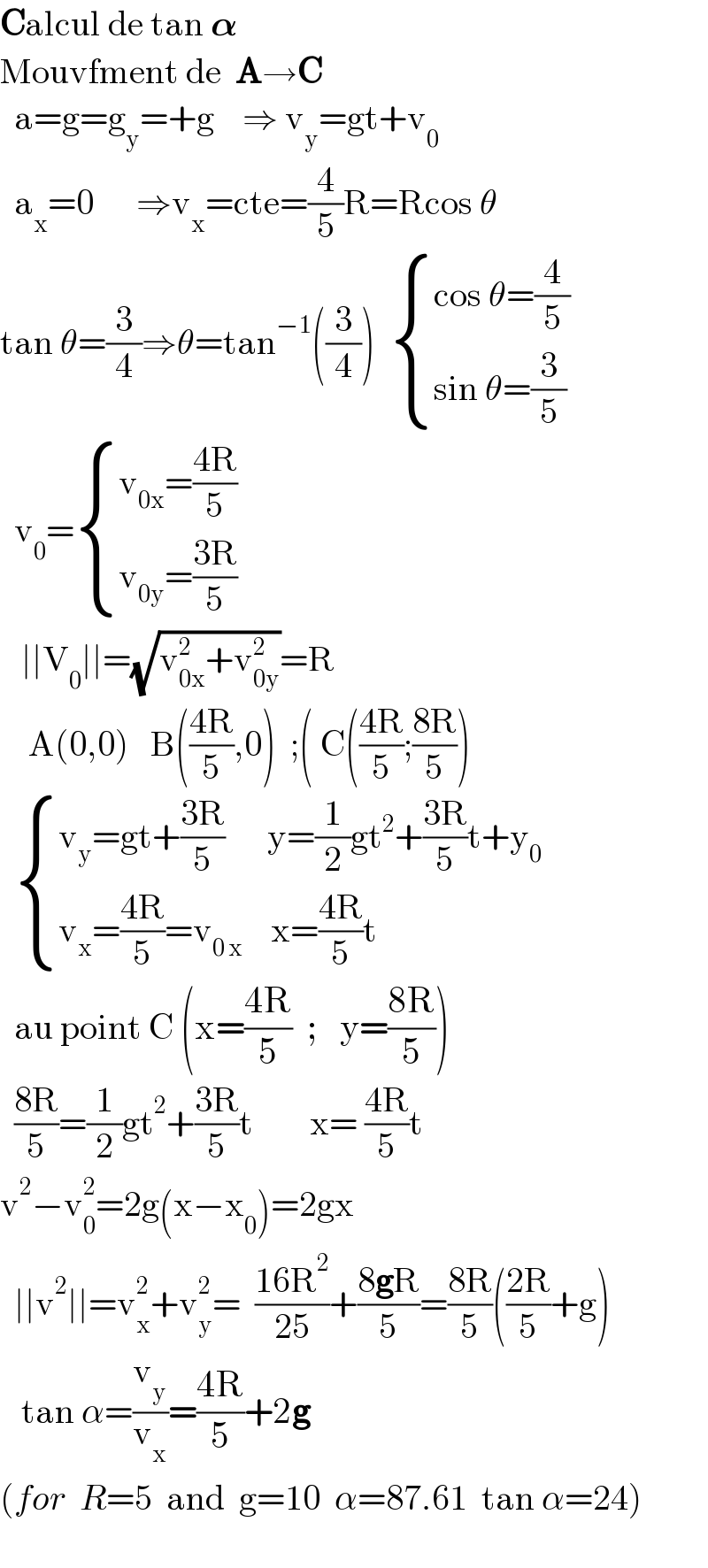
Calcul de tan 𝛂 Mouvfment de A→C a=g=g_y =+g ⇒ v_y =gt+v_0 a_x =0 ⇒v_x =cte=(4/5)R=Rcos θ tan θ=(3/4)⇒θ=tan^(−1) ((3/4)) { ((cos θ=(4/5))),((sin θ=(3/5))) :} v_0 = { ((v_(0x) =((4R)/5))),((v_(0y) =((3R)/5))) :} ∣∣V_0 ∣∣=(√(v_(0x) ^2 +v_(0y) ^2 ))=R A(0,0) B(((4R)/5),0) ;( C(((4R)/5);((8R)/5)) { ((v_y =gt+((3R)/5) y=(1/2)gt^2 +((3R)/5)t+y_0 )),((v_x =((4R)/5)=v_(0 x) x=((4R)/5)t)) :} au point C (x=((4R)/5) ; y=((8R)/5)) ((8R)/5)=(1/2)gt^2 +((3R)/5)t x= ((4R)/5)t v^2 −v_0 ^2 =2g(x−x_0 )=2gx ∣∣v^2 ∣∣=v_x ^2 +v_y ^2 = ((16R^2 )/(25))+((8gR)/5)=((8R)/5)(((2R)/5)+g) tan α=(v_y /v_x )=((4R)/5)+2g (for R=5 and g=10 α=87.61 tan α=24)

$$\boldsymbol{\mathrm{C}}\mathrm{alcul}\:\mathrm{de}\:\mathrm{tan}\:\boldsymbol{\alpha} \\ $$$$\mathrm{Mouvfment}\:\mathrm{de}\:\:\boldsymbol{\mathrm{A}}\rightarrow\boldsymbol{\mathrm{C}} \\ $$$$\:\:\mathrm{a}=\mathrm{g}=\mathrm{g}_{\mathrm{y}} =+\mathrm{g}\:\:\:\:\Rightarrow\:\mathrm{v}_{\mathrm{y}} =\mathrm{gt}+\mathrm{v}_{\mathrm{0}} \\ $$$$\:\:\mathrm{a}_{\mathrm{x}} =\mathrm{0}\:\:\:\:\:\:\Rightarrow\mathrm{v}_{\mathrm{x}} =\mathrm{cte}=\frac{\mathrm{4}}{\mathrm{5}}\mathrm{R}=\mathrm{Rcos}\:\theta \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:\:\begin{cases}{\mathrm{cos}\:\theta=\frac{\mathrm{4}}{\mathrm{5}}}\\{\mathrm{sin}\:\theta=\frac{\mathrm{3}}{\mathrm{5}}}\end{cases} \\ $$$$\:\:\mathrm{v}_{\mathrm{0}} =\begin{cases}{\mathrm{v}_{\mathrm{0x}} =\frac{\mathrm{4R}}{\mathrm{5}}}\\{\mathrm{v}_{\mathrm{0y}} =\frac{\mathrm{3R}}{\mathrm{5}}}\end{cases} \\ $$$$\:\:\:\mid\mid\mathrm{V}_{\mathrm{0}} \mid\mid=\sqrt{\mathrm{v}_{\mathrm{0x}} ^{\mathrm{2}} +\mathrm{v}_{\mathrm{0y}} ^{\mathrm{2}} }=\mathrm{R} \\ $$$$\:\:\:\:\mathrm{A}\left(\mathrm{0},\mathrm{0}\right)\:\:\:\mathrm{B}\left(\frac{\mathrm{4R}}{\mathrm{5}},\mathrm{0}\right)\:\:;\left(\:\mathrm{C}\left(\frac{\mathrm{4R}}{\mathrm{5}};\frac{\mathrm{8R}}{\mathrm{5}}\right)\right. \\ $$$$\:\:\begin{cases}{\mathrm{v}_{\mathrm{y}} =\mathrm{gt}+\frac{\mathrm{3R}}{\mathrm{5}}\:\:\:\:\:\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} +\frac{\mathrm{3R}}{\mathrm{5}}\mathrm{t}+\mathrm{y}_{\mathrm{0}} }\\{\mathrm{v}_{\mathrm{x}} =\frac{\mathrm{4R}}{\mathrm{5}}=\mathrm{v}_{\mathrm{0}\:\mathrm{x}} \:\:\:\:\mathrm{x}=\frac{\mathrm{4R}}{\mathrm{5}}\mathrm{t}}\end{cases} \\ $$$$\:\:\mathrm{au}\:\mathrm{point}\:\mathrm{C}\:\left(\mathrm{x}=\frac{\mathrm{4R}}{\mathrm{5}}\:\:;\:\:\:\mathrm{y}=\frac{\mathrm{8R}}{\mathrm{5}}\right)\:\: \\ $$$$\:\:\frac{\mathrm{8R}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} +\frac{\mathrm{3R}}{\mathrm{5}}\mathrm{t}\:\:\:\:\:\:\:\:\mathrm{x}=\:\frac{\mathrm{4R}}{\mathrm{5}}\mathrm{t} \\ $$$$\mathrm{v}^{\mathrm{2}} −\mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2g}\left(\mathrm{x}−\mathrm{x}_{\mathrm{0}} \right)=\mathrm{2gx} \\ $$$$\:\:\mid\mid\mathrm{v}^{\mathrm{2}} \mid\mid=\mathrm{v}_{\mathrm{x}} ^{\mathrm{2}} +\mathrm{v}_{\mathrm{y}} ^{\mathrm{2}} =\:\:\frac{\mathrm{16R}^{\mathrm{2}} }{\mathrm{25}}+\frac{\mathrm{8}\boldsymbol{\mathrm{g}}\mathrm{R}}{\mathrm{5}}=\frac{\mathrm{8R}}{\mathrm{5}}\left(\frac{\mathrm{2R}}{\mathrm{5}}+\mathrm{g}\right) \\ $$$$\:\:\:\mathrm{tan}\:\alpha=\frac{\mathrm{v}_{\mathrm{y}} }{\mathrm{v}_{\mathrm{x}} }=\frac{\mathrm{4R}}{\mathrm{5}}+\mathrm{2}\boldsymbol{\mathrm{g}} \\ $$$$\left({for}\:\:{R}=\mathrm{5}\:\:\mathrm{and}\:\:\mathrm{g}=\mathrm{10}\:\:\alpha=\mathrm{87}.\mathrm{61}\:\:\mathrm{tan}\:\alpha=\mathrm{24}\right) \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 01/Nov/24

Commented by mr W last updated on 01/Nov/24

very wrong! tan α has no unit. R has the unit of length [m]. g has the unit of acceleration [m/s^2 ]. tan α=((4R)/5)+2g makes never sense! just like we can not say the angle is equal to the sum from 4 meters and 2 kilograms.

$${very}\:{wrong}! \\ $$$$\mathrm{tan}\:\alpha\:{has}\:{no}\:{unit}. \\ $$$${R}\:{has}\:{the}\:{unit}\:{of}\:{length}\:\left[{m}\right]. \\ $$$${g}\:{has}\:{the}\:{unit}\:{of}\:{acceleration}\:\left[{m}/{s}^{\mathrm{2}} \right]. \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{4}{R}}{\mathrm{5}}+\mathrm{2}{g}\:{makes}\:{never}\:{sense}! \\ $$$${just}\:{like}\:{we}\:{can}\:{not}\:{say} \\ $$$${the}\:{angle}\:{is}\:{equal}\:{to}\:{the}\:{sum}\:{from}\: \\ $$$$\mathrm{4}\:{meters}\:{and}\:\mathrm{2}\:{kilograms}. \\ $$

Answered by mr W last updated on 01/Nov/24

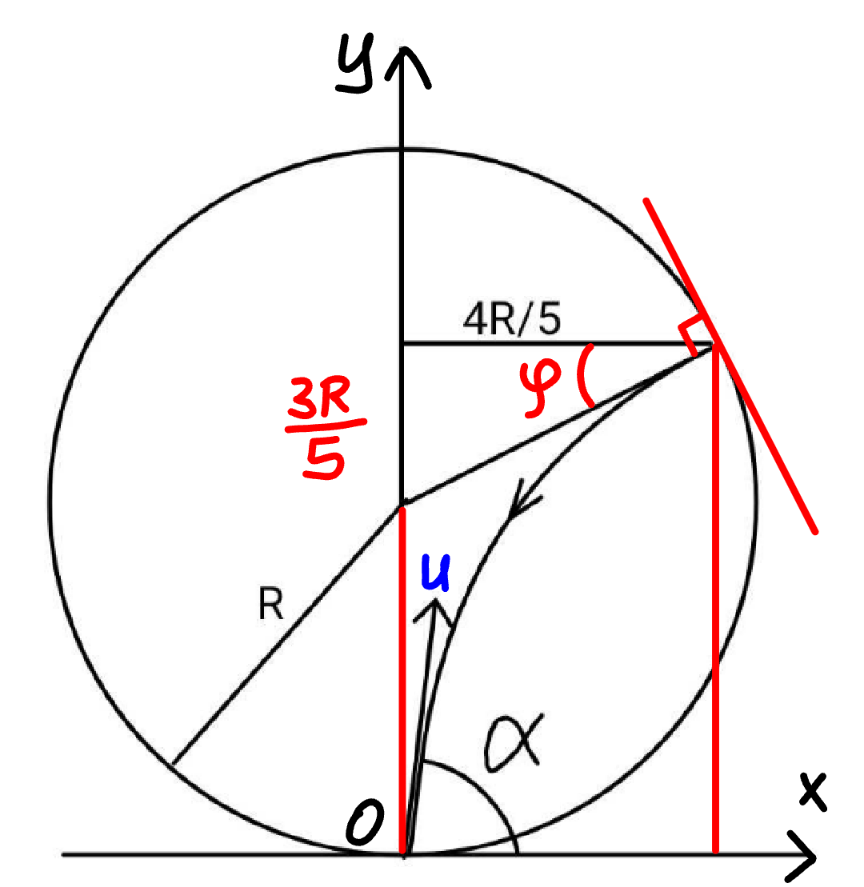
Commented by mr W last updated on 01/Nov/24

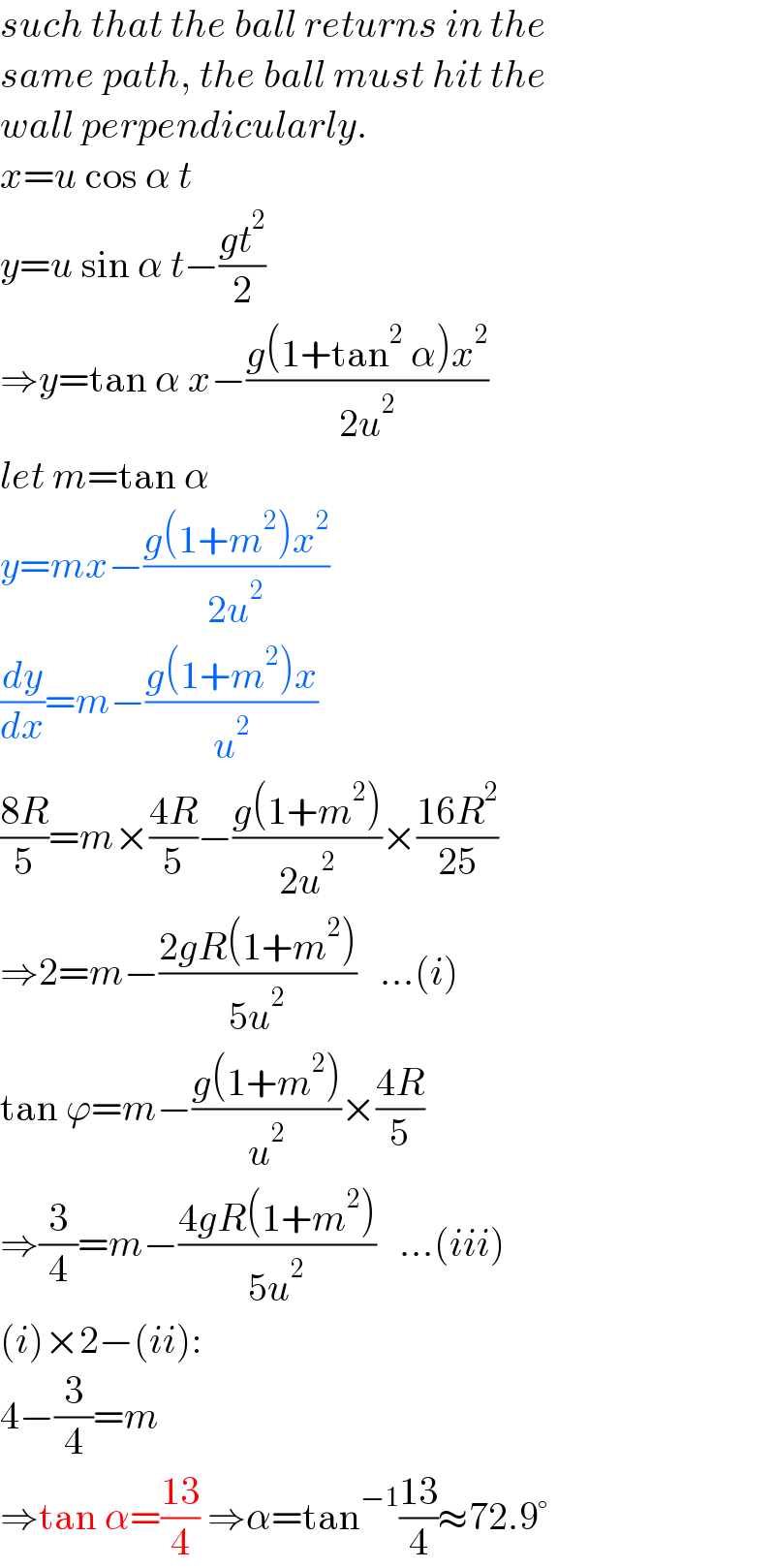
such that the ball returns in the same path, the ball must hit the wall perpendicularly. x=u cos α t y=u sin α t−((gt^2 )/2) ⇒y=tan α x−((g(1+tan^2 α)x^2 )/(2u^2 )) let m=tan α y=mx−((g(1+m^2 )x^2 )/(2u^2 )) (dy/dx)=m−((g(1+m^2 )x)/u^2 ) ((8R)/5)=m×((4R)/5)−((g(1+m^2 ))/(2u^2 ))×((16R^2 )/(25)) ⇒2=m−((2gR(1+m^2 ))/(5u^2 )) ...(i) tan ϕ=m−((g(1+m^2 ))/u^2 )×((4R)/5) ⇒(3/4)=m−((4gR(1+m^2 ))/(5u^2 )) ...(iii) (i)×2−(ii): 4−(3/4)=m ⇒tan α=((13)/4) ⇒α=tan^(−1) ((13)/4)≈72.9°

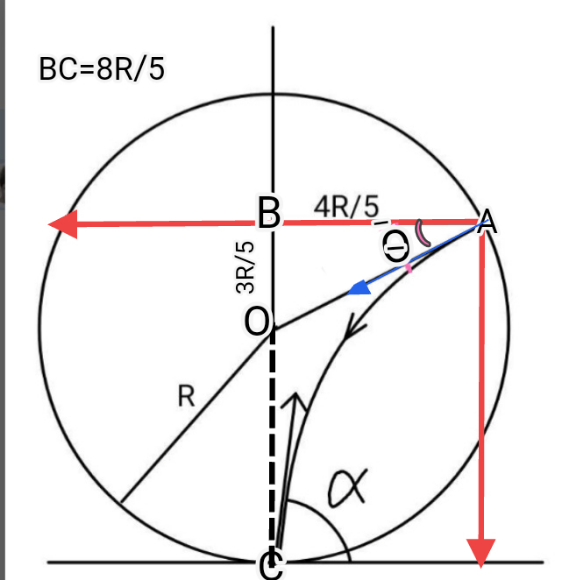
$${such}\:{that}\:{the}\:{ball}\:{returns}\:{in}\:{the} \\ $$$${same}\:{path},\:{the}\:{ball}\:{must}\:{hit}\:{the} \\ $$$${wall}\:{perpendicularly}. \\ $$$${x}={u}\:\mathrm{cos}\:\alpha\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\alpha\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{y}=\mathrm{tan}\:\alpha\:{x}−\frac{{g}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha\right){x}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${let}\:{m}=\mathrm{tan}\:\alpha \\ $$$${y}={mx}−\frac{{g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}={m}−\frac{{g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}}{{u}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{8}{R}}{\mathrm{5}}={m}×\frac{\mathrm{4}{R}}{\mathrm{5}}−\frac{{g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{2}{u}^{\mathrm{2}} }×\frac{\mathrm{16}{R}^{\mathrm{2}} }{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{2}={m}−\frac{\mathrm{2}{gR}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{5}{u}^{\mathrm{2}} }\:\:\:...\left({i}\right) \\ $$$$\mathrm{tan}\:\varphi={m}−\frac{{g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} }×\frac{\mathrm{4}{R}}{\mathrm{5}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{4}}={m}−\frac{\mathrm{4}{gR}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{5}{u}^{\mathrm{2}} }\:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)×\mathrm{2}−\left({ii}\right): \\ $$$$\mathrm{4}−\frac{\mathrm{3}}{\mathrm{4}}={m} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{13}}{\mathrm{4}}\:\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{13}}{\mathrm{4}}\approx\mathrm{72}.\mathrm{9}° \\ $$

Commented by a.lgnaoui last updated on 01/Nov/24

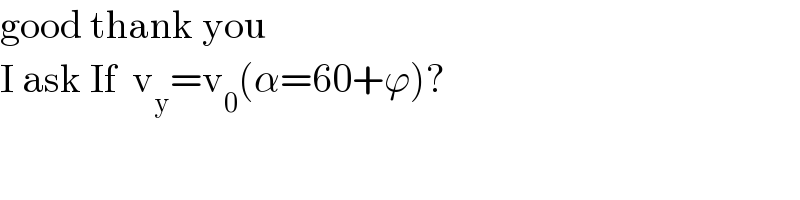
good thank you I ask If v_y =v_0 (α=60+ϕ)?

$$\mathrm{good}\:\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{I}\:\mathrm{ask}\:\mathrm{If}\:\:\mathrm{v}_{\mathrm{y}} =\mathrm{v}_{\mathrm{0}} \left(\alpha=\mathrm{60}+\varphi\right)? \\ $$

Commented by mr W last updated on 01/Nov/24

no.

$${no}. \\ $$

Commented by ajfour last updated on 01/Nov/24

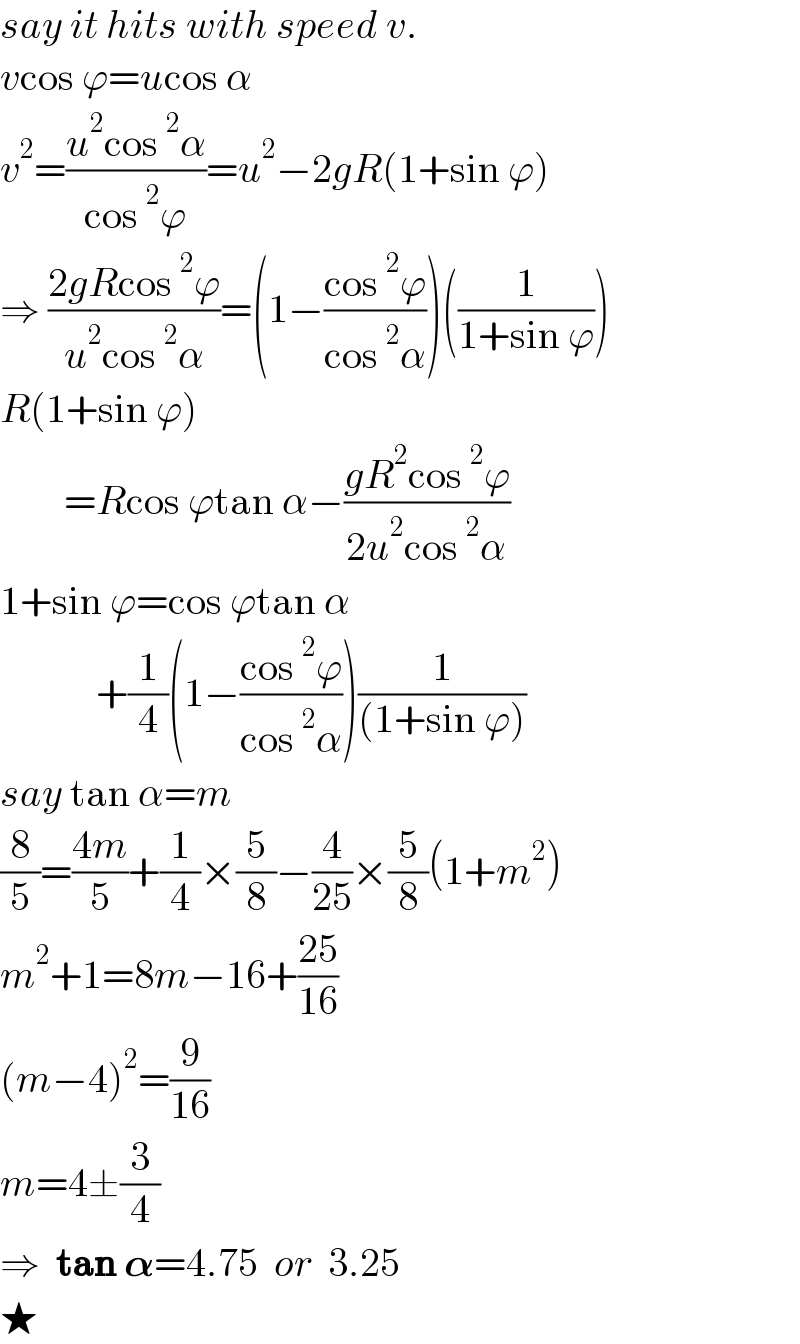
say it hits with speed v. vcos ϕ=ucos α v^2 =((u^2 cos^2 α)/(cos^2 ϕ))=u^2 −2gR(1+sin ϕ) ⇒ ((2gRcos^2 ϕ)/(u^2 cos^2 α))=(1−((cos^2 ϕ)/(cos^2 α)))((1/(1+sin ϕ))) R(1+sin ϕ) =Rcos ϕtan α−((gR^2 cos^2 ϕ)/(2u^2 cos^2 α)) 1+sin ϕ=cos ϕtan α +(1/4)(1−((cos^2 ϕ)/(cos^2 α)))(1/((1+sin ϕ))) say tan α=m (8/5)=((4m)/5)+(1/4)×(5/8)−(4/(25))×(5/8)(1+m^2 ) m^2 +1=8m−16+((25)/(16)) (m−4)^2 =(9/(16)) m=4±(3/4) ⇒ tan 𝛂=4.75 or 3.25 ★

$${say}\:{it}\:{hits}\:{with}\:{speed}\:{v}. \\ $$$${v}\mathrm{cos}\:\varphi={u}\mathrm{cos}\:\alpha \\ $$$${v}^{\mathrm{2}} =\frac{{u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha}{\mathrm{cos}\:^{\mathrm{2}} \varphi}={u}^{\mathrm{2}} −\mathrm{2}{gR}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right) \\ $$$$\Rightarrow\:\frac{\mathrm{2}{gR}\mathrm{cos}\:^{\mathrm{2}} \varphi}{{u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha}=\left(\mathrm{1}−\frac{\mathrm{cos}\:^{\mathrm{2}} \varphi}{\mathrm{cos}\:^{\mathrm{2}} \alpha}\right)\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\varphi}\right) \\ $$$${R}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right) \\ $$$$\:\:\:\:\:\:\:\:={R}\mathrm{cos}\:\varphi\mathrm{tan}\:\alpha−\frac{{gR}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \varphi}{\mathrm{2}{u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha} \\ $$$$\mathrm{1}+\mathrm{sin}\:\varphi=\mathrm{cos}\:\varphi\mathrm{tan}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}−\frac{\mathrm{cos}\:^{\mathrm{2}} \varphi}{\mathrm{cos}\:^{\mathrm{2}} \alpha}\right)\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)} \\ $$$${say}\:\mathrm{tan}\:\alpha={m} \\ $$$$\frac{\mathrm{8}}{\mathrm{5}}=\frac{\mathrm{4}{m}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{8}}−\frac{\mathrm{4}}{\mathrm{25}}×\frac{\mathrm{5}}{\mathrm{8}}\left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$${m}^{\mathrm{2}} +\mathrm{1}=\mathrm{8}{m}−\mathrm{16}+\frac{\mathrm{25}}{\mathrm{16}} \\ $$$$\left({m}−\mathrm{4}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{16}} \\ $$$${m}=\mathrm{4}\pm\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}=\mathrm{4}.\mathrm{75}\:\:{or}\:\:\mathrm{3}.\mathrm{25} \\ $$$$\bigstar \\ $$

Commented by ajfour last updated on 01/Nov/24

Thank you mrW sir, I got two answers, both i hope are correct; one is same as yours.

$${Thank}\:{you}\:{mrW}\:{sir},\:{I}\:{got}\:{two} \\ $$$${answers},\:{both}\:{i}\:{hope}\:{are}\:{correct}; \\ $$$${one}\:{is}\:{same}\:{as}\:{yours}. \\ $$

Commented by Ghisom last updated on 01/Nov/24

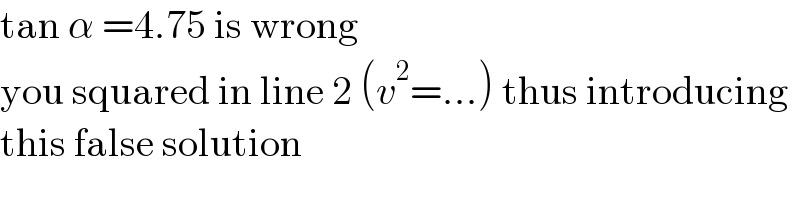
tan α =4.75 is wrong you squared in line 2 (v^2 =...) thus introducing this false solution

$$\mathrm{tan}\:\alpha\:=\mathrm{4}.\mathrm{75}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{you}\:\mathrm{squared}\:\mathrm{in}\:\mathrm{line}\:\mathrm{2}\:\left({v}^{\mathrm{2}} =...\right)\:\mathrm{thus}\:\mathrm{introducing} \\ $$$$\mathrm{this}\:\mathrm{false}\:\mathrm{solution} \\ $$

Commented by mr W last updated on 01/Nov/24

only with m=((13)/4) the ball returns back following the same path, the green path.

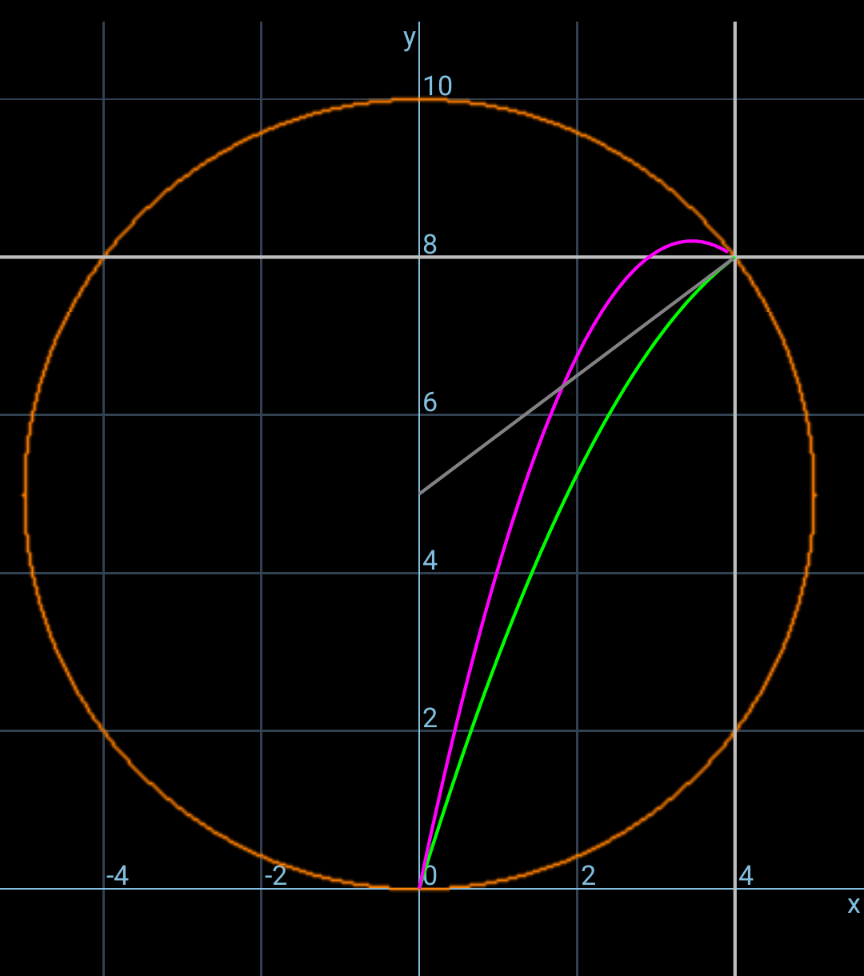
$${only}\:{with}\:{m}=\frac{\mathrm{13}}{\mathrm{4}}\:{the}\:{ball}\:{returns}\:{back} \\ $$$${following}\:{the}\:{same}\:{path},\:{the}\:{green}\: \\ $$$${path}. \\ $$

Commented by mr W last updated on 01/Nov/24

Commented by ajfour last updated on 02/Nov/24

yes, thank you; so it indeed seems.

$${yes},\:{thank}\:{you};\:{so}\:{it}\:{indeed}\:{seems}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com