Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 213201 by ajfour last updated on 01/Nov/24

Commented by ajfour last updated on 01/Nov/24

Find R

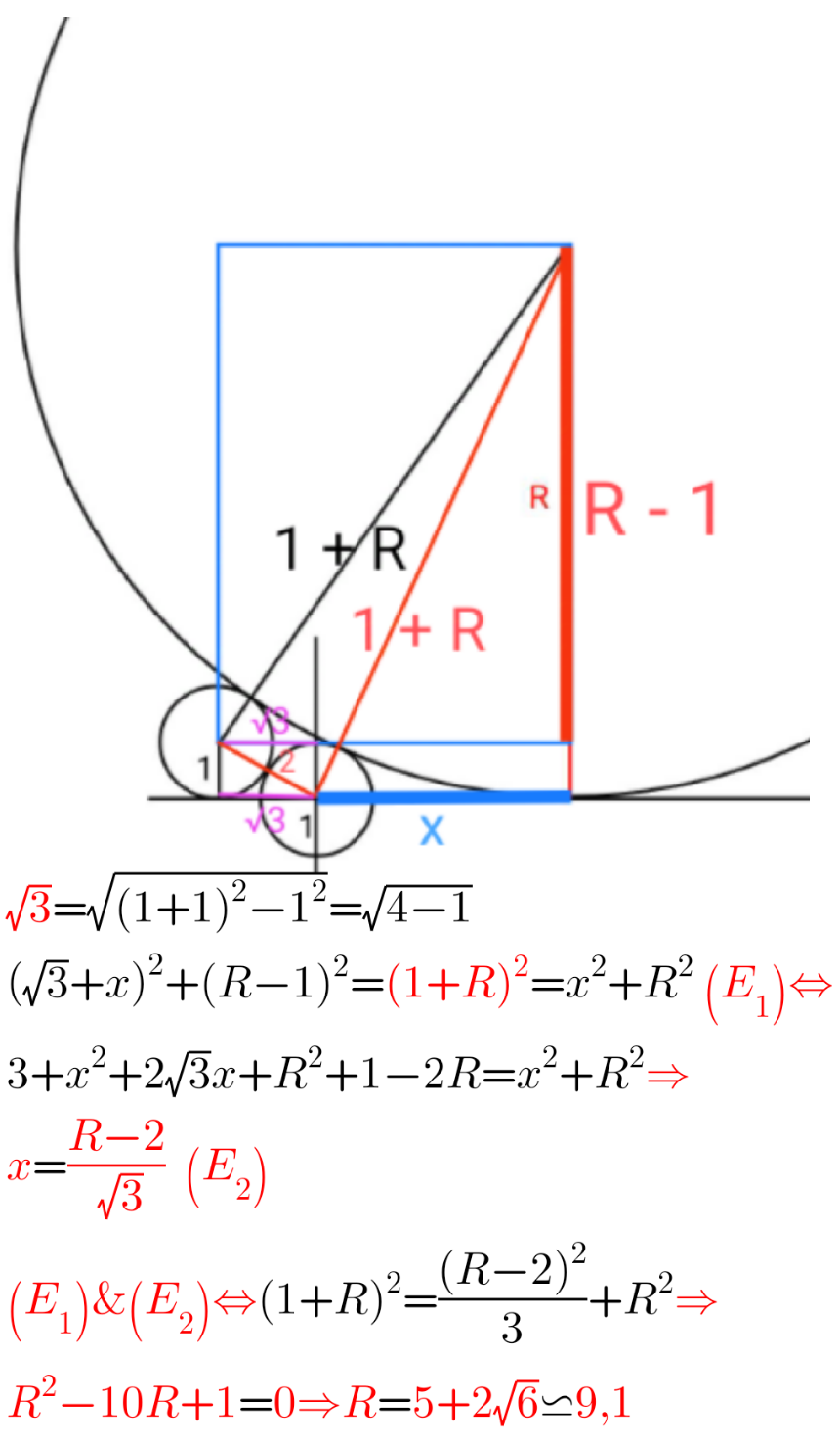
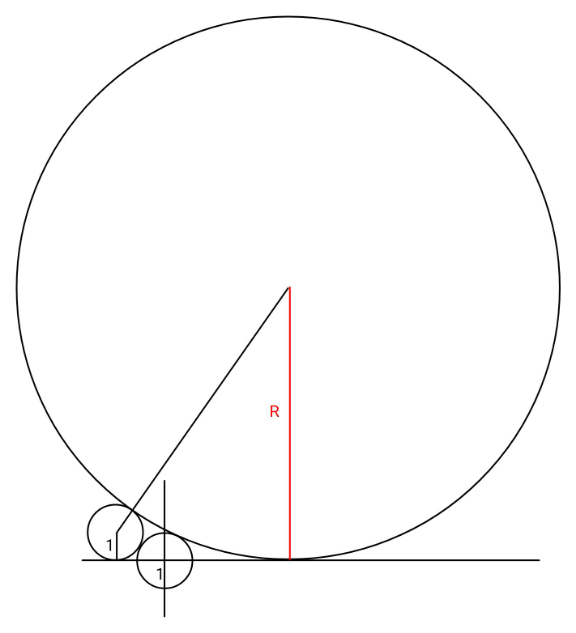
$${Find}\:{R} \\ $$

Answered by A5T last updated on 01/Nov/24

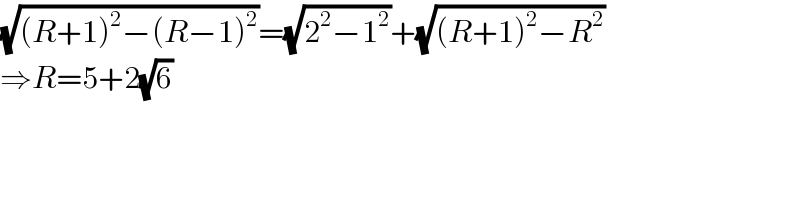
(√((R+1)^2 −(R−1)^2 ))=(√(2^2 −1^2 ))+(√((R+1)^2 −R^2 )) ⇒R=5+2(√6)

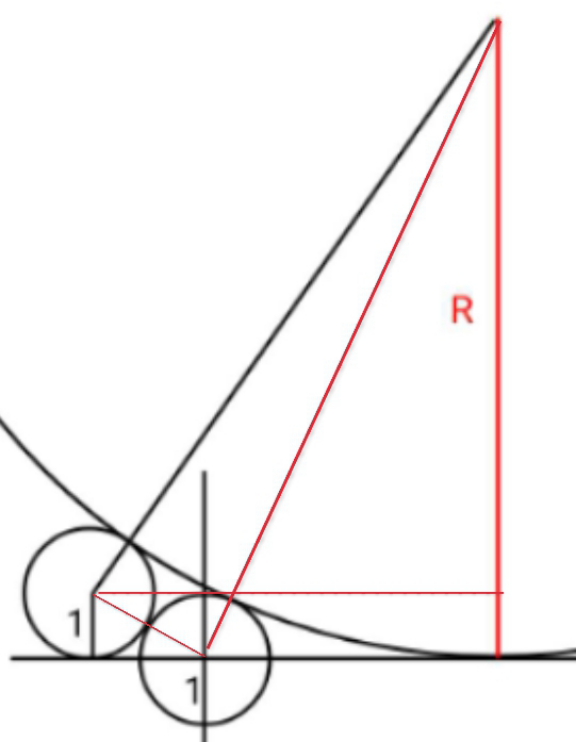
$$\sqrt{\left({R}+\mathrm{1}\right)^{\mathrm{2}} −\left({R}−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{2}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\sqrt{\left({R}+\mathrm{1}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} } \\ $$$$\Rightarrow{R}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$

Commented by A5T last updated on 01/Nov/24

Commented by ajfour last updated on 01/Nov/24

Wow, excellent.

$${Wow},\:{excellent}. \\ $$

Commented by ajfour last updated on 01/Nov/24

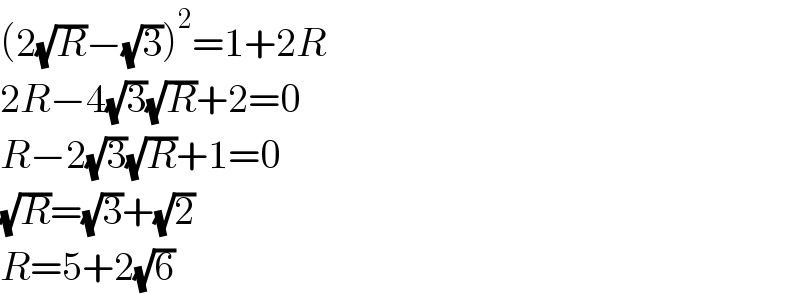
(2(√R)−(√3))^2 =1+2R 2R−4(√3)(√R)+2=0 R−2(√3)(√R)+1=0 (√R)=(√3)+(√2) R=5+2(√6)

$$\left(\mathrm{2}\sqrt{{R}}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{R} \\ $$$$\mathrm{2}{R}−\mathrm{4}\sqrt{\mathrm{3}}\sqrt{{R}}+\mathrm{2}=\mathrm{0} \\ $$$${R}−\mathrm{2}\sqrt{\mathrm{3}}\sqrt{{R}}+\mathrm{1}=\mathrm{0} \\ $$$$\sqrt{{R}}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}} \\ $$$${R}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$

Answered by cherokeesay last updated on 01/Nov/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com