
Question Number 212949 by Spillover last updated on 27/Oct/24
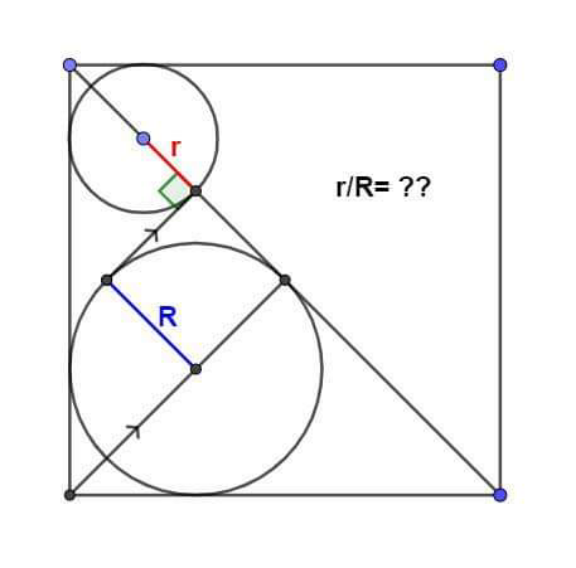
Answered by som(math1967) last updated on 27/Oct/24
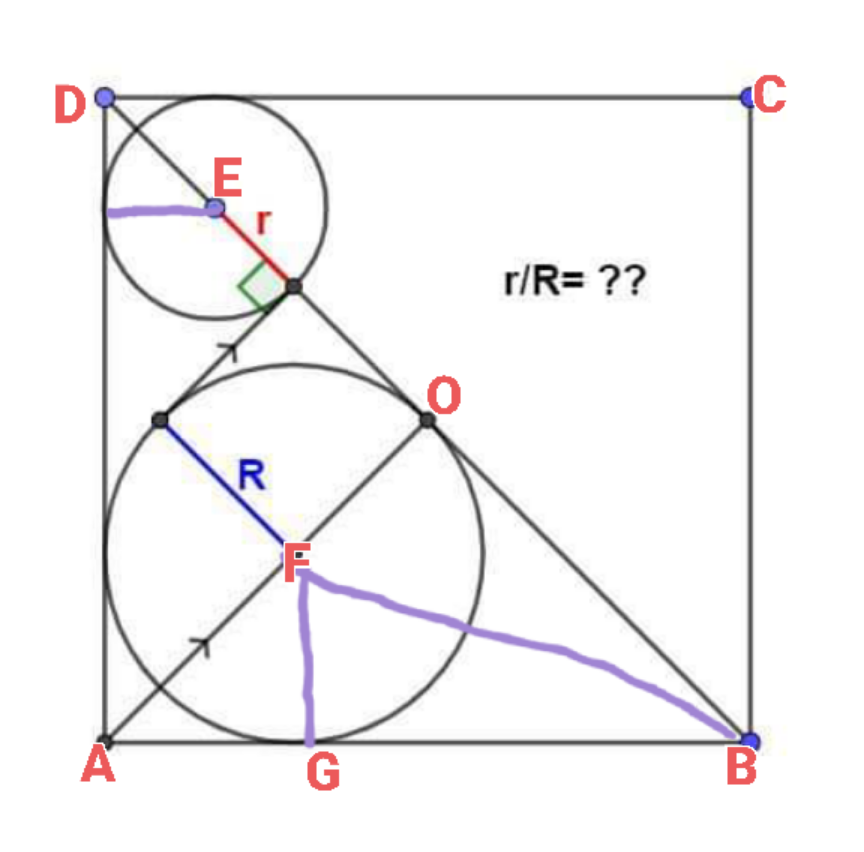
Commented by som(math1967) last updated on 27/Oct/24
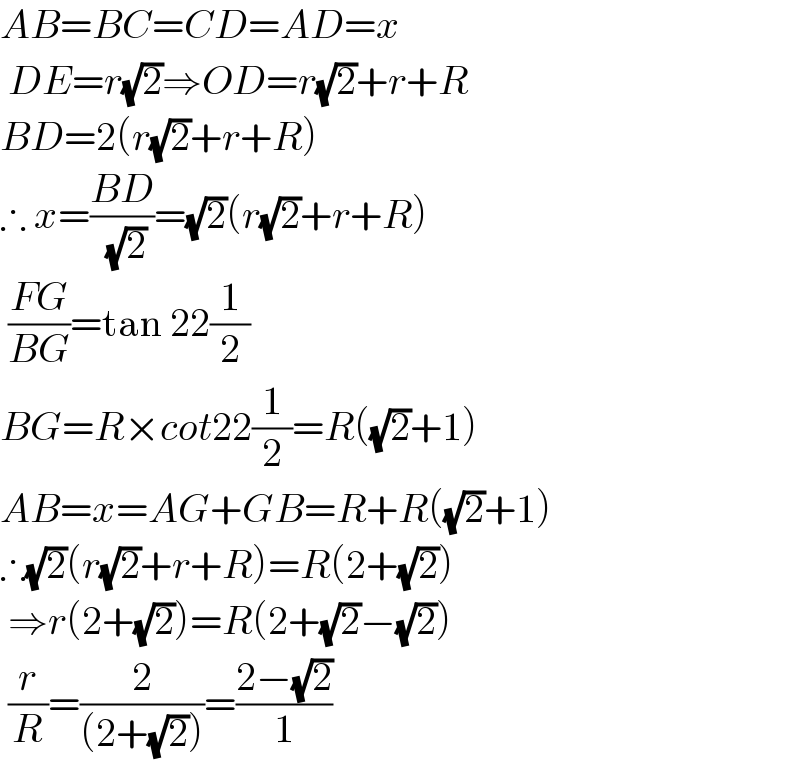
$${AB}={BC}={CD}={AD}={x} \\ $$$$\:{DE}={r}\sqrt{\mathrm{2}}\Rightarrow{OD}={r}\sqrt{\mathrm{2}}+{r}+{R} \\ $$$${BD}=\mathrm{2}\left({r}\sqrt{\mathrm{2}}+{r}+{R}\right) \\ $$$$\therefore\:{x}=\frac{{BD}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}\left({r}\sqrt{\mathrm{2}}+{r}+{R}\right) \\ $$$$\:\frac{{FG}}{{BG}}=\mathrm{tan}\:\mathrm{22}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${BG}={R}×{cot}\mathrm{22}\frac{\mathrm{1}}{\mathrm{2}}={R}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$${AB}={x}={AG}+{GB}={R}+{R}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\therefore\sqrt{\mathrm{2}}\left({r}\sqrt{\mathrm{2}}+{r}+{R}\right)={R}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right) \\ $$$$\:\Rightarrow{r}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)={R}\left(\mathrm{2}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}\right) \\ $$$$\:\frac{{r}}{{R}}=\frac{\mathrm{2}}{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{1}} \\ $$
Answered by ajfour last updated on 27/Oct/24
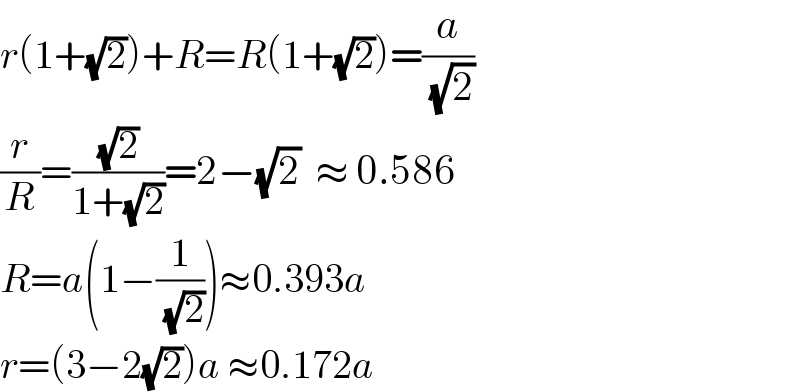
$${r}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+{R}={R}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{r}}{{R}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\mathrm{2}−\sqrt{\mathrm{2}}\:\:\approx\:\mathrm{0}.\mathrm{586} \\ $$$${R}={a}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\approx\mathrm{0}.\mathrm{393}{a}\:\:\: \\ $$$${r}=\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right){a}\:\approx\mathrm{0}.\mathrm{172}{a} \\ $$
Answered by A5T last updated on 27/Oct/24
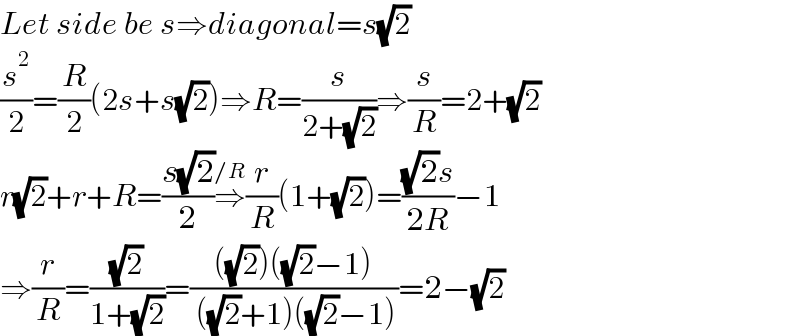
$${Let}\:{side}\:{be}\:{s}\Rightarrow{diagonal}={s}\sqrt{\mathrm{2}} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}=\frac{{R}}{\mathrm{2}}\left(\mathrm{2}{s}+{s}\sqrt{\mathrm{2}}\right)\Rightarrow{R}=\frac{{s}}{\mathrm{2}+\sqrt{\mathrm{2}}}\Rightarrow\frac{{s}}{{R}}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$${r}\sqrt{\mathrm{2}}+{r}+{R}=\frac{{s}\sqrt{\mathrm{2}}}{\mathrm{2}}\overset{/{R}} {\Rightarrow}\frac{{r}}{{R}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}}{s}}{\mathrm{2}{R}}−\mathrm{1} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\frac{\left(\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$
Answered by Spillover last updated on 27/Oct/24
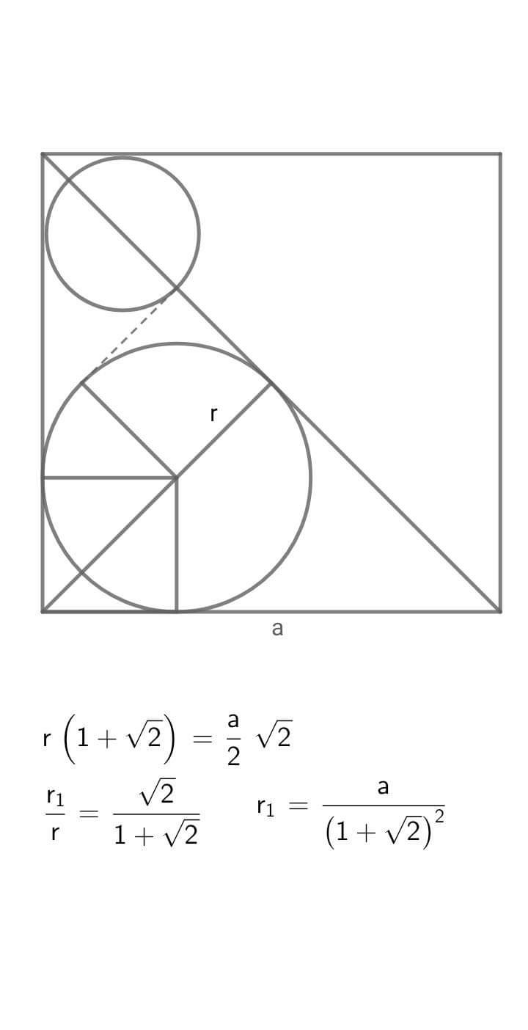
Answered by Spillover last updated on 27/Oct/24

$$ \\ $$R+√2R=R+r+√2r √2R=r+√2r r/R=√2/(1+√2) =√2(√2-1)/(2-1) =2-√2
