
Question Number 212901 by ajfour last updated on 26/Oct/24
Commented by ajfour last updated on 26/Oct/24

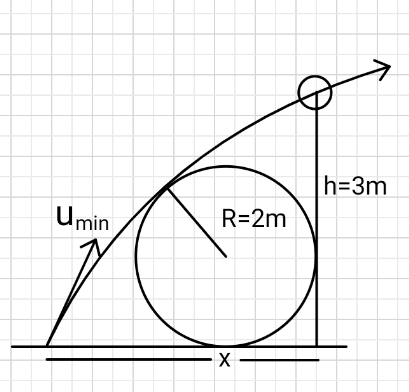
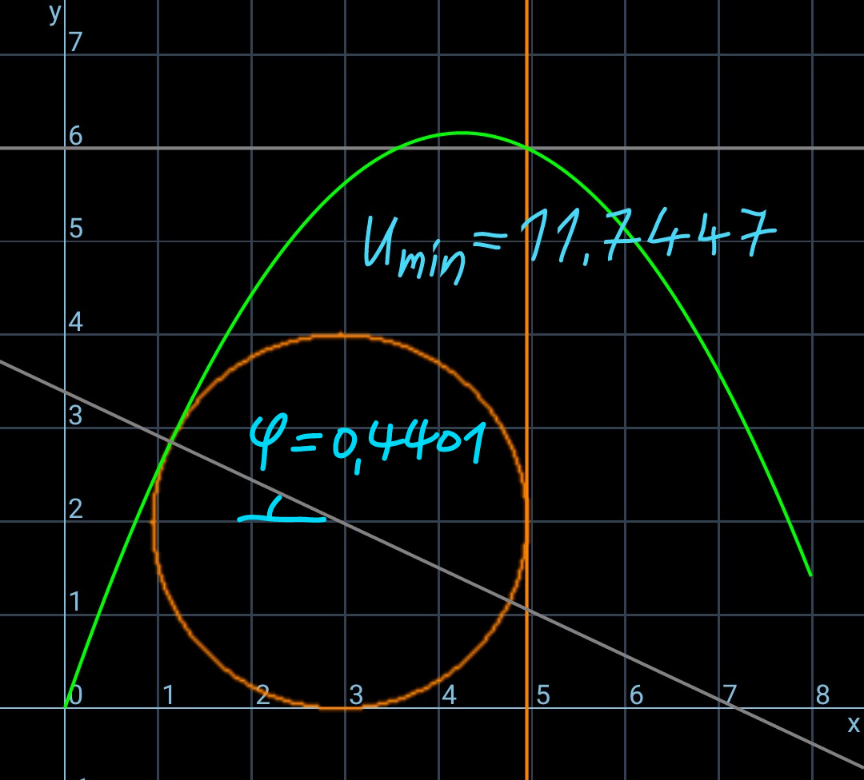
$${Find}\:{x}\:{and}\:{u}_{{min}} . \\ $$
Commented by ajfour last updated on 26/Oct/24
just published this on Magnetic Field (my video lecture on youtube) https://youtu.be/qx0TX9LSlzQ?si=S-eutbZgXcerKPSe
Answered by mr W last updated on 27/Oct/24
Commented by ajfour last updated on 27/Oct/24
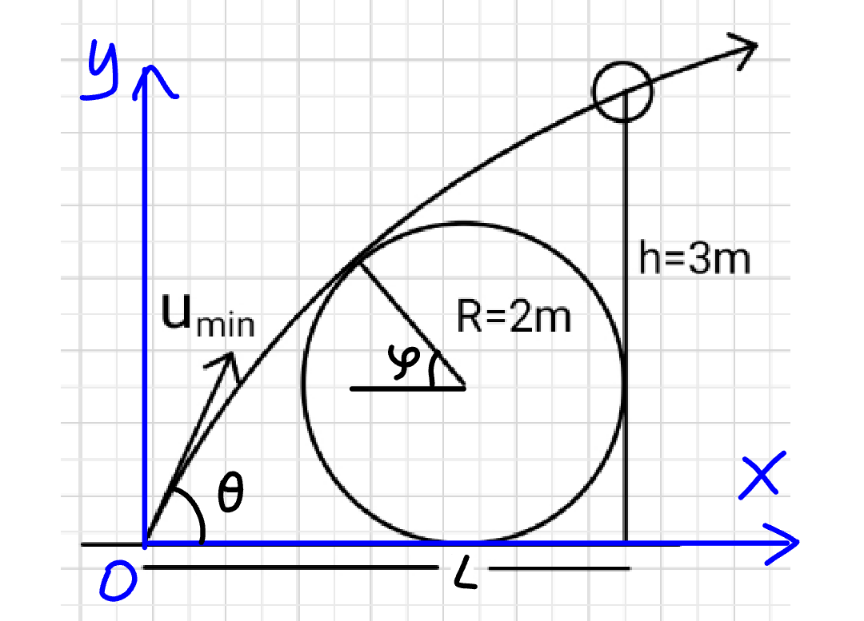
![let projectile launched from cylinder tangentially. h−R(1+sin ϕ)=R(1+cos ϕ)cot ϕ −((gR^2 (1+cos ϕ)^2 )/(2[u^2 −2gR(1+sin ϕ)]sin^2 ϕ)) For R=2, h=6 u=u_(min) when ϕ ≈ 0.4401 rad ≈ 25.2° from above applying differential calculus we find u_(min) for ϕ=ϕ_0 rewinding we see ball drops to ground when released tangentially from cylinder, so if v_0 =(√(u_(min) ^2 −2gR(1+sin ϕ_0 ))) Now L=R(1+cos ϕ_0 )+s −s=(v_0 sin ϕ)t −R(1+sin ϕ_0 )=(v_0 sin ϕ_0 )t−((gt^2 )/2) ★](Q212942.png)
$${let}\:{projectile}\:{launched}\:{from}\:{cylinder} \\ $$$${tangentially}. \\ $$$${h}−{R}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)={R}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)\mathrm{cot}\:\varphi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{gR}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\varphi\right)^{\mathrm{2}} }{\mathrm{2}\left[{u}^{\mathrm{2}} −\mathrm{2}{gR}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)\right]\underline{\mathrm{sin}\:^{\mathrm{2}} \varphi}} \\ $$$${For}\:{R}=\mathrm{2},\:{h}=\mathrm{6}\:\:\:\:{u}={u}_{{min}} \:\:{when} \\ $$$$\varphi\:\approx\:\mathrm{0}.\mathrm{4401}\:{rad}\:\approx\:\mathrm{25}.\mathrm{2}° \\ $$$${from}\:{above}\:{applying}\:{differential} \\ $$$${calculus}\:{we}\:{find}\:{u}_{{min}} \:{for}\:\varphi=\varphi_{\mathrm{0}} \\ $$$${rewinding}\:{we}\:{see}\:{ball}\:{drops}\:{to} \\ $$$${ground}\:{when}\:{released}\:{tangentially} \\ $$$${from}\:{cylinder},\:{so}\:{if} \\ $$$${v}_{\mathrm{0}} =\sqrt{{u}_{{min}} ^{\mathrm{2}} −\mathrm{2}{gR}\left(\mathrm{1}+\mathrm{sin}\:\varphi_{\mathrm{0}} \right)} \\ $$$${Now}\:{L}={R}\left(\mathrm{1}+\mathrm{cos}\:\varphi_{\mathrm{0}} \right)+{s} \\ $$$$−{s}=\left({v}_{\mathrm{0}} \mathrm{sin}\:\varphi\right){t} \\ $$$$−{R}\left(\mathrm{1}+\mathrm{sin}\:\varphi_{\mathrm{0}} \right)=\left({v}_{\mathrm{0}} \mathrm{sin}\:\varphi_{\mathrm{0}} \right){t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\bigstar \\ $$
Commented by mr W last updated on 27/Oct/24
![x=u cos θ t y=u sin θ t−((gt^2 )/2) y=tan θ x−(((1+tan^2 θ)gx^2 )/(2u^2 )) let m=tan θ y=mx−(((1+m^2 )gx^2 )/(2u^2 )) (dy/dx)=m−(((1+m^2 )gx)/u^2 ) at top of wall: h=mL−(((1+m^2 )gL^2 )/(2u^2 )) ⇒(h/R)=m((L/R))−(((1+m^2 )gR((L/R))^2 )/(2u^2 )) ...(i) at touching point on circle: x_P =L−R−R cos ϕ y_P =R(1+sin ϕ) R(1+sin ϕ)=m(L−R−R cos ϕ)−(((1+m^2 )g(L−R−R cos ϕ)^2 )/(2u^2 )) ⇒(1+sin ϕ)=m((L/R)−1−cos ϕ)−(((1+m^2 )gR((L/R)−1−cos ϕ)^2 )/(2u^2 )) ...(ii) (1/(tan ϕ))=m−(((1+m^2 )g(L−R−R cos ϕ))/u^2 ) ⇒(1/(tan ϕ))=m−(((1+m^2 )gR((L/R)−1−cos ϕ))/u^2 ) ...(iii) let ξ=(L/R), Φ=((gR)/(2u^2 )), μ=(h/R) μ=mξ−(1+m^2 )ξ^2 Φ ...(i) 1+sin ϕ=m(ξ−1−cos ϕ)−(1+m^2 )(ξ−1−cos ϕ)^2 Φ ...(ii) (1/(tan ϕ))=m−2(1+m^2 )(ξ−1−cos ϕ)Φ ...(iii) from (ii) and (iii): 2(1+sin ϕ)=(ξ−1−cos ϕ)(m+(1/(tan ϕ))) ⇒m=((2(1+sin ϕ))/(ξ−1−cos ϕ))−(1/(tan ϕ)) ...(iv) from (i) and (iii): (ξ^2 /(tan ϕ))=mξ^2 −2(ξ−1−cos ϕ)(mξ−μ) ...(v) (iv) into (v): ((1+sin ϕ)/(ξ−1−cos ϕ))−(1/(tan ϕ))−(1−((1+cos ϕ)/ξ))[((2(1+sin ϕ))/(ξ−1−cos ϕ))−(1/(tan ϕ))−(μ/ξ)]=0 ...(II) 2(1+sin ϕ)ξ^3 −[(1+sin ϕ)(3+2 cos ϕ)−(((1+cos ϕ−μ tan ϕ))/(tan ϕ))]ξ^2 −(((1+cos ϕ−2μ tan ϕ)(1+cos ϕ))/(tan ϕ))ξ−μ(1+cos ϕ)^2 =0 ...(II′) it′s clear that ξ>2. (iv) into (i): Φ=(([((2(1+sin ϕ))/(ξ−1−cos ϕ))−(1/(tan ϕ))]ξ−μ)/({1+[((2(1+sin ϕ))/(ξ−1−cos ϕ))−(1/(tan ϕ))]^2 }ξ^2 )) ...(I) now it is to find the maximum of Φ(ξ, ϕ), which means the minimum of u, under the condition (II).](Q212939.png)
$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}=\mathrm{tan}\:\theta\:{x}−\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right){gx}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${let}\:{m}=\mathrm{tan}\:\theta \\ $$$${y}={mx}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gx}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}={m}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gx}}{{u}^{\mathrm{2}} } \\ $$$$ \\ $$$${at}\:{top}\:{of}\:{wall}: \\ $$$${h}={mL}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gL}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{h}}{{R}}={m}\left(\frac{{L}}{{R}}\right)−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gR}\left(\frac{{L}}{{R}}\right)^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }\:\:\:\:...\left({i}\right) \\ $$$${at}\:{touching}\:{point}\:{on}\:{circle}: \\ $$$${x}_{{P}} ={L}−{R}−{R}\:\mathrm{cos}\:\varphi \\ $$$${y}_{{P}} ={R}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right) \\ $$$${R}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)={m}\left({L}−{R}−{R}\:\mathrm{cos}\:\varphi\right)−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){g}\left({L}−{R}−{R}\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)={m}\left(\frac{{L}}{{R}}−\mathrm{1}−\mathrm{cos}\:\varphi\right)−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gR}\left(\frac{{L}}{{R}}−\mathrm{1}−\mathrm{cos}\:\varphi\right)^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }\:\:\:\:...\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}={m}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){g}\left({L}−{R}−{R}\:\mathrm{cos}\:\varphi\right)}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}={m}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){gR}\left(\frac{{L}}{{R}}−\mathrm{1}−\mathrm{cos}\:\varphi\right)}{{u}^{\mathrm{2}} }\:\:\:...\left({iii}\right) \\ $$$${let}\:\xi=\frac{{L}}{{R}},\:\Phi=\frac{{gR}}{\mathrm{2}{u}^{\mathrm{2}} },\:\mu=\frac{{h}}{{R}} \\ $$$$\mu={m}\xi−\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\xi^{\mathrm{2}} \Phi\:\:\:\:...\left({i}\right) \\ $$$$\mathrm{1}+\mathrm{sin}\:\varphi={m}\left(\xi−\mathrm{1}−\mathrm{cos}\:\varphi\right)−\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\xi−\mathrm{1}−\mathrm{cos}\:\varphi\right)^{\mathrm{2}} \Phi\:\:\:\:...\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}={m}−\mathrm{2}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\xi−\mathrm{1}−\mathrm{cos}\:\varphi\right)\Phi\:\:\:...\left({iii}\right) \\ $$$${from}\:\left({ii}\right)\:{and}\:\left({iii}\right): \\ $$$$\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)=\left(\xi−\mathrm{1}−\mathrm{cos}\:\varphi\right)\left({m}+\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}\right) \\ $$$$\Rightarrow{m}=\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)}{\xi−\mathrm{1}−\mathrm{cos}\:\varphi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}\:\:\:\:...\left({iv}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({iii}\right): \\ $$$$\frac{\xi^{\mathrm{2}} }{\mathrm{tan}\:\varphi}={m}\xi^{\mathrm{2}} −\mathrm{2}\left(\xi−\mathrm{1}−\mathrm{cos}\:\varphi\right)\left({m}\xi−\mu\right)\:\:\:...\left({v}\right) \\ $$$$\left({iv}\right)\:{into}\:\left({v}\right): \\ $$$$\frac{\mathrm{1}+\mathrm{sin}\:\varphi}{\xi−\mathrm{1}−\mathrm{cos}\:\varphi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}−\left(\mathrm{1}−\frac{\mathrm{1}+\mathrm{cos}\:\varphi}{\xi}\right)\left[\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)}{\xi−\mathrm{1}−\mathrm{cos}\:\varphi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}−\frac{\mu}{\xi}\right]=\mathrm{0}\:\:\:...\left({II}\right) \\ $$$$\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)\xi^{\mathrm{3}} −\left[\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)\left(\mathrm{3}+\mathrm{2}\:\mathrm{cos}\:\varphi\right)−\frac{\left(\mathrm{1}+\mathrm{cos}\:\varphi−\mu\:\mathrm{tan}\:\varphi\right)}{\mathrm{tan}\:\varphi}\right]\xi^{\mathrm{2}} −\frac{\left(\mathrm{1}+\mathrm{cos}\:\varphi−\mathrm{2}\mu\:\mathrm{tan}\:\varphi\right)\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}{\mathrm{tan}\:\varphi}\xi−\mu\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)^{\mathrm{2}} =\mathrm{0}\:\:\:...\left({II}'\right) \\ $$$${it}'{s}\:{clear}\:{that}\:\xi>\mathrm{2}. \\ $$$$\left({iv}\right)\:{into}\:\left({i}\right): \\ $$$$\Phi=\frac{\left[\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)}{\xi−\mathrm{1}−\mathrm{cos}\:\varphi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}\right]\xi−\mu}{\left\{\mathrm{1}+\left[\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)}{\xi−\mathrm{1}−\mathrm{cos}\:\varphi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}\right]^{\mathrm{2}} \right\}\xi^{\mathrm{2}} }\:\:\:\:...\left({I}\right) \\ $$$${now}\:{it}\:{is}\:{to}\:{find}\:{the}\:{maximum}\:{of} \\ $$$$\Phi\left(\xi,\:\varphi\right),\:{which}\:{means}\:{the}\:{minimum} \\ $$$${of}\:{u},\:{under}\:{the}\:{condition}\:\left({II}\right). \\ $$
Commented by mr W last updated on 27/Oct/24
Commented by mr W last updated on 27/Oct/24
Commented by mr W last updated on 27/Oct/24
Commented by mr W last updated on 27/Oct/24
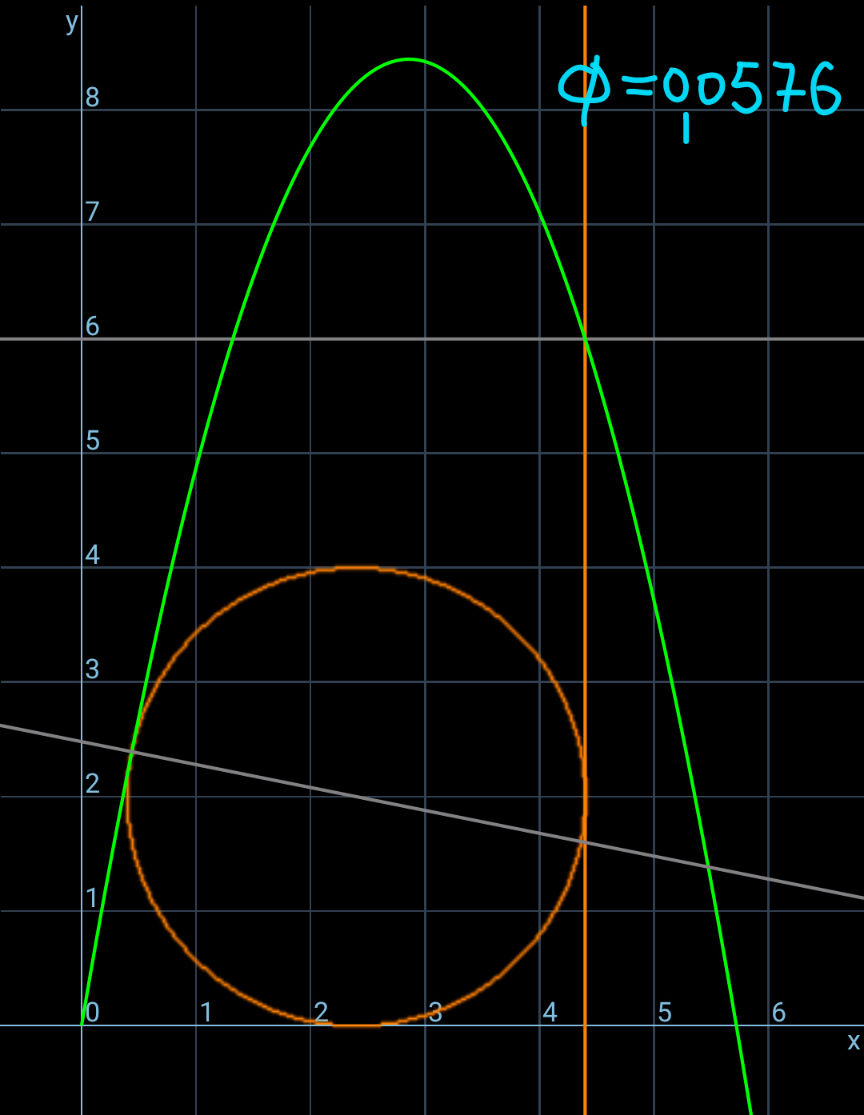
Commented by ajfour last updated on 27/Oct/24
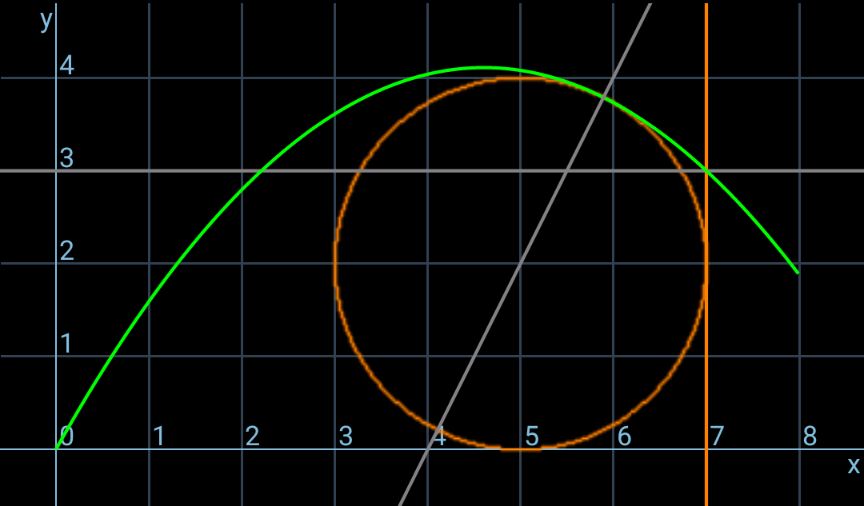
Commented by ajfour last updated on 27/Oct/24
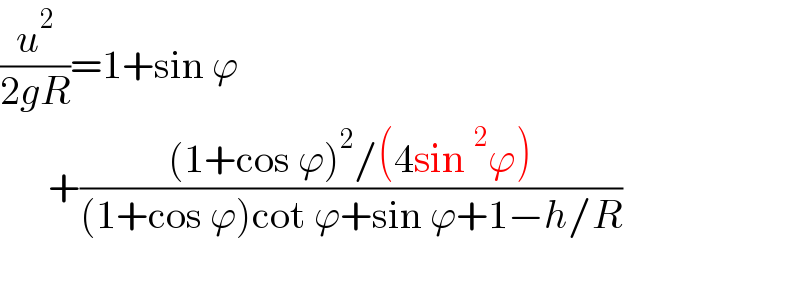
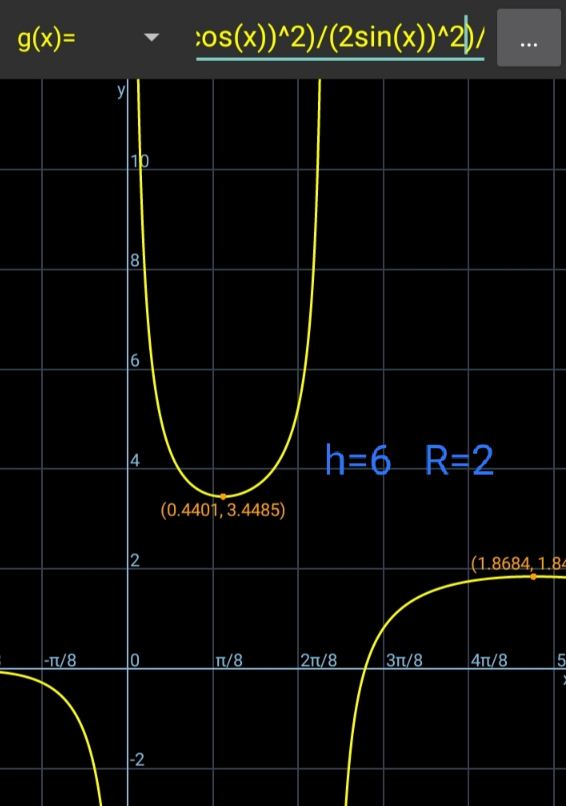
$$\frac{{u}^{\mathrm{2}} }{\mathrm{2}{gR}}=\mathrm{1}+\mathrm{sin}\:\varphi \\ $$$$\:\:\:\:\:\:+\frac{\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)^{\mathrm{2}} /\left(\mathrm{4sin}\:^{\mathrm{2}} \varphi\right)}{\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)\mathrm{cot}\:\varphi+\mathrm{sin}\:\varphi+\mathrm{1}−{h}/{R}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by mr W last updated on 27/Oct/24

$${yes},\:{that}'{s}\:{right}!\: \\ $$$${great}\:{approach}! \\ $$
Commented by mr W last updated on 27/Oct/24
Commented by ajfour last updated on 27/Oct/24
Thank you in everyrespect, sir.
