Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 212630 by efronzo1 last updated on 19/Oct/24

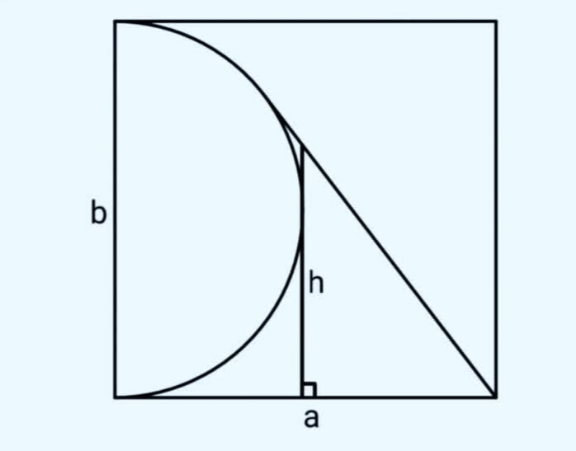
Commented by efronzo1 last updated on 19/Oct/24

$$\:\: \\ $$

Answered by mr W last updated on 19/Oct/24

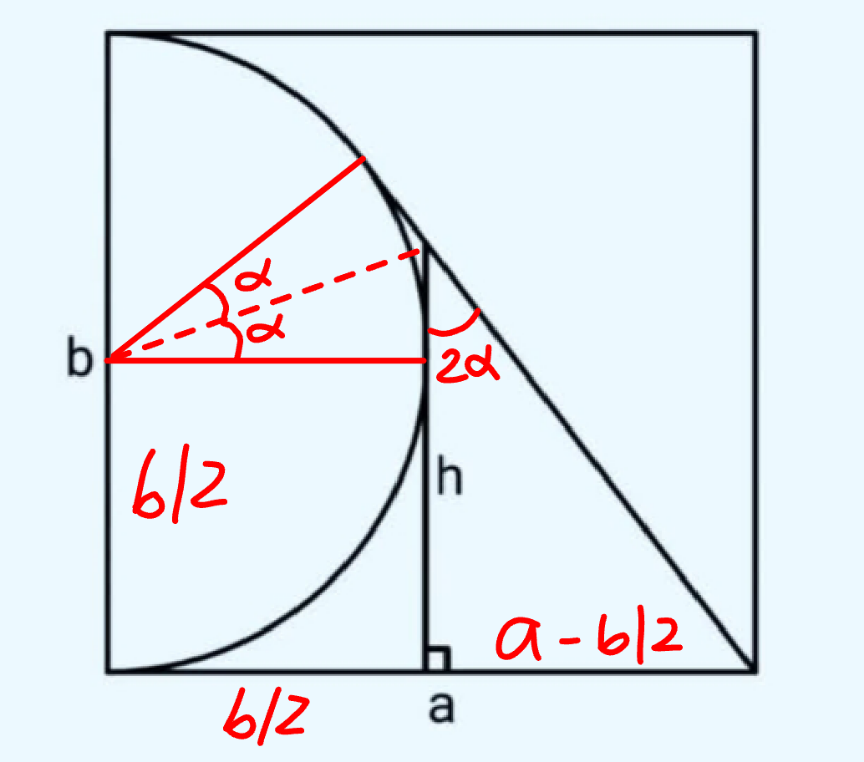
Commented by mr W last updated on 19/Oct/24

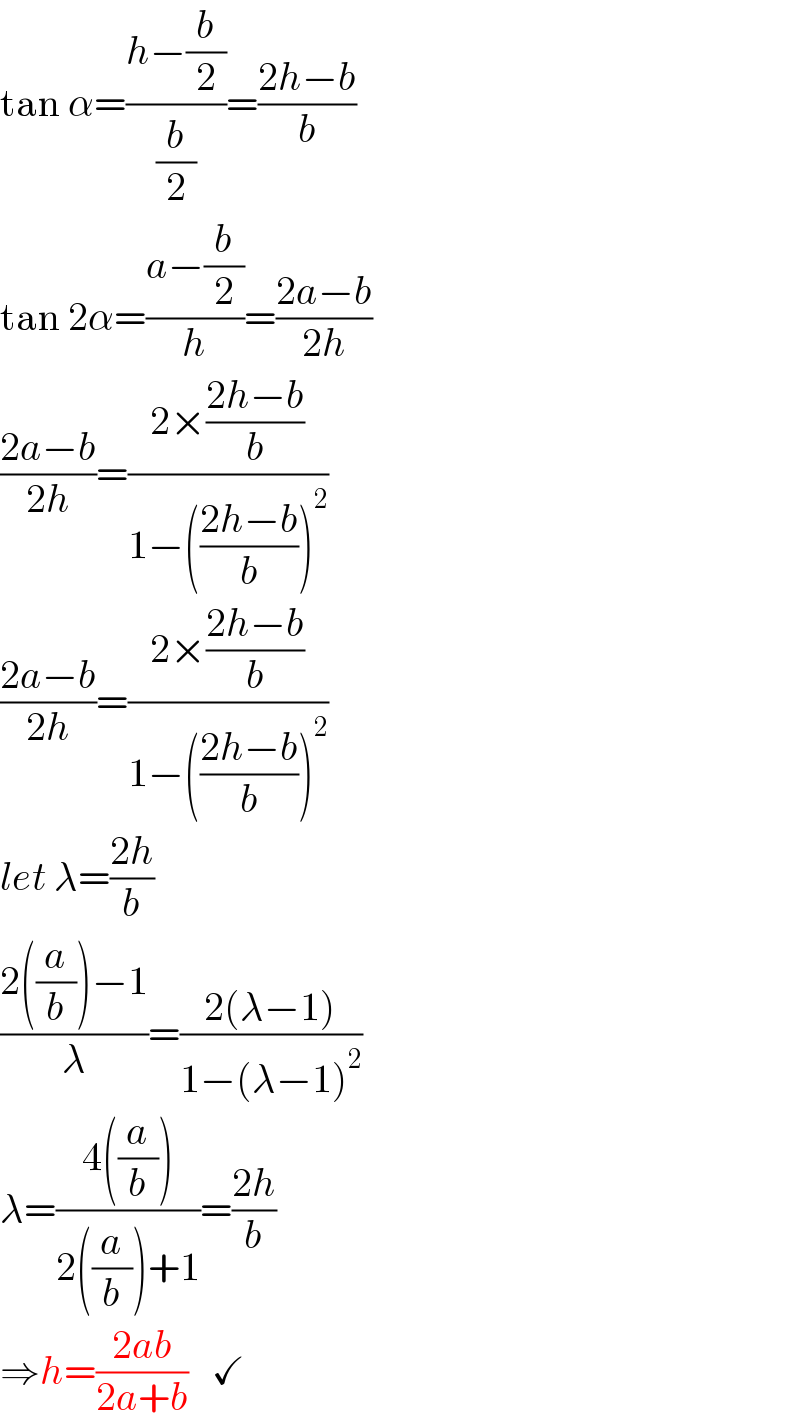
tan α=((h−(b/2))/(b/2))=((2h−b)/b) tan 2α=((a−(b/2))/h)=((2a−b)/(2h)) ((2a−b)/(2h))=((2×((2h−b)/b))/(1−(((2h−b)/b))^2 )) ((2a−b)/(2h))=((2×((2h−b)/b))/(1−(((2h−b)/b))^2 )) let λ=((2h)/b) ((2((a/b))−1)/λ)=((2(λ−1))/(1−(λ−1)^2 )) λ=((4((a/b)))/(2((a/b))+1))=((2h)/b) ⇒h=((2ab)/(2a+b)) ✓

$$\mathrm{tan}\:\alpha=\frac{{h}−\frac{{b}}{\mathrm{2}}}{\frac{{b}}{\mathrm{2}}}=\frac{\mathrm{2}{h}−{b}}{{b}} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{{a}−\frac{{b}}{\mathrm{2}}}{{h}}=\frac{\mathrm{2}{a}−{b}}{\mathrm{2}{h}} \\ $$$$\frac{\mathrm{2}{a}−{b}}{\mathrm{2}{h}}=\frac{\mathrm{2}×\frac{\mathrm{2}{h}−{b}}{{b}}}{\mathrm{1}−\left(\frac{\mathrm{2}{h}−{b}}{{b}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}{a}−{b}}{\mathrm{2}{h}}=\frac{\mathrm{2}×\frac{\mathrm{2}{h}−{b}}{{b}}}{\mathrm{1}−\left(\frac{\mathrm{2}{h}−{b}}{{b}}\right)^{\mathrm{2}} } \\ $$$${let}\:\lambda=\frac{\mathrm{2}{h}}{{b}} \\ $$$$\frac{\mathrm{2}\left(\frac{{a}}{{b}}\right)−\mathrm{1}}{\lambda}=\frac{\mathrm{2}\left(\lambda−\mathrm{1}\right)}{\mathrm{1}−\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\lambda=\frac{\mathrm{4}\left(\frac{{a}}{{b}}\right)}{\mathrm{2}\left(\frac{{a}}{{b}}\right)+\mathrm{1}}=\frac{\mathrm{2}{h}}{{b}} \\ $$$$\Rightarrow{h}=\frac{\mathrm{2}{ab}}{\mathrm{2}{a}+{b}}\:\:\:\checkmark \\ $$

Commented by Spillover last updated on 20/Oct/24

great

$${great} \\ $$

Answered by Spillover last updated on 19/Oct/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com