Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 212445 by ChantalYah last updated on 13/Oct/24

Commented by Frix last updated on 13/Oct/24

80cos A ? 150sin A =13 80cos A −150sin A =13 −170sin (A−tan^(−1) (8/(15))) =13 sin (A−tan^(−1) (8/(15))) =−((13)/(170)) A= { ((2nπ+tan^(−1) (8/(15)) −sin^(−1) ((13)/(170)))),(((2n+1)π+tan^(−1) (8/(15)) +sin^(−1) ((13)/(170)))) :} 80cos A +150sin A =13 170sin (A+tan^(−1) (8/(15))) =13 sin (A+tan^(−1) (8/(15))) =((13)/(170)) A= { ((2nπ−tan^(−1) (8/(15)) +sin^(−1) ((13)/(170)))),(((2n+1)π−tan^(−1) (8/(15)) −sin^(−1) ((13)/(170)))) :}

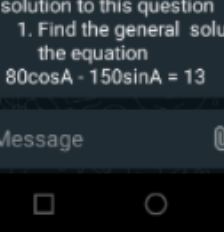
$$\mathrm{80cos}\:{A}\:?\:\mathrm{150sin}\:{A}\:=\mathrm{13} \\ $$$$ \\ $$$$\mathrm{80cos}\:{A}\:−\mathrm{150sin}\:{A}\:=\mathrm{13} \\ $$$$−\mathrm{170sin}\:\left({A}−\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\right)\:=\mathrm{13} \\ $$$$\mathrm{sin}\:\left({A}−\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\right)\:=−\frac{\mathrm{13}}{\mathrm{170}} \\ $$$${A}=\begin{cases}{\mathrm{2}{n}\pi+\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\:−\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{13}}{\mathrm{170}}}\\{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi+\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\:+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{13}}{\mathrm{170}}}\end{cases} \\ $$$$ \\ $$$$\mathrm{80cos}\:{A}\:+\mathrm{150sin}\:{A}\:=\mathrm{13} \\ $$$$\mathrm{170sin}\:\left({A}+\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\right)\:=\mathrm{13} \\ $$$$\mathrm{sin}\:\left({A}+\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\right)\:=\frac{\mathrm{13}}{\mathrm{170}} \\ $$$${A}=\begin{cases}{\mathrm{2}{n}\pi−\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\:+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{13}}{\mathrm{170}}}\\{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{8}}{\mathrm{15}}\:−\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{13}}{\mathrm{170}}}\end{cases} \\ $$

Answered by mr W last updated on 13/Oct/24

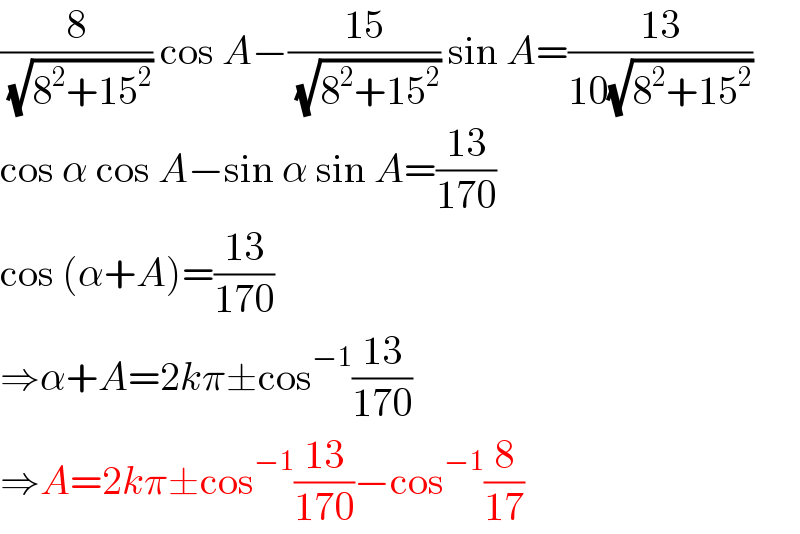
(8/( (√(8^2 +15^2 )))) cos A−((15)/( (√(8^2 +15^2 )))) sin A=((13)/(10(√(8^2 +15^2 )))) cos α cos A−sin α sin A=((13)/(170)) cos (α+A)=((13)/(170)) ⇒α+A=2kπ±cos^(−1) ((13)/(170)) ⇒A=2kπ±cos^(−1) ((13)/(170))−cos^(−1) (8/(17))

$$\frac{\mathrm{8}}{\:\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} }}\:\mathrm{cos}\:{A}−\frac{\mathrm{15}}{\:\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} }}\:\mathrm{sin}\:{A}=\frac{\mathrm{13}}{\mathrm{10}\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:{A}−\mathrm{sin}\:\alpha\:\mathrm{sin}\:{A}=\frac{\mathrm{13}}{\mathrm{170}} \\ $$$$\mathrm{cos}\:\left(\alpha+{A}\right)=\frac{\mathrm{13}}{\mathrm{170}} \\ $$$$\Rightarrow\alpha+{A}=\mathrm{2}{k}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{13}}{\mathrm{170}} \\ $$$$\Rightarrow{A}=\mathrm{2}{k}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{13}}{\mathrm{170}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{8}}{\mathrm{17}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com