
Question Number 212428 by Spillover last updated on 13/Oct/24
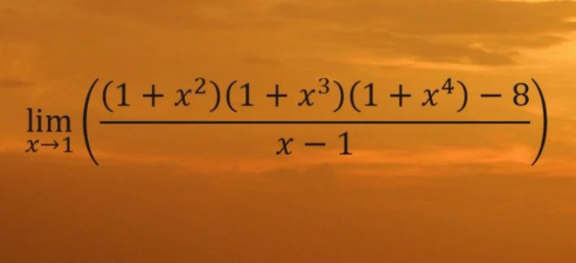
Answered by Yassine84 last updated on 13/Oct/24
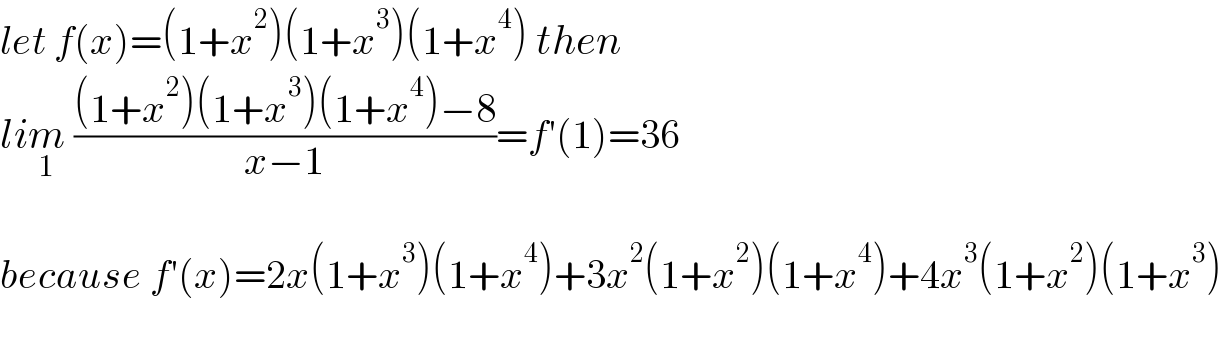
$${let}\:{f}\left({x}\right)=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\:{then} \\ $$$${li}\underset{\mathrm{1}} {{m}}\:\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)−\mathrm{8}}{{x}−\mathrm{1}}={f}'\left(\mathrm{1}\right)=\mathrm{36} \\ $$$$ \\ $$$${because}\:{f}'\left({x}\right)=\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)+\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)+\mathrm{4}{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right) \\ $$$$ \\ $$
Answered by golsendro last updated on 13/Oct/24
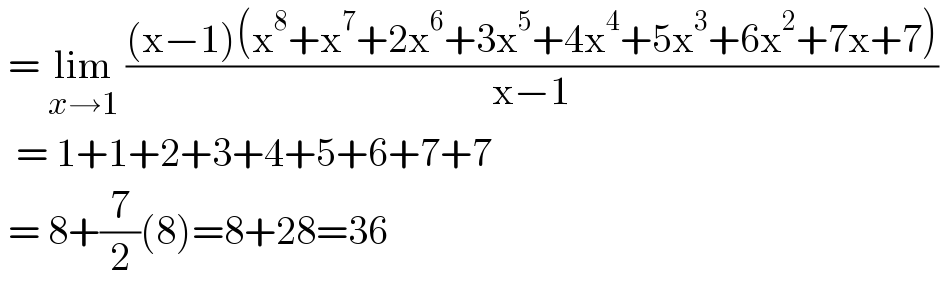
$$\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{8}} +\mathrm{x}^{\mathrm{7}} +\mathrm{2x}^{\mathrm{6}} +\mathrm{3x}^{\mathrm{5}} +\mathrm{4x}^{\mathrm{4}} +\mathrm{5x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{7}\right)}{\mathrm{x}−\mathrm{1}}\: \\ $$$$\:\:=\:\mathrm{1}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{7} \\ $$$$\:=\:\mathrm{8}+\frac{\mathrm{7}}{\mathrm{2}}\left(\mathrm{8}\right)=\mathrm{8}+\mathrm{28}=\mathrm{36} \\ $$
Answered by Nadirhashim last updated on 13/Oct/24
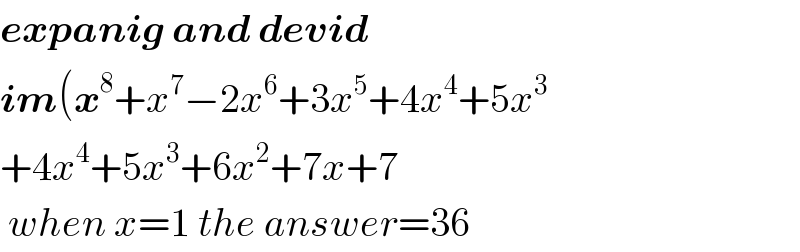
$$\boldsymbol{{expanig}}\:\boldsymbol{{and}}\:\boldsymbol{{devid}} \\ $$$$\boldsymbol{{im}}\left(\boldsymbol{{x}}^{\mathrm{8}} +{x}^{\mathrm{7}} −\mathrm{2}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{5}} +\mathrm{4}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} \right. \\ $$$$+\mathrm{4}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{7} \\ $$$$\:{when}\:{x}=\mathrm{1}\:{the}\:{answer}=\mathrm{36} \\ $$
