
Question Number 212368 by Spillover last updated on 12/Oct/24
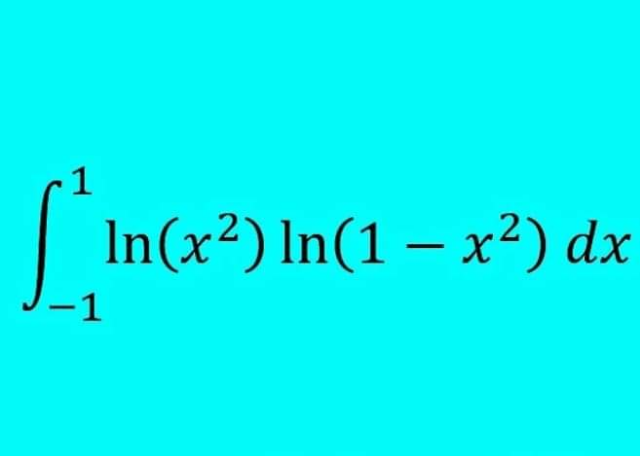
Answered by MathematicalUser2357 last updated on 13/Oct/24

$$\infty \\ $$
Commented by Ghisom last updated on 14/Oct/24

$$\mathrm{no} \\ $$
Commented by MathematicalUser2357 last updated on 04/Nov/24
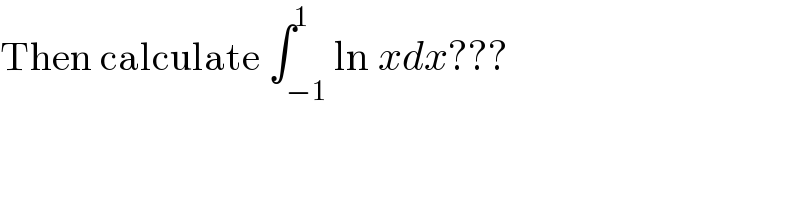
$$\mathrm{Then}\:\mathrm{calculate}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \mathrm{ln}\:{xdx}??? \\ $$
Commented by Ghisom last updated on 04/Nov/24
![∫_(−1) ^1 ln x dx=[xln x −x]_(−1) ^1 =−2+πi but here we have ∫_(−1) ^1 ln x^2 ln (1−x^2 ) dx= =16−π^2 −8ln 2 ≈.585218154431](Q213411.png)
$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\mathrm{ln}\:{x}\:{dx}=\left[{x}\mathrm{ln}\:{x}\:−{x}\right]_{−\mathrm{1}} ^{\mathrm{1}} =−\mathrm{2}+\pi\mathrm{i} \\ $$$$\mathrm{but}\:\mathrm{here}\:\mathrm{we}\:\mathrm{have} \\ $$$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\mathrm{ln}\:{x}^{\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:{dx}= \\ $$$$=\mathrm{16}−\pi^{\mathrm{2}} −\mathrm{8ln}\:\mathrm{2}\:\approx.\mathrm{585218154431} \\ $$
