
Question Number 212347 by Ismoiljon_008 last updated on 10/Oct/24
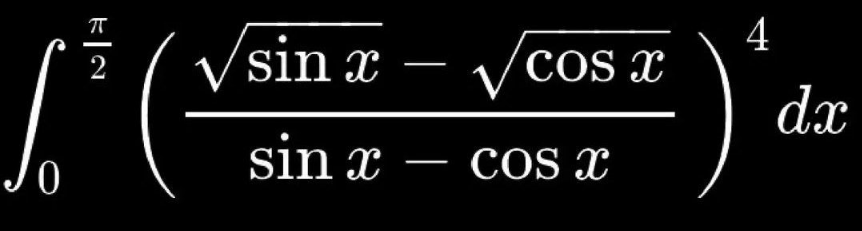
Commented by Ismoiljon_008 last updated on 10/Oct/24
$$ \\ $$$$\:\:\:\mathbb{H}{elp}\:{me},\:{please}\:. \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 10/Oct/24
![I=∫_0 ^(π/2) ((((√(sinx))−(√(cosx)))/(sinx−cosx)))^4 dx =∫_0 ^(π/2) ((((√(sinx))−(√(cosx)))/(((√(sinx))−(√(cosx)))((√(sinx))+(√(cosx))))))^4 dx =∫_0 ^(π/2) ((1/( (√(sinx))+(√(cosx)))))^4 dx=∫_0 ^(π/2) (((√(secx))/( (√(tanx))+1)))^4 dx =∫_0 ^(π/2) ((sec^2 x)/( ((√(tanx))+1)^4 ))dx=^(t=tanx) ∫_0 ^∞ (dt/(((√t)+1)^4 ))=^(t=u^2 ) 2∫_0 ^∞ (u/((u+1)^4 ))du =−[((2u)/(3(u+1)^3 ))]_0 ^∞ +(2/3)∫_0 ^∞ (du/((u+1)^3 ))=−[(1/(3(u+1)^2 ))]_0 ^∞ =(1/3)](Q212349.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\sqrt{\mathrm{sin}{x}}−\sqrt{\mathrm{cos}{x}}}{\mathrm{sin}{x}−\mathrm{cos}{x}}\right)^{\mathrm{4}} {dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\sqrt{\mathrm{sin}{x}}−\sqrt{\mathrm{cos}{x}}}{\left(\sqrt{\mathrm{sin}{x}}−\sqrt{\mathrm{cos}{x}}\right)\left(\sqrt{\mathrm{sin}{x}}+\sqrt{\mathrm{cos}{x}}\right)}\right)^{\mathrm{4}} {dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{sin}{x}}+\sqrt{\mathrm{cos}{x}}}\right)^{\mathrm{4}} {dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\sqrt{\mathrm{sec}{x}}}{\:\sqrt{\mathrm{tan}{x}}+\mathrm{1}}\right)^{\mathrm{4}} {dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} {x}}{\:\left(\sqrt{\mathrm{tan}{x}}+\mathrm{1}\right)^{\mathrm{4}} }{dx}\overset{{t}=\mathrm{tan}{x}} {=}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\sqrt{{t}}+\mathrm{1}\right)^{\mathrm{4}} }\overset{{t}={u}^{\mathrm{2}} } {=}\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{u}}{\left({u}+\mathrm{1}\right)^{\mathrm{4}} }{du} \\ $$$$\:\:=−\left[\frac{\mathrm{2}{u}}{\mathrm{3}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{3}} }=−\left[\frac{\mathrm{1}}{\mathrm{3}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by Ghisom last updated on 10/Oct/24
![∫_0 ^(π/2) ((((√(sin x))−(√(cos x)))/(sin x −cos x)))^4 dx= [t=1+(√(tan x))] =2∫_1 ^∞ ((1/t^3 )−(1/t^4 ))dt=[(2/(3t^3 ))−(1/t^2 )]_1 ^∞ =(1/3)](Q212352.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\left(\frac{\sqrt{\mathrm{sin}\:{x}}−\sqrt{\mathrm{cos}\:{x}}}{\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}}\right)^{\mathrm{4}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}\right] \\ $$$$=\mathrm{2}\underset{\mathrm{1}} {\overset{\infty} {\int}}\left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\right){dt}=\left[\frac{\mathrm{2}}{\mathrm{3}{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$
