
Question Number 212341 by Spillover last updated on 10/Oct/24
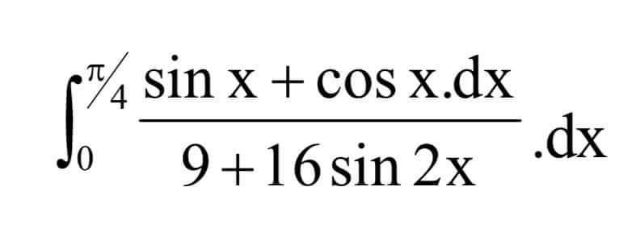
Answered by Ghisom last updated on 10/Oct/24
![∫_0 ^(π/4) ((sin x +cos x)/(9+16sin 2x))dx= [t=((4(√2))/5)cos (x+(π/4))] =−(1/(20))∫_0 ^(4/5) (dt/(t^2 −1))=−(1/(40))[ln ∣((t−1)/(t+1))∣]_ =((ln 3)/(20))](Q212351.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{9}+\mathrm{16sin}\:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{5}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{20}}\underset{\mathrm{0}} {\overset{\mathrm{4}/\mathrm{5}} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{40}}\left[\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\right]_{} =\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{20}} \\ $$
Commented by Spillover last updated on 12/Oct/24

$${great} \\ $$
Answered by MathematicalUser2357 last updated on 13/Oct/24
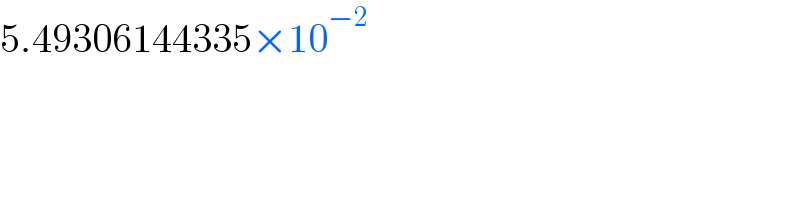
$$\mathrm{5}.\mathrm{49306144335}×\mathrm{10}^{−\mathrm{2}} \\ $$
