
Question Number 212181 by RojaTaniya last updated on 05/Oct/24
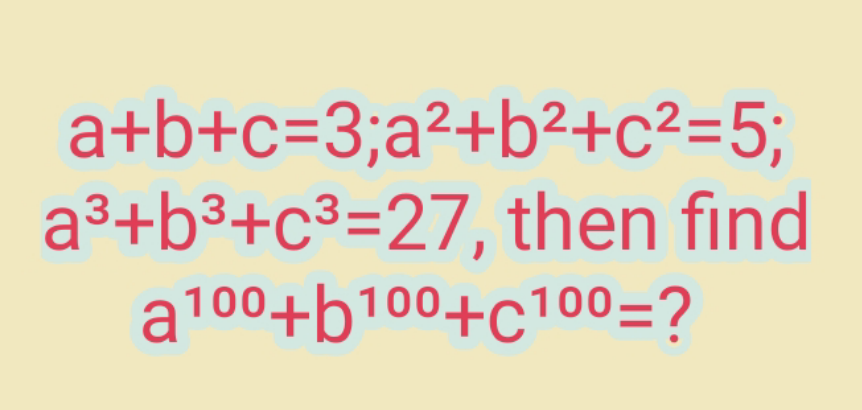
Answered by A5T last updated on 05/Oct/24
![a^2 +b^2 +c^2 =(a+b+c)^2 −2(ab+bc+ca)=5 ⇒ab+bc+ca=2 a^3 +b^3 +c^3 −3abc=(a+b+c)[(a+b+c)^2 −3(ab+bc+ca)] ⇒27−3abc=3[9−3(2)]=9⇒abc=6 ⇒a,b,c are roots of x^3 −3x^2 +2x−6=0 ⇒x^2 (x−3)+2(x−3)=(x−3)(x^2 +2)=0 (a,b,c)=(3,i(√2),−i(√2)) upto permutation ⇒a^(100) +b^(100) +c^(100) =3^(100) +2^(50) +2^(50) =3^(100) +2^(51)](Q212184.png)
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{5} \\ $$$$\Rightarrow{ab}+{bc}+{ca}=\mathrm{2} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}=\left({a}+{b}+{c}\right)\left[\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{3}\left({ab}+{bc}+{ca}\right)\right] \\ $$$$\Rightarrow\mathrm{27}−\mathrm{3}{abc}=\mathrm{3}\left[\mathrm{9}−\mathrm{3}\left(\mathrm{2}\right)\right]=\mathrm{9}\Rightarrow{abc}=\mathrm{6} \\ $$$$\Rightarrow{a},{b},{c}\:{are}\:{roots}\:{of}\:{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left({x}−\mathrm{3}\right)+\mathrm{2}\left({x}−\mathrm{3}\right)=\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{3},{i}\sqrt{\mathrm{2}},−{i}\sqrt{\mathrm{2}}\right)\:{upto}\:{permutation} \\ $$$$\Rightarrow{a}^{\mathrm{100}} +{b}^{\mathrm{100}} +{c}^{\mathrm{100}} =\mathrm{3}^{\mathrm{100}} +\mathrm{2}^{\mathrm{50}} +\mathrm{2}^{\mathrm{50}} =\mathrm{3}^{\mathrm{100}} +\mathrm{2}^{\mathrm{51}} \\ $$
Commented by RojaTaniya last updated on 05/Oct/24

$${Sir}\:{thanks} \\ $$
Answered by mr W last updated on 10/Oct/24
![p_1 =e_1 =3 p_2 =e_1 p_1 −2e_2 =5 ⇒e_2 =2 p_3 =e_1 p_2 −e_2 p_1 +3e_3 =27 ⇒e_3 =6 p_n =e_1 p_(n−1) −e_2 p_(n−2) +e_3 p_(n−3) r^3 −3r^2 +2r−6=0 r_1 =3, r_(2,3) =±(√2)i p_n =3^n +2^(n/2) [i^n +(−i)^n ]=3^n +2^((n/2)+1) cos ((nπ)/2) ⇒p_(100) =3^(100) +2^(51)](Q212198.png)
$${p}_{\mathrm{1}} ={e}_{\mathrm{1}} =\mathrm{3} \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} =\mathrm{5}\:\Rightarrow{e}_{\mathrm{2}} =\mathrm{2} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} +\mathrm{3}{e}_{\mathrm{3}} =\mathrm{27}\:\Rightarrow{e}_{\mathrm{3}} =\mathrm{6} \\ $$$${p}_{{n}} ={e}_{\mathrm{1}} {p}_{{n}−\mathrm{1}} −{e}_{\mathrm{2}} {p}_{{n}−\mathrm{2}} +{e}_{\mathrm{3}} {p}_{{n}−\mathrm{3}} \\ $$$${r}^{\mathrm{3}} −\mathrm{3}{r}^{\mathrm{2}} +\mathrm{2}{r}−\mathrm{6}=\mathrm{0} \\ $$$${r}_{\mathrm{1}} =\mathrm{3},\:{r}_{\mathrm{2},\mathrm{3}} =\pm\sqrt{\mathrm{2}}{i} \\ $$$${p}_{{n}} =\mathrm{3}^{{n}} +\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \left[{i}^{{n}} +\left(−{i}\right)^{{n}} \right]=\mathrm{3}^{{n}} +\mathrm{2}^{\frac{{n}}{\mathrm{2}}+\mathrm{1}} \mathrm{cos}\:\frac{{n}\pi}{\mathrm{2}} \\ $$$$\Rightarrow{p}_{\mathrm{100}} =\mathrm{3}^{\mathrm{100}} +\mathrm{2}^{\mathrm{51}} \\ $$
Commented by TonyCWX08 last updated on 08/Oct/24

$${Girand}−{Newton}'{s}\:{Identity}? \\ $$
Commented by mr W last updated on 08/Oct/24

$${yes} \\ $$
