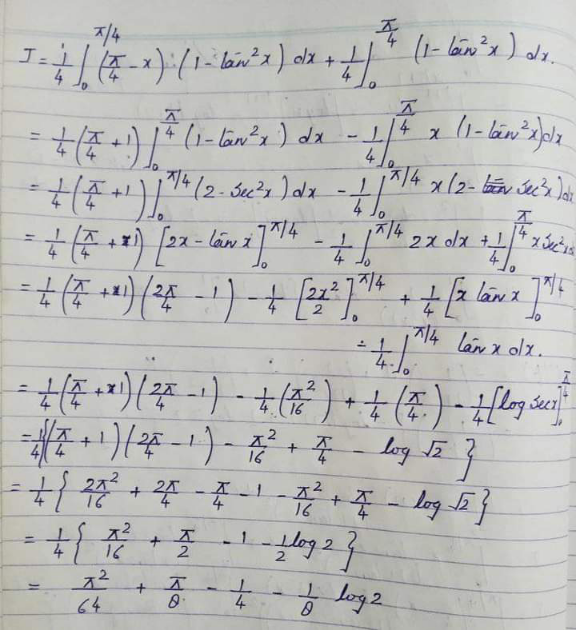Question Number 212023 by Spillover last updated on 27/Sep/24
Answered by Frix last updated on 27/Sep/24
![∫ (((x+1)tan x)/((1+tan x)^2 ))dx= =(1/2)∫(x+1−(1/(1+sin 2x_([t=tan x]) ))−(x/(1+sin 2x_([by parts]) )))dx= ... =((x(x+1))/4)+(((x+1))/(2(1+tan x)))+(1/8)ln ((1+tan^2 x)/((1+tan x)^2 )) +C ∫_0 ^(π/4) (((x+1)tan x)/((1+tan x)^2 ))dx=(π^2 /(64))+(π/8)−(1/4)−((ln 2)/8) [∫_0 ^(π/2) (((x+1)tan x)/((1+tan x)^2 ))dx=(π^2 /(16))+(π/8)−(1/2)]](Q212031.png)
$$\int\:\frac{\left({x}+\mathrm{1}\right)\mathrm{tan}\:{x}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left({x}+\mathrm{1}−\frac{\mathrm{1}}{\underset{\left[{t}=\mathrm{tan}\:{x}\right]} {\underbrace{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}}}}−\frac{{x}}{\underset{\left[\mathrm{by}\:\mathrm{parts}\right]} {\underbrace{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}}}}\right){dx}= \\ $$$$... \\ $$$$=\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{4}}+\frac{\left({x}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{tan}\:{x}\right)}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\:\frac{\left({x}+\mathrm{1}\right)\mathrm{tan}\:{x}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{64}}+\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{8}} \\ $$$$ \\ $$$$\left[\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\left({x}+\mathrm{1}\right)\mathrm{tan}\:{x}}{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$
Commented by Spillover last updated on 27/Sep/24

$${correct} \\ $$
Answered by Spillover last updated on 27/Sep/24
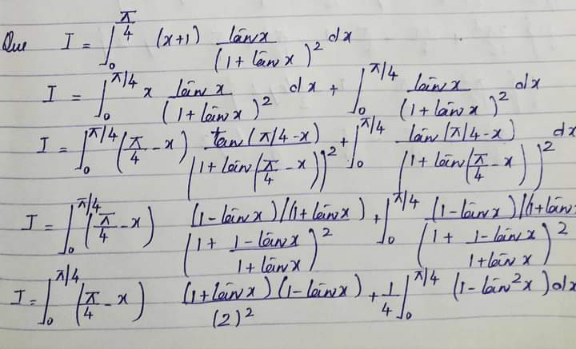
Answered by Spillover last updated on 27/Sep/24