
Question Number 211979 by Spillover last updated on 25/Sep/24
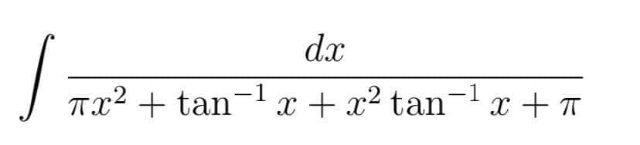
Answered by BHOOPENDRA last updated on 25/Sep/24
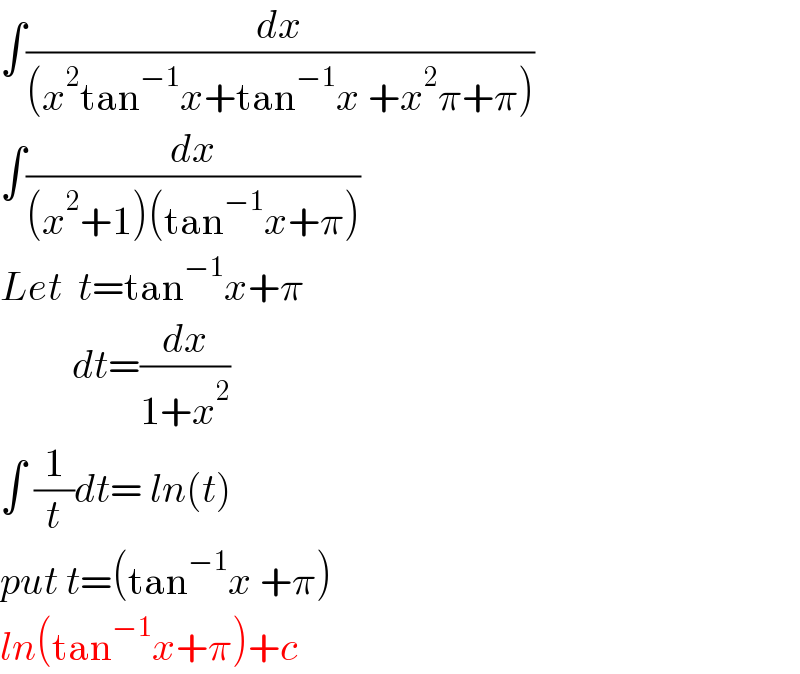
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} {x}+\mathrm{tan}^{−\mathrm{1}} {x}\:+{x}^{\mathrm{2}} \pi+\pi\right)} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{tan}^{−\mathrm{1}} {x}+\pi\right)} \\ $$$${Let}\:\:{t}=\mathrm{tan}^{−\mathrm{1}} {x}+\pi \\ $$$$\:\:\:\:\:\:\:\:\:{dt}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\int\:\frac{\mathrm{1}}{{t}}{dt}=\:{ln}\left({t}\right)\: \\ $$$${put}\:{t}=\left(\mathrm{tan}^{−\mathrm{1}} {x}\:+\pi\right) \\ $$$${ln}\left(\mathrm{tan}^{−\mathrm{1}} {x}+\pi\right)+{c} \\ $$
Commented by Spillover last updated on 26/Sep/24
$${great}.{thanks} \\ $$
