
Question Number 211920 by Spillover last updated on 24/Sep/24

Answered by aleks041103 last updated on 24/Sep/24
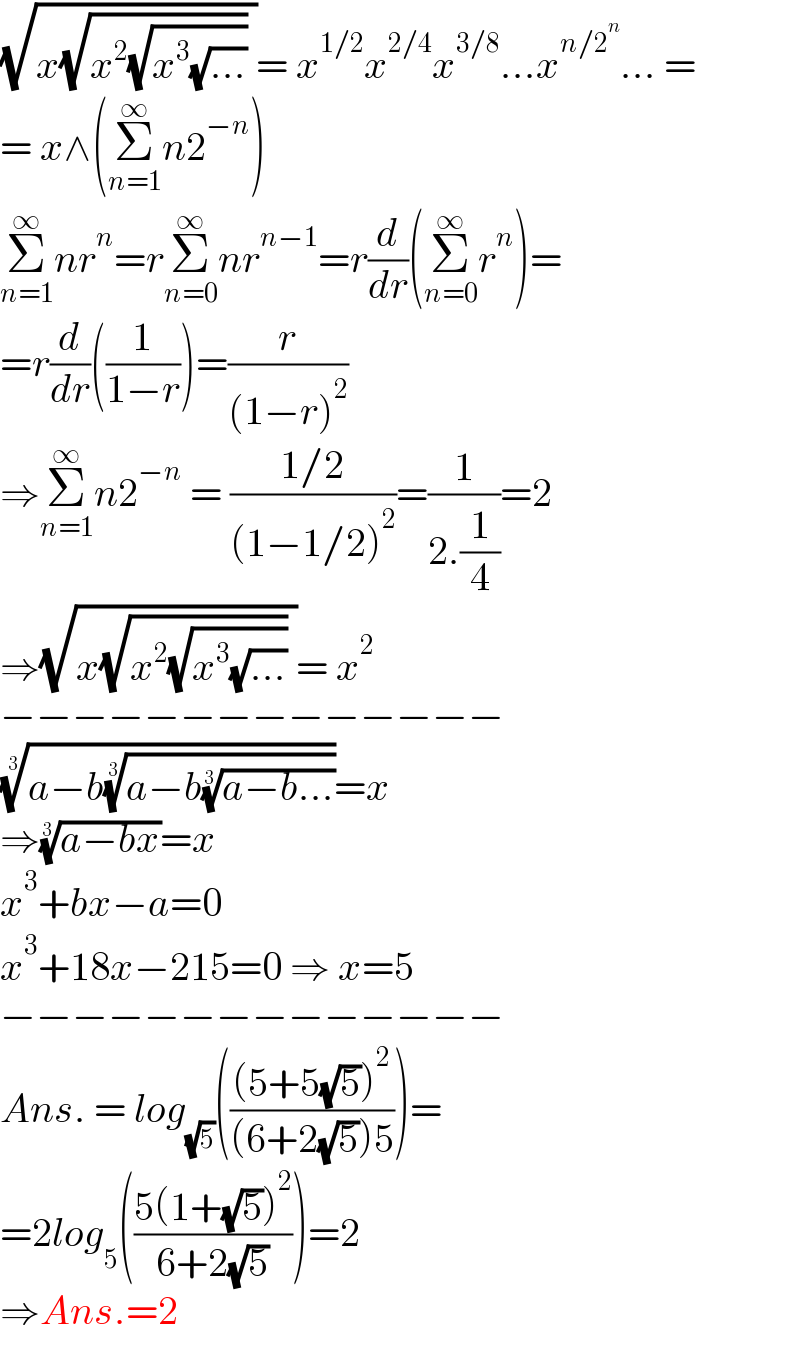
$$\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{...}}}\:}=\:{x}^{\mathrm{1}/\mathrm{2}} {x}^{\mathrm{2}/\mathrm{4}} {x}^{\mathrm{3}/\mathrm{8}} ...{x}^{{n}/\mathrm{2}^{{n}} } ...\:= \\ $$$$=\:{x}\wedge\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}\mathrm{2}^{−{n}} \right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nr}^{{n}} ={r}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{nr}^{{n}−\mathrm{1}} ={r}\frac{{d}}{{dr}}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{r}^{{n}} \right)= \\ $$$$={r}\frac{{d}}{{dr}}\left(\frac{\mathrm{1}}{\mathrm{1}−{r}}\right)=\frac{{r}}{\left(\mathrm{1}−{r}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}\mathrm{2}^{−{n}} \:=\:\frac{\mathrm{1}/\mathrm{2}}{\left(\mathrm{1}−\mathrm{1}/\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{2} \\ $$$$\Rightarrow\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{...}}}\:}=\:{x}^{\mathrm{2}} \\ $$$$−−−−−−−−−−−−−− \\ $$$$\sqrt[{\mathrm{3}}]{{a}−{b}\sqrt[{\mathrm{3}}]{{a}−{b}\sqrt[{\mathrm{3}}]{{a}−{b}...}}}={x} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{{a}−{bx}}={x} \\ $$$${x}^{\mathrm{3}} +{bx}−{a}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +\mathrm{18}{x}−\mathrm{215}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{5} \\ $$$$−−−−−−−−−−−−−− \\ $$$${Ans}.\:=\:{log}_{\sqrt{\mathrm{5}}} \left(\frac{\left(\mathrm{5}+\mathrm{5}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)\mathrm{5}}\right)= \\ $$$$=\mathrm{2}{log}_{\mathrm{5}} \left(\frac{\mathrm{5}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}\right)=\mathrm{2} \\ $$$$\Rightarrow{Ans}.=\mathrm{2} \\ $$
Commented by Spillover last updated on 25/Sep/24
$${great}.{thanks} \\ $$
