Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 211917 by Spillover last updated on 24/Sep/24

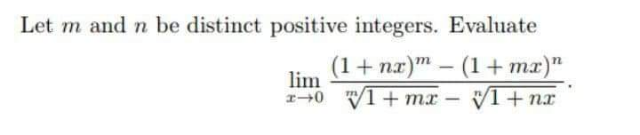
Answered by BHOOPENDRA last updated on 24/Sep/24

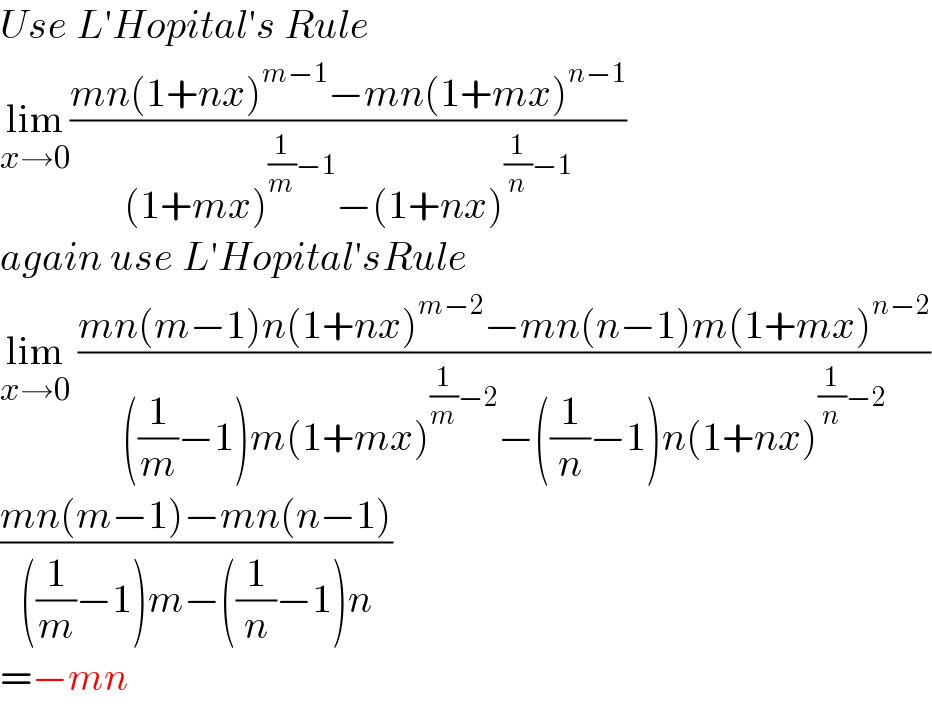
Use L′Hopital′s Rule lim_(x→0) ((mn(1+nx)^(m−1) −mn(1+mx)^(n−1) )/((1+mx)^((1/m)−1) −(1+nx)^((1/n)−1) )) again use L′Hopital′sRule lim_(x→0) ((mn(m−1)n(1+nx)^(m−2) −mn(n−1)m(1+mx)^(n−2) )/(((1/m)−1)m(1+mx)^((1/m)−2) −((1/n)−1)n(1+nx)^((1/n)−2) )) ((mn(m−1)−mn(n−1))/(((1/m)−1)m−((1/n)−1)n)) =−mn

$${Use}\:{L}'{Hopital}'{s}\:{Rule}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{mn}\left(\mathrm{1}+{nx}\right)^{{m}−\mathrm{1}} −{mn}\left(\mathrm{1}+{mx}\right)^{{n}−\mathrm{1}} }{\left(\mathrm{1}+{mx}\right)^{\frac{\mathrm{1}}{{m}}−\mathrm{1}} −\left(\mathrm{1}+{nx}\right)^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} } \\ $$$${again}\:{use}\:{L}'{Hopital}'{sRule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{mn}\left({m}−\mathrm{1}\right){n}\left(\mathrm{1}+{nx}\right)^{{m}−\mathrm{2}} −{mn}\left({n}−\mathrm{1}\right){m}\left(\mathrm{1}+{mx}\right)^{{n}−\mathrm{2}} }{\left(\frac{\mathrm{1}}{{m}}−\mathrm{1}\right){m}\left(\mathrm{1}+{mx}\right)^{\frac{\mathrm{1}}{{m}}−\mathrm{2}} −\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right){n}\left(\mathrm{1}+{nx}\right)^{\frac{\mathrm{1}}{{n}}−\mathrm{2}} } \\ $$$$\frac{{mn}\left({m}−\mathrm{1}\right)−{mn}\left({n}−\mathrm{1}\right)}{\left(\frac{\mathrm{1}}{{m}}−\mathrm{1}\right){m}−\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right){n}} \\ $$$$=−{mn} \\ $$

Commented by Spillover last updated on 24/Sep/24

great.thanks

$${great}.{thanks} \\ $$

Answered by BHOOPENDRA last updated on 24/Sep/24

method(II) (1+nx)^m =1+mnx+o(x^2 ) (1+mx)^n =1+nmx+o(x^2 ) So (1+nx)^m −(1+mx)^n =0 for second order term (1+nx)^n =1+mnx+((m(m−1))/2)(nx)^2 +o(x^3 ) (1+mx)^n =1+mnx +((n(n−1))/2)(mx)^2 +o(x^3 ) (1+nx)^n −(1+mx)^m =((m(m−1))/2)(nx)^2 −((n(n−1))/2)(mx)^2 similarly do for denominator lim_(x→0) ((((m(m−1))/2)(nx)^2 −((n(n−1))/2)(mx)^2 )/((((m−1))/(2m))(mx)^2 −((n(n−1))/(2n))(nx)^2 )) =−mn

$${method}\left({II}\right) \\ $$$$\left(\mathrm{1}+{nx}\right)^{{m}} =\mathrm{1}+{mnx}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{1}+{mx}\right)^{{n}} =\mathrm{1}+{nmx}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${So}\: \\ $$$$\left(\mathrm{1}+{nx}\right)^{{m}} −\left(\mathrm{1}+{mx}\right)^{{n}} =\mathrm{0} \\ $$$${for}\:{second}\:{order}\:{term} \\ $$$$\left(\mathrm{1}+{nx}\right)^{{n}} =\mathrm{1}+{mnx}+\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}\left({nx}\right)^{\mathrm{2}} +{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\left(\mathrm{1}+{mx}\right)^{{n}} =\mathrm{1}+{mnx}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left({mx}\right)^{\mathrm{2}} +{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\left(\mathrm{1}+{nx}\right)^{{n}} −\left(\mathrm{1}+{mx}\right)^{{m}} =\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}\left({nx}\right)^{\mathrm{2}} −\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left({mx}\right)^{\mathrm{2}} \\ $$$${similarly}\:{do}\:{for}\:{denominator} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}\left({nx}\right)^{\mathrm{2}} −\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left({mx}\right)^{\mathrm{2}} }{\frac{\left({m}−\mathrm{1}\right)}{\mathrm{2}{m}}\left({mx}\right)^{\mathrm{2}} −\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}}\left({nx}\right)^{\mathrm{2}} } \\ $$$$=−{mn} \\ $$

Commented by Spillover last updated on 24/Sep/24

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com