Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 211732 by BaliramKumar last updated on 19/Sep/24

Answered by TonyCWX08 last updated on 19/Sep/24

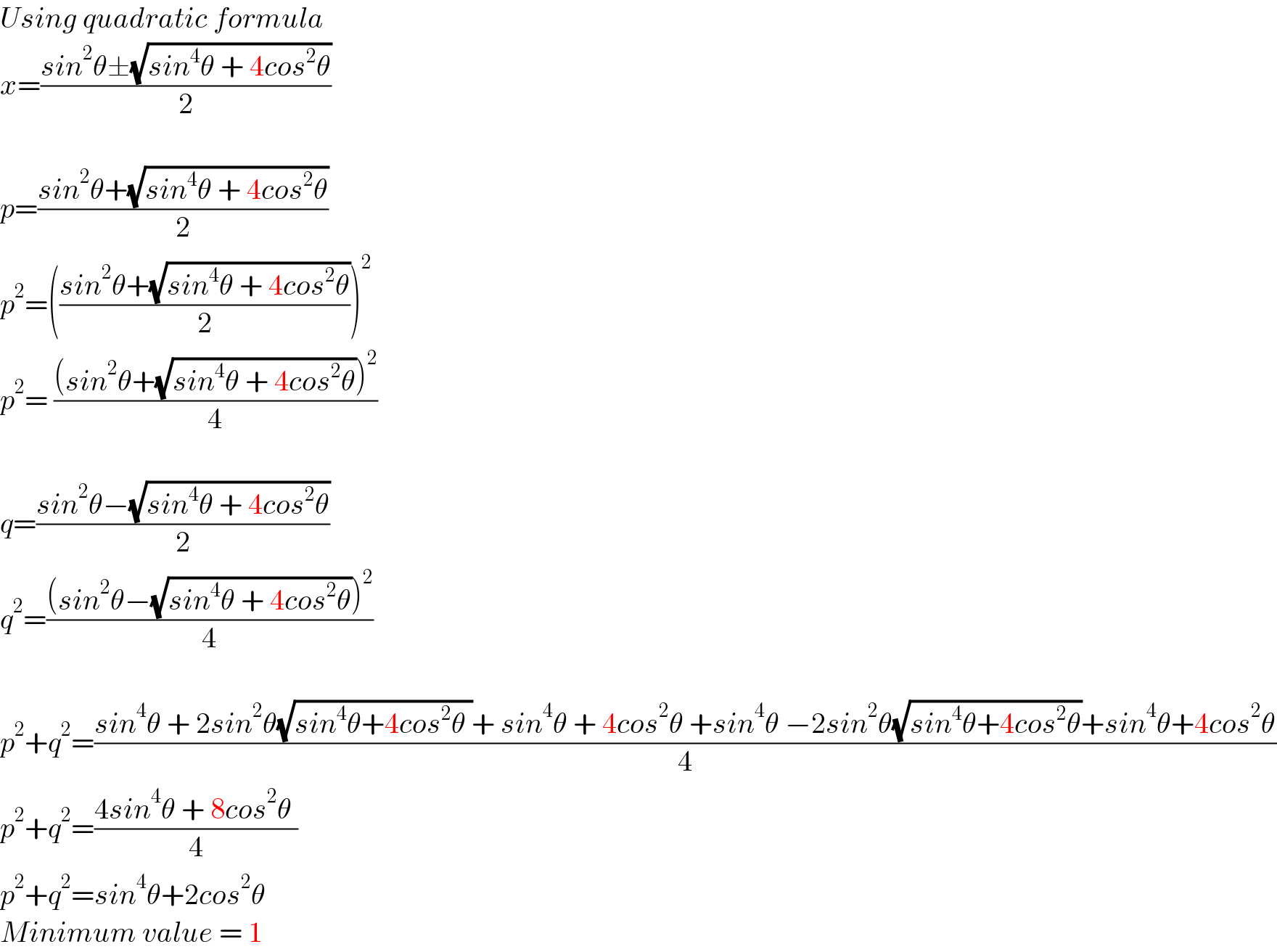
Using quadratic formula x=((sin^2 θ±(√(sin^4 θ + 4cos^2 θ)))/2) p=((sin^2 θ+(√(sin^4 θ + 4cos^2 θ)))/2) p^2 =(((sin^2 θ+(√(sin^4 θ + 4cos^2 θ)))/2))^2 p^2 = (((sin^2 θ+(√(sin^4 θ + 4cos^2 θ)))^2 )/4) q=((sin^2 θ−(√(sin^4 θ + 4cos^2 θ)))/2) q^2 =(((sin^2 θ−(√(sin^4 θ + 4cos^2 θ)))^2 )/4) p^2 +q^2 =((sin^4 θ + 2sin^2 θ(√(sin^4 θ+4cos^2 θ ))+ sin^4 θ + 4cos^2 θ +sin^4 θ −2sin^2 θ(√(sin^4 θ+4cos^2 θ))+sin^4 θ+4cos^2 θ)/4) p^2 +q^2 =((4sin^4 θ + 8cos^2 θ )/4) p^2 +q^2 =sin^4 θ+2cos^2 θ Minimum value = 1

$${Using}\:{quadratic}\:{formula} \\ $$$${x}=\frac{{sin}^{\mathrm{2}} \theta\pm\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}}{\mathrm{2}} \\ $$$$ \\ $$$${p}=\frac{{sin}^{\mathrm{2}} \theta+\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}}{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} =\left(\frac{{sin}^{\mathrm{2}} \theta+\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} =\:\frac{\left({sin}^{\mathrm{2}} \theta+\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$$${q}=\frac{{sin}^{\mathrm{2}} \theta−\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}}{\mathrm{2}} \\ $$$${q}^{\mathrm{2}} =\frac{\left({sin}^{\mathrm{2}} \theta−\sqrt{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\frac{{sin}^{\mathrm{4}} \theta\:+\:\mathrm{2}{sin}^{\mathrm{2}} \theta\sqrt{{sin}^{\mathrm{4}} \theta+\mathrm{4}{cos}^{\mathrm{2}} \theta\:}+\:{sin}^{\mathrm{4}} \theta\:+\:\mathrm{4}{cos}^{\mathrm{2}} \theta\:+{sin}^{\mathrm{4}} \theta\:−\mathrm{2}{sin}^{\mathrm{2}} \theta\sqrt{{sin}^{\mathrm{4}} \theta+\mathrm{4}{cos}^{\mathrm{2}} \theta}+{sin}^{\mathrm{4}} \theta+\mathrm{4}{cos}^{\mathrm{2}} \theta}{\mathrm{4}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\frac{\mathrm{4}{sin}^{\mathrm{4}} \theta\:+\:\mathrm{8}{cos}^{\mathrm{2}} \theta\:}{\mathrm{4}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} ={sin}^{\mathrm{4}} \theta+\mathrm{2}{cos}^{\mathrm{2}} \theta \\ $$$${Minimum}\:{value}\:=\:\mathrm{1} \\ $$

Commented by BaliramKumar last updated on 19/Sep/24

first step 4cos^2 θ

$${first}\:{step}\:\mathrm{4}{cos}^{\mathrm{2}} \theta \\ $$

Commented by TonyCWX08 last updated on 19/Sep/24

Edited

$${Edited} \\ $$

Answered by BHOOPENDRA last updated on 19/Sep/24

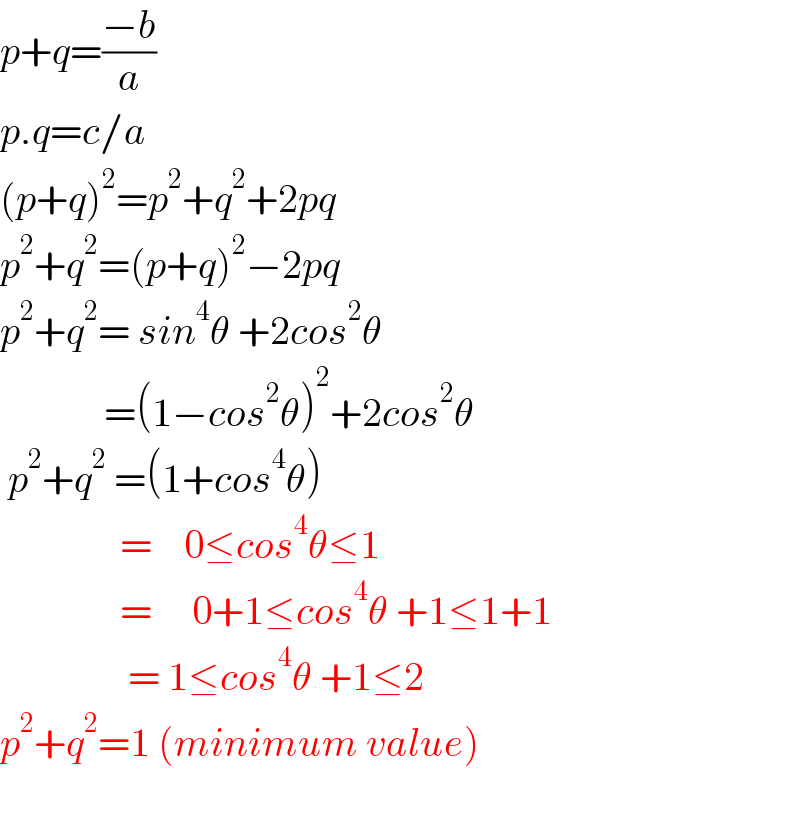
p+q=((−b)/a) p.q=c/a (p+q)^2 =p^2 +q^2 +2pq p^2 +q^2 =(p+q)^2 −2pq p^2 +q^2 = sin^4 θ +2cos^2 θ =(1−cos^2 θ)^2 +2cos^2 θ p^2 +q^2 =(1+cos^4 θ) = 0≤cos^4 θ≤1 = 0+1≤cos^4 θ +1≤1+1 = 1≤cos^4 θ +1≤2 p^2 +q^2 =1 (minimum value)

$${p}+{q}=\frac{−{b}}{{a}} \\ $$$${p}.{q}={c}/{a} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{2}{pq} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\:{sin}^{\mathrm{4}} \theta\:+\mathrm{2}{cos}^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)^{\mathrm{2}} +\mathrm{2}{cos}^{\mathrm{2}} \theta \\ $$$$\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} \:=\left(\mathrm{1}+{cos}^{\mathrm{4}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\mathrm{0}\leq{cos}^{\mathrm{4}} \theta\leq\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\mathrm{0}+\mathrm{1}\leq{cos}^{\mathrm{4}} \theta\:+\mathrm{1}\leq\mathrm{1}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\leq{cos}^{\mathrm{4}} \theta\:+\mathrm{1}\leq\mathrm{2} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{1}\:\left({minimum}\:{value}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com