Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 211437 by necx122 last updated on 09/Sep/24

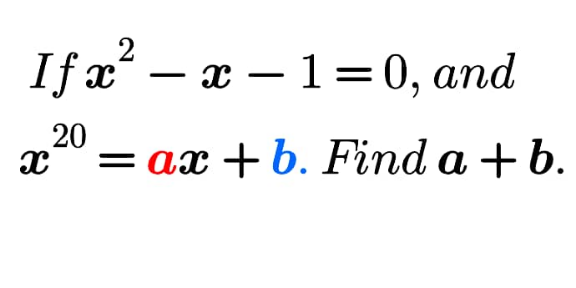
Commented by AlagaIbile last updated on 09/Sep/24

I posted the question on Cowbellpedia Whatshapp group two hours ago. How did it reach here?

$$\:\:{I}\:{posted}\:{the}\:{question}\:{on}\: \\ $$$$\:{Cowbellpedia}\:{Whatshapp}\:{group}\:\:{two} \\ $$$$\:{hours}\:{ago}.\:{How}\:{did}\:{it}\:{reach}\:{here}? \\ $$

Answered by A5T last updated on 09/Sep/24

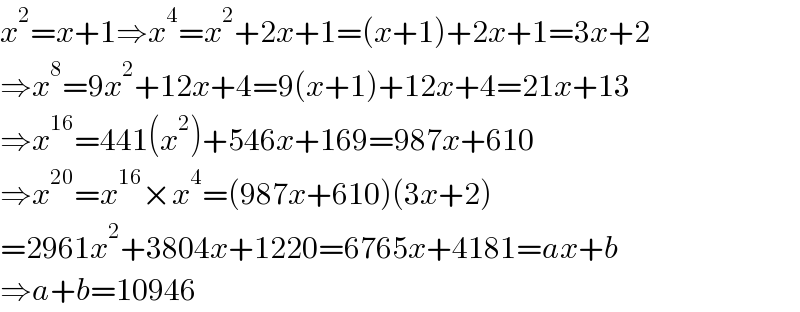
x^2 =x+1⇒x^4 =x^2 +2x+1=(x+1)+2x+1=3x+2 ⇒x^8 =9x^2 +12x+4=9(x+1)+12x+4=21x+13 ⇒x^(16) =441(x^2 )+546x+169=987x+610 ⇒x^(20) =x^(16) ×x^4 =(987x+610)(3x+2) =2961x^2 +3804x+1220=6765x+4181=ax+b ⇒a+b=10946

$${x}^{\mathrm{2}} ={x}+\mathrm{1}\Rightarrow{x}^{\mathrm{4}} ={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}=\left({x}+\mathrm{1}\right)+\mathrm{2}{x}+\mathrm{1}=\mathrm{3}{x}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{8}} =\mathrm{9}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{4}=\mathrm{9}\left({x}+\mathrm{1}\right)+\mathrm{12}{x}+\mathrm{4}=\mathrm{21}{x}+\mathrm{13} \\ $$$$\Rightarrow{x}^{\mathrm{16}} =\mathrm{441}\left({x}^{\mathrm{2}} \right)+\mathrm{546}{x}+\mathrm{169}=\mathrm{987}{x}+\mathrm{610} \\ $$$$\Rightarrow{x}^{\mathrm{20}} ={x}^{\mathrm{16}} ×{x}^{\mathrm{4}} =\left(\mathrm{987}{x}+\mathrm{610}\right)\left(\mathrm{3}{x}+\mathrm{2}\right) \\ $$$$=\mathrm{2961}{x}^{\mathrm{2}} +\mathrm{3804}{x}+\mathrm{1220}=\mathrm{6765}{x}+\mathrm{4181}={ax}+{b} \\ $$$$\Rightarrow{a}+{b}=\mathrm{10946} \\ $$

Answered by Rasheed.Sindhi last updated on 09/Sep/24

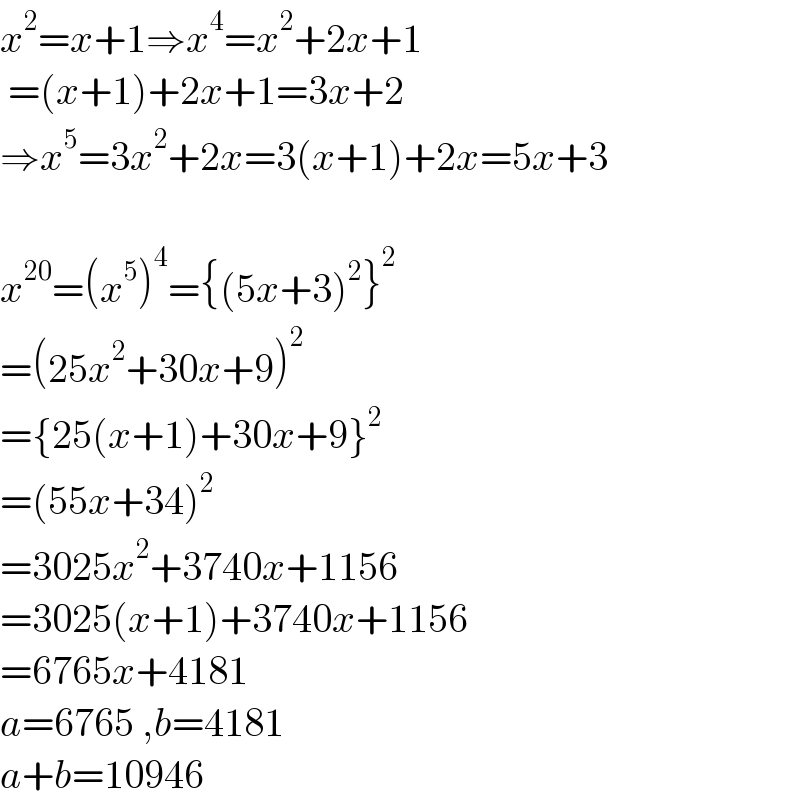
x^2 =x+1⇒x^4 =x^2 +2x+1 =(x+1)+2x+1=3x+2 ⇒x^5 =3x^2 +2x=3(x+1)+2x=5x+3 x^(20) =(x^5 )^4 ={(5x+3)^2 }^2 =(25x^2 +30x+9)^2 ={25(x+1)+30x+9}^2 =(55x+34)^2 =3025x^2 +3740x+1156 =3025(x+1)+3740x+1156 =6765x+4181 a=6765 ,b=4181 a+b=10946

$${x}^{\mathrm{2}} ={x}+\mathrm{1}\Rightarrow{x}^{\mathrm{4}} ={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$$\:=\left({x}+\mathrm{1}\right)+\mathrm{2}{x}+\mathrm{1}=\mathrm{3}{x}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}=\mathrm{3}\left({x}+\mathrm{1}\right)+\mathrm{2}{x}=\mathrm{5}{x}+\mathrm{3} \\ $$$$\: \\ $$$${x}^{\mathrm{20}} =\left({x}^{\mathrm{5}} \right)^{\mathrm{4}} =\left\{\left(\mathrm{5}{x}+\mathrm{3}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$=\left(\mathrm{25}{x}^{\mathrm{2}} +\mathrm{30}{x}+\mathrm{9}\right)^{\mathrm{2}} \\ $$$$=\left\{\mathrm{25}\left({x}+\mathrm{1}\right)+\mathrm{30}{x}+\mathrm{9}\right\}^{\mathrm{2}} \\ $$$$=\left(\mathrm{55}{x}+\mathrm{34}\right)^{\mathrm{2}} \\ $$$$=\mathrm{3025}{x}^{\mathrm{2}} +\mathrm{3740}{x}+\mathrm{1156} \\ $$$$=\mathrm{3025}\left({x}+\mathrm{1}\right)+\mathrm{3740}{x}+\mathrm{1156} \\ $$$$=\mathrm{6765}{x}+\mathrm{4181} \\ $$$${a}=\mathrm{6765}\:,{b}=\mathrm{4181} \\ $$$${a}+{b}=\mathrm{10946} \\ $$

Commented by necx122 last updated on 09/Sep/24

Thid id great

$${Thid}\:{id}\:{great} \\ $$

Answered by A5T last updated on 09/Sep/24

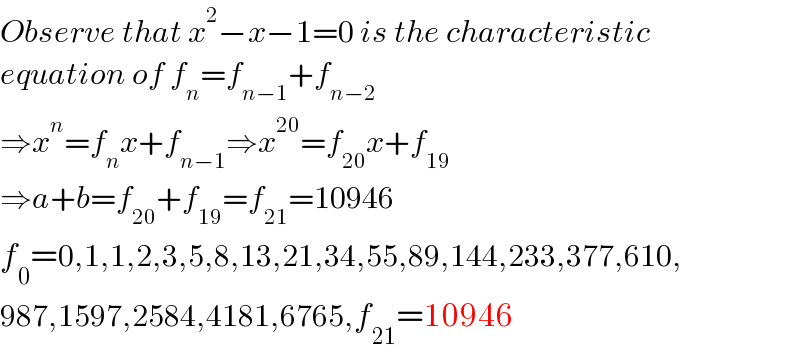
Observe that x^2 −x−1=0 is the characteristic equation of f_n =f_(n−1) +f_(n−2) ⇒x^n =f_n x+f_(n−1) ⇒x^(20) =f_(20) x+f_(19) ⇒a+b=f_(20) +f_(19) =f_(21) =10946 f_0 =0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610, 987,1597,2584,4181,6765,f_(21) =10946

$${Observe}\:{that}\:{x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0}\:{is}\:{the}\:{characteristic} \\ $$$${equation}\:{of}\:{f}_{{n}} ={f}_{{n}−\mathrm{1}} +{f}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{x}^{{n}} ={f}_{{n}} {x}+{f}_{{n}−\mathrm{1}} \Rightarrow{x}^{\mathrm{20}} ={f}_{\mathrm{20}} {x}+{f}_{\mathrm{19}} \\ $$$$\Rightarrow{a}+{b}={f}_{\mathrm{20}} +{f}_{\mathrm{19}} ={f}_{\mathrm{21}} =\mathrm{10946} \\ $$$${f}_{\mathrm{0}} =\mathrm{0},\mathrm{1},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{8},\mathrm{13},\mathrm{21},\mathrm{34},\mathrm{55},\mathrm{89},\mathrm{144},\mathrm{233},\mathrm{377},\mathrm{610}, \\ $$$$\mathrm{987},\mathrm{1597},\mathrm{2584},\mathrm{4181},\mathrm{6765},{f}_{\mathrm{21}} =\mathrm{10946} \\ $$

Commented by necx122 last updated on 09/Sep/24

hmmm.. never knew this. Cool stuff.

$${hmmm}..\:{never}\:{knew}\:{this}.\:{Cool}\:{stuff}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com