
Question Number 211418 by peter frank last updated on 08/Sep/24

Answered by Spillover last updated on 09/Sep/24
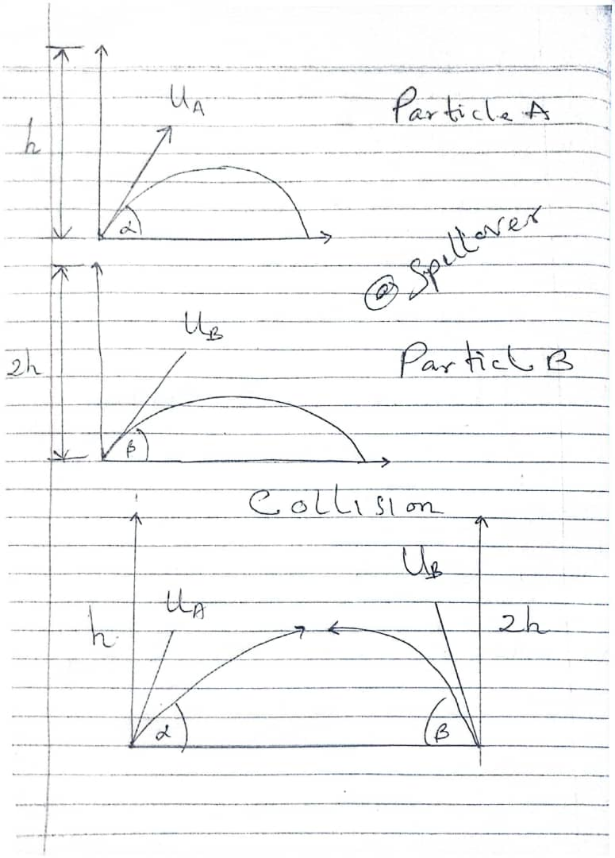
Answered by Spillover last updated on 10/Sep/24

$${Particle}\:\:{A}\: \\ $$$${Horizontal}\:{distance},\:{x}_{{A}} ={U}_{{A}} {t}\mathrm{cos}\:\alpha \\ $$$${Vertical}\:{distance}\:,{y}_{{A}} ={h}+{U}_{{A}} {t}\mathrm{sin}\:\alpha−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${Particle}\:\:{B}\: \\ $$$${Horizontal}\:{distance},\:{x}_{{B}} =\mathrm{2}{h}+{U}_{{B}} {t}\mathrm{cos}\:\beta \\ $$$${Vertical}\:{distance}\:,{y}_{{B}} ={h}+{U}_{{B}} {t}\mathrm{sin}\:\beta−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${Collision} \\ $$$$\:{x}_{{A}} ={U}_{{A}} {t}\mathrm{cos}\:\alpha=\:{x}_{{B}} =\mathrm{2}{h}+{U}_{{B}} {t}\mathrm{cos}\:\beta \\ $$$${t}=\frac{\mathrm{2}{h}}{{U}_{{A}} \mathrm{cos}\:\alpha−{U}_{{B}} \mathrm{cos}\:\beta} \\ $$$${h}+{U}_{{A}} {t}\mathrm{sin}\:\alpha−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} ={h}+{U}_{{B}} {t}\mathrm{sin}\:\beta−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${h}={t}\left({U}_{{B}} \mathrm{sin}\:{B}−{U}_{{A}} \mathrm{sin}\:\alpha\right) \\ $$$${h}=\frac{\mathrm{2}{h}\left({U}_{{B}} \mathrm{sin}\:{B}−{U}_{{A}} \mathrm{sin}\:\alpha\right)}{{U}_{{A}} \mathrm{cos}\:\alpha−{U}_{{B}} \mathrm{cos}\:\beta}. \\ $$$${U}_{{A}} \mathrm{cos}\:\alpha−{U}_{{B}} \mathrm{cos}\:\beta=\left({U}_{{B}} \mathrm{sin}\:{B}−{U}_{{A}} \mathrm{sin}\:\alpha\right) \\ $$$$\frac{{U}_{{A}} }{{U}_{{B}} }=\frac{\left(\mathrm{co}{s}\alpha+\mathrm{2sin}\:\alpha\right)}{=\left(\mathrm{cos}\:\beta+\mathrm{2sin}\:\beta\right)} \\ $$$$ \\ $$
