Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

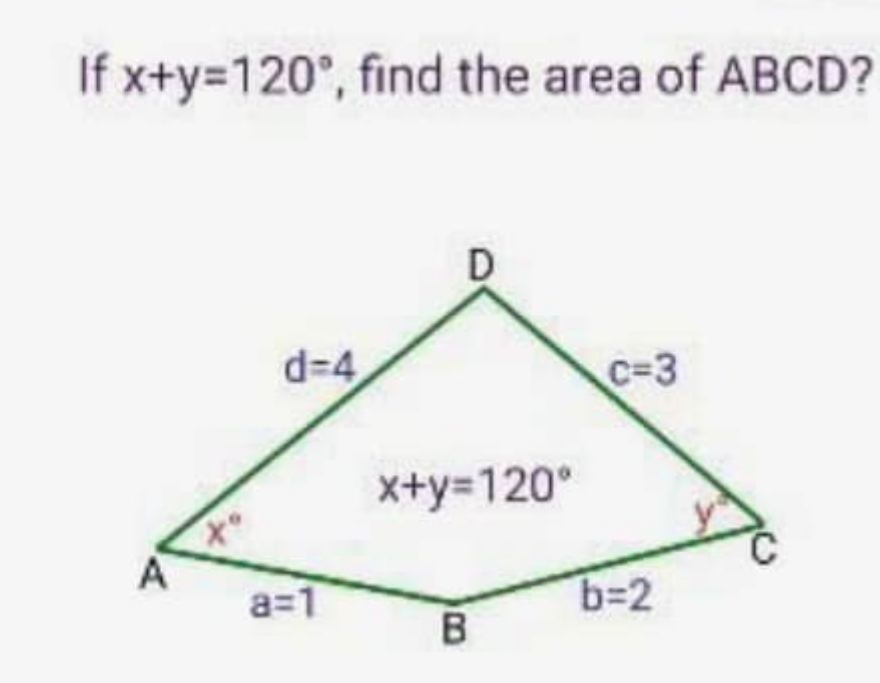
Question Number 211340 by Tawa11 last updated on 06/Sep/24

Commented by Frix last updated on 06/Sep/24

Question 211294

$$\mathrm{Question}\:\mathrm{211294} \\ $$

Answered by mr W last updated on 06/Sep/24

s=((a+b+c+d)/2)=((1+2+3+4)/2)=5 [ABCD]=(√((s−a)(s−b)(s−c)(s−d)−abcd cos^2 (((x+y)/2)))) =(√(4×3×2×1−1×2×3×4 cos^2 60°)) =(√(24×(1−(1/4))))=3(√2) ✓

$${s}=\frac{{a}+{b}+{c}+{d}}{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}}{\mathrm{2}}=\mathrm{5} \\ $$$$\left[{ABCD}\right]=\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)−{abcd}\:\mathrm{cos}^{\mathrm{2}} \:\left(\frac{{x}+{y}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=\sqrt{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}−\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{60}°} \\ $$$$\:\:\:\:=\sqrt{\mathrm{24}×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)}=\mathrm{3}\sqrt{\mathrm{2}}\:\checkmark \\ $$

Commented by Tawa11 last updated on 06/Sep/24

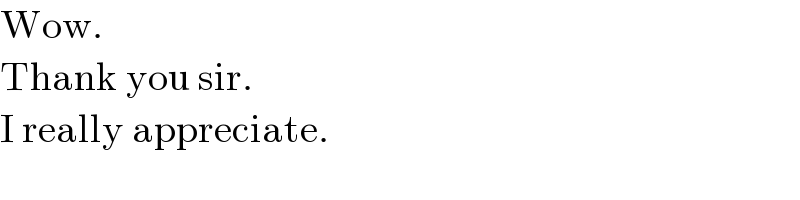
Wow. Thank you sir. I really appreciate.

$$\mathrm{Wow}. \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 06/Sep/24

Commented by mr W last updated on 06/Sep/24

Commented by mr W last updated on 06/Sep/24

see also Q30233

$${see}\:{also}\:{Q}\mathrm{30233} \\ $$

Answered by mahdipoor last updated on 06/Sep/24

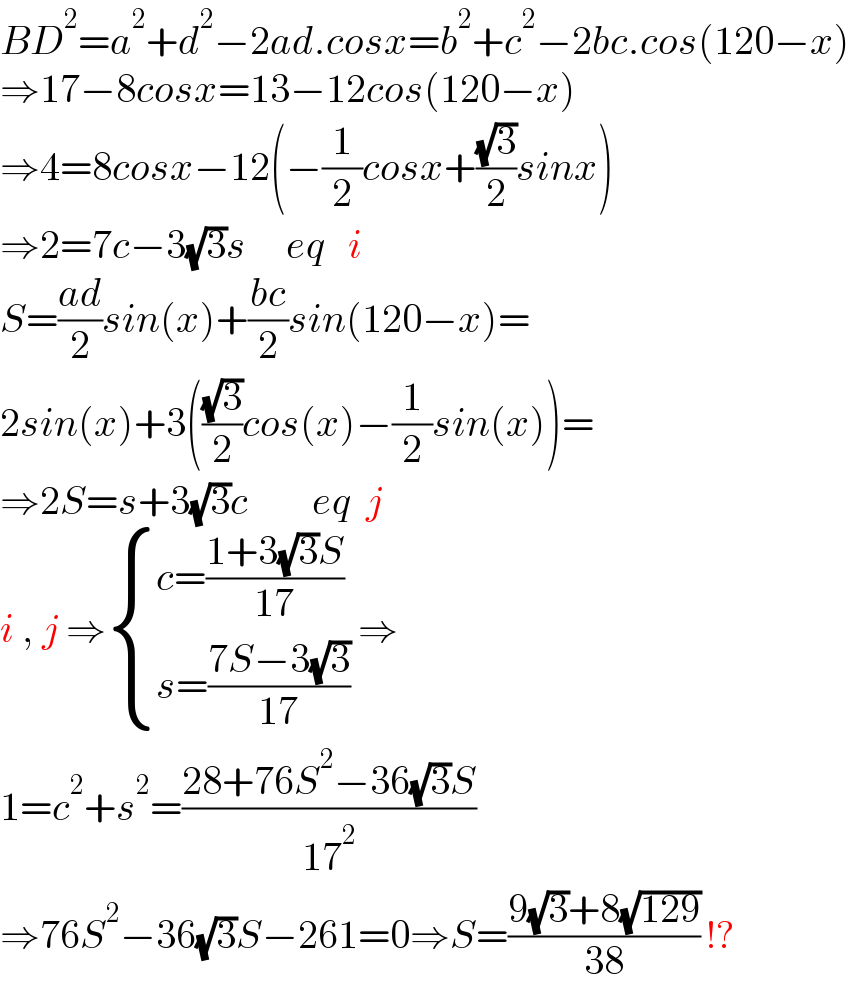
BD^2 =a^2 +d^2 −2ad.cosx=b^2 +c^2 −2bc.cos(120−x) ⇒17−8cosx=13−12cos(120−x) ⇒4=8cosx−12(−(1/2)cosx+((√3)/2)sinx) ⇒2=7c−3(√3)s eq i S=((ad)/2)sin(x)+((bc)/2)sin(120−x)= 2sin(x)+3(((√3)/2)cos(x)−(1/2)sin(x))= ⇒2S=s+3(√3)c eq j i , j ⇒ { ((c=((1+3(√3)S)/(17)))),((s=((7S−3(√3))/(17)))) :} ⇒ 1=c^2 +s^2 =((28+76S^2 −36(√3)S)/(17^2 )) ⇒76S^2 −36(√3)S−261=0⇒S=((9(√3)+8(√(129)))/(38)) !?

$${BD}^{\mathrm{2}} ={a}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ad}.{cosx}={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}.{cos}\left(\mathrm{120}−{x}\right) \\ $$$$\Rightarrow\mathrm{17}−\mathrm{8}{cosx}=\mathrm{13}−\mathrm{12}{cos}\left(\mathrm{120}−{x}\right) \\ $$$$\Rightarrow\mathrm{4}=\mathrm{8}{cosx}−\mathrm{12}\left(−\frac{\mathrm{1}}{\mathrm{2}}{cosx}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sinx}\right) \\ $$$$\Rightarrow\mathrm{2}=\mathrm{7}{c}−\mathrm{3}\sqrt{\mathrm{3}}{s}\:\:\:\:\:{eq}\:\:\:{i} \\ $$$${S}=\frac{{ad}}{\mathrm{2}}{sin}\left({x}\right)+\frac{{bc}}{\mathrm{2}}{sin}\left(\mathrm{120}−{x}\right)= \\ $$$$\mathrm{2}{sin}\left({x}\right)+\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left({x}\right)\right)= \\ $$$$\Rightarrow\mathrm{2}{S}={s}+\mathrm{3}\sqrt{\mathrm{3}}{c}\:\:\:\:\:\:\:\:{eq}\:\:{j} \\ $$$${i}\:,\:{j}\:\Rightarrow\begin{cases}{{c}=\frac{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{3}}{S}}{\mathrm{17}}}\\{{s}=\frac{\mathrm{7}{S}−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{17}}}\end{cases}\:\Rightarrow\: \\ $$$$\mathrm{1}={c}^{\mathrm{2}} +{s}^{\mathrm{2}} =\frac{\mathrm{28}+\mathrm{76}{S}^{\mathrm{2}} −\mathrm{36}\sqrt{\mathrm{3}}{S}}{\mathrm{17}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{76}{S}^{\mathrm{2}} −\mathrm{36}\sqrt{\mathrm{3}}{S}−\mathrm{261}=\mathrm{0}\Rightarrow{S}=\frac{\mathrm{9}\sqrt{\mathrm{3}}+\mathrm{8}\sqrt{\mathrm{129}}}{\mathrm{38}}\:!? \\ $$

Commented by Frix last updated on 06/Sep/24

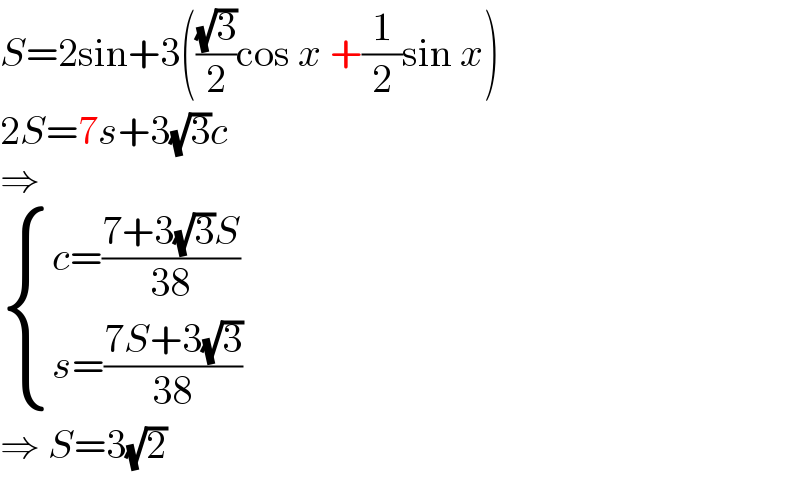
S=2sin+3(((√3)/2)cos x +(1/2)sin x) 2S=7s+3(√3)c ⇒ { ((c=((7+3(√3)S)/(38)))),((s=((7S+3(√3))/(38)))) :} ⇒ S=3(√2)

$${S}=\mathrm{2sin}+\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}\right) \\ $$$$\mathrm{2}{S}=\mathrm{7}{s}+\mathrm{3}\sqrt{\mathrm{3}}{c} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{c}=\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{3}}{S}}{\mathrm{38}}}\\{{s}=\frac{\mathrm{7}{S}+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{38}}}\end{cases} \\ $$$$\Rightarrow\:{S}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com