Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 211277 by mr W last updated on 04/Sep/24

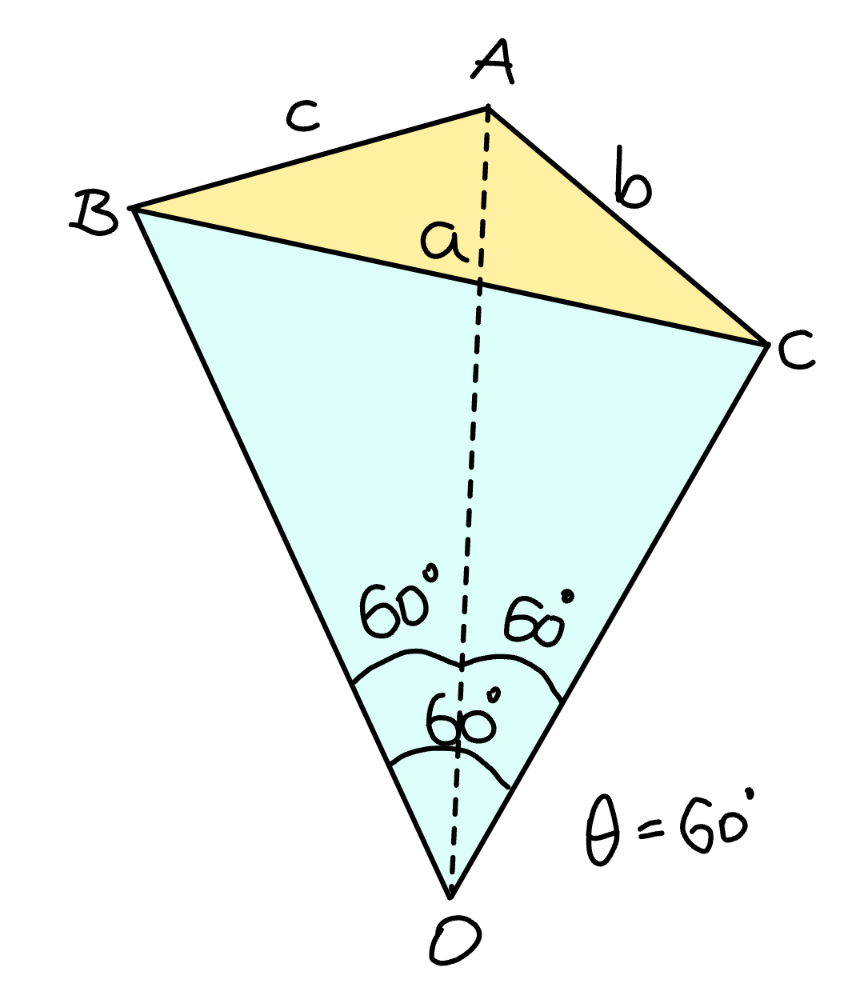
Commented by mr W last updated on 04/Sep/24

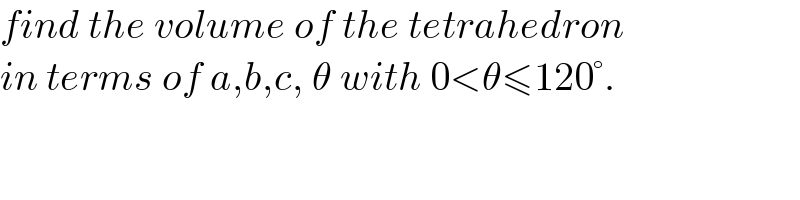
find the volume of the tetrahedron in terms of a,b,c, θ with 0<θ≤120°.

$${find}\:{the}\:{volume}\:{of}\:{the}\:{tetrahedron} \\ $$$${in}\:{terms}\:{of}\:{a},{b},{c},\:\theta\:{with}\:\mathrm{0}<\theta\leqslant\mathrm{120}°. \\ $$

Commented by mr W last updated on 07/Sep/24

for θ≠120° i don′t think point O is the fermat point in bottom view. if you think it is, please prove that and show your working. i don′t have the solution.

$${for}\:\theta\neq\mathrm{120}°\:{i}\:{don}'{t}\:{think}\:{point}\:{O}\:{is} \\ $$$${the}\:{fermat}\:{point}\:{in}\:{bottom}\:{view}.\: \\ $$$${if}\:{you}\:{think}\:{it}\:{is},\:{please}\:{prove}\:{that} \\ $$$${and}\:{show}\:{your}\:{working}. \\ $$$${i}\:{don}'{t}\:{have}\:{the}\:{solution}. \\ $$

Commented by Ghisom last updated on 21/Jun/25

I don′t think we can reach an explicit general solution. I tried for a=3, b=4, c=5, α=60°. we get 2 solutions, but we have to solve a quartic with no “nice” solution. I′m interested in the ellipse determined by A, B, C and the cone wrapping the tetrahedron. will post my result tomorrow, it′s 23:40 where I live...

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{reach}\:\mathrm{an}\:\mathrm{explicit} \\ $$$$\mathrm{general}\:\mathrm{solution}.\:\mathrm{I}\:\mathrm{tried}\:\mathrm{for}\:{a}=\mathrm{3},\:{b}=\mathrm{4}, \\ $$$${c}=\mathrm{5},\:\alpha=\mathrm{60}°.\:\mathrm{we}\:\mathrm{get}\:\mathrm{2}\:\mathrm{solutions},\:\mathrm{but}\:\mathrm{we} \\ $$$$\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{a}\:\mathrm{quartic}\:\mathrm{with}\:\mathrm{no}\:``\mathrm{nice}'' \\ $$$$\mathrm{solution}. \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{interested}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{determined} \\ $$$$\mathrm{by}\:{A},\:{B},\:{C}\:\mathrm{and}\:\mathrm{the}\:\mathrm{cone}\:\mathrm{wrapping}\:\mathrm{the} \\ $$$$\mathrm{tetrahedron}.\:\mathrm{will}\:\mathrm{post}\:\mathrm{my}\:\mathrm{result}\:\mathrm{tomorrow}, \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{23}:\mathrm{40}\:\mathrm{where}\:\mathrm{I}\:\mathrm{live}... \\ $$

Commented by Ghisom last updated on 22/Jun/25

...it′s even more complicated. the conic is a byperbola in this case ⇒ we must determine either • for a given triangle which angles α are leading to a closed tetrahedron or • for a given α which triangles are possible

$$...\mathrm{it}'\mathrm{s}\:\mathrm{even}\:\mathrm{more}\:\mathrm{complicated}. \\ $$$$\mathrm{the}\:\mathrm{conic}\:\mathrm{is}\:\mathrm{a}\:\mathrm{byperbola}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$$\Rightarrow \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{determine}\:\mathrm{either} \\ $$$$\bullet\:\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:\mathrm{triangle}\:\mathrm{which}\:\mathrm{angles}\:\alpha\:\mathrm{are} \\ $$$$\mathrm{leading}\:\mathrm{to}\:\mathrm{a}\:\mathrm{closed}\:\mathrm{tetrahedron}\:\mathrm{or} \\ $$$$\bullet\:\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:\alpha\:\mathrm{which}\:\mathrm{triangles}\:\mathrm{are}\:\mathrm{possible} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com