Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 211235 by behi834171 last updated on 01/Sep/24

Commented by behi834171 last updated on 01/Sep/24

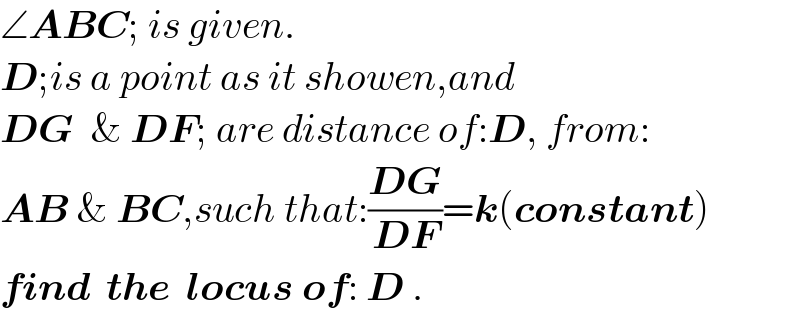
∠ABC; is given. D;is a point as it showen,and DG & DF; are distance of:D, from: AB & BC,such that:((DG)/(DF))=k(constant) find the locus of: D .

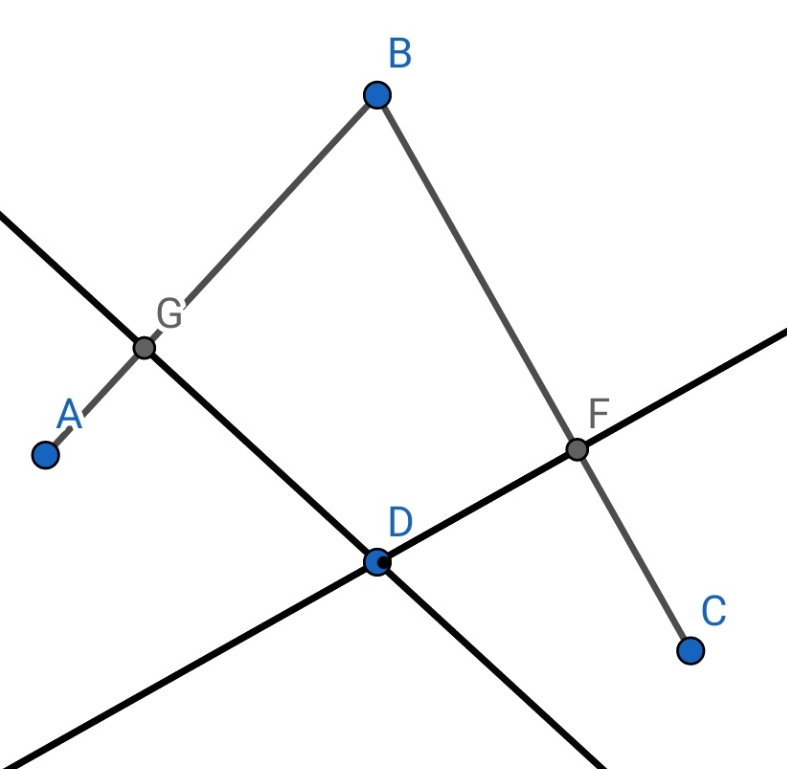
$$\angle\boldsymbol{{ABC}};\:{is}\:{given}. \\ $$$$\boldsymbol{{D}};{is}\:{a}\:{point}\:{as}\:{it}\:{showen},{and} \\ $$$$\boldsymbol{{DG}}\:\:\&\:\boldsymbol{{DF}};\:{are}\:{distance}\:{of}:\boldsymbol{{D}},\:{from}: \\ $$$$\boldsymbol{{AB}}\:\&\:\boldsymbol{{BC}},{such}\:{that}:\frac{\boldsymbol{{DG}}}{\boldsymbol{{DF}}}=\boldsymbol{{k}}\left(\boldsymbol{{constant}}\right) \\ $$$$\boldsymbol{{find}}\:\:\boldsymbol{{the}}\:\:\boldsymbol{{locus}}\:\boldsymbol{{of}}:\:\boldsymbol{{D}}\:. \\ $$

Answered by A5T last updated on 01/Sep/24

Commented by A5T last updated on 01/Sep/24

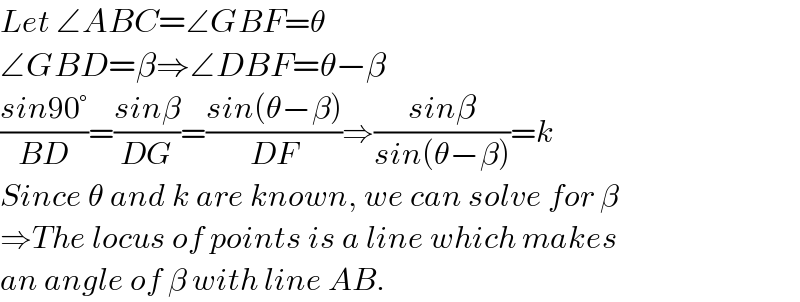
Let ∠ABC=∠GBF=θ ∠GBD=β⇒∠DBF=θ−β ((sin90°)/(BD))=((sinβ)/(DG))=((sin(θ−β))/(DF))⇒((sinβ)/(sin(θ−β)))=k Since θ and k are known, we can solve for β ⇒The locus of points is a line which makes an angle of β with line AB.

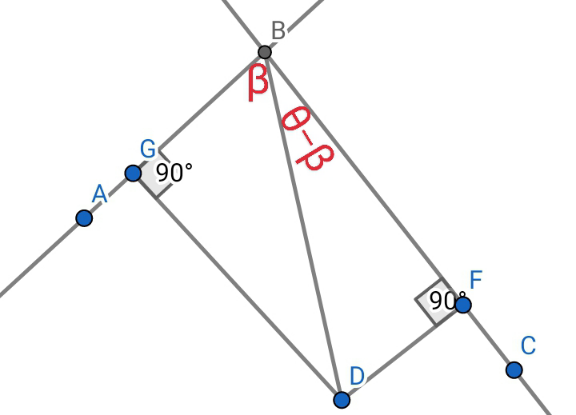
$${Let}\:\angle{ABC}=\angle{GBF}=\theta \\ $$$$\angle{GBD}=\beta\Rightarrow\angle{DBF}=\theta−\beta \\ $$$$\frac{{sin}\mathrm{90}°}{{BD}}=\frac{{sin}\beta}{{DG}}=\frac{{sin}\left(\theta−\beta\right)}{{DF}}\Rightarrow\frac{{sin}\beta}{{sin}\left(\theta−\beta\right)}={k} \\ $$$${Since}\:\theta\:{and}\:{k}\:{are}\:{known},\:{we}\:{can}\:{solve}\:{for}\:\beta \\ $$$$\Rightarrow{The}\:{locus}\:{of}\:{points}\:{is}\:{a}\:{line}\:{which}\:{makes} \\ $$$${an}\:{angle}\:{of}\:\beta\:{with}\:{line}\:{AB}.\: \\ $$

Commented by behi834171 last updated on 01/Sep/24

Thank you sir AST. yes.the locus is a line crosses at B point.

$${Thank}\:{you}\:{sir}\:{AST}. \\ $$$${yes}.{the}\:{locus}\:{is}\:{a}\:{line}\:{crosses}\:{at}\:{B}\:{point}. \\ $$

Answered by mr W last updated on 01/Sep/24

Commented by mr W last updated on 01/Sep/24

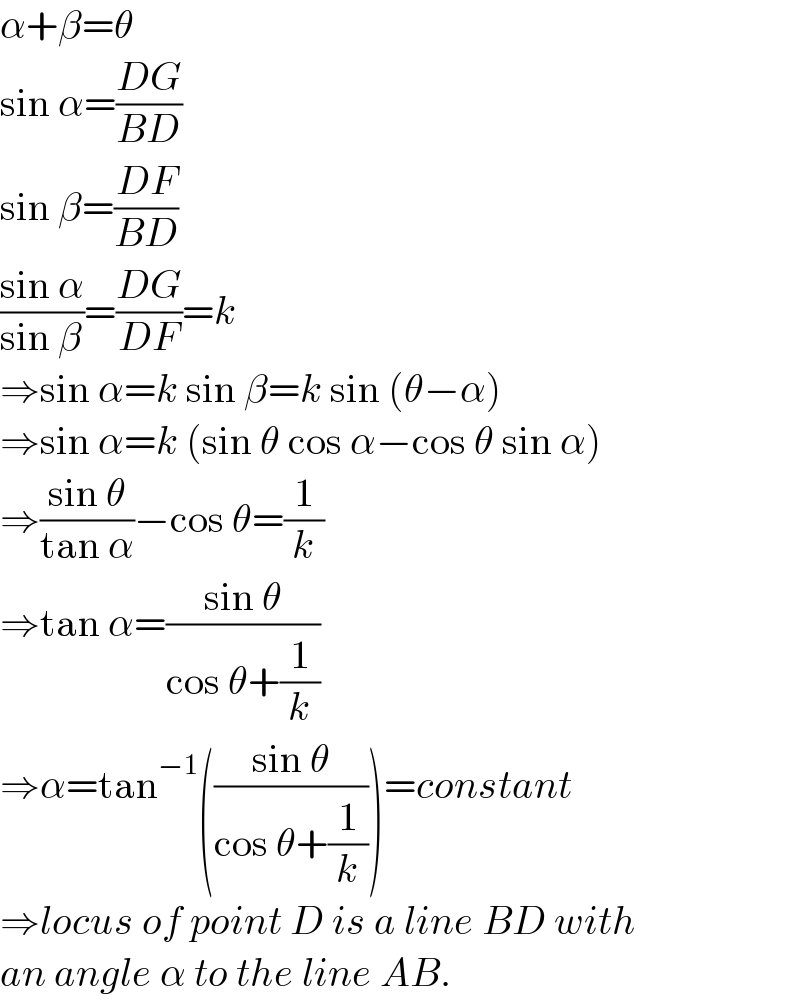
α+β=θ sin α=((DG)/(BD)) sin β=((DF)/(BD)) ((sin α)/(sin β))=((DG)/(DF))=k ⇒sin α=k sin β=k sin (θ−α) ⇒sin α=k (sin θ cos α−cos θ sin α) ⇒((sin θ)/(tan α))−cos θ=(1/k) ⇒tan α=((sin θ)/(cos θ+(1/k))) ⇒α=tan^(−1) (((sin θ)/(cos θ+(1/k))))=constant ⇒locus of point D is a line BD with an angle α to the line AB.

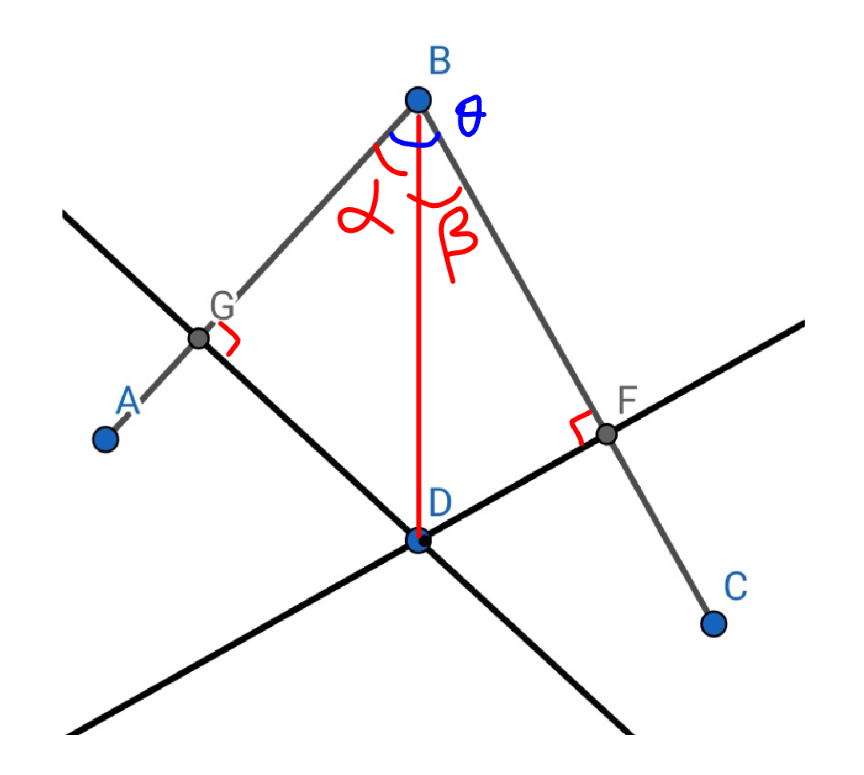
$$\alpha+\beta=\theta \\ $$$$\mathrm{sin}\:\alpha=\frac{{DG}}{{BD}} \\ $$$$\mathrm{sin}\:\beta=\frac{{DF}}{{BD}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\beta}=\frac{{DG}}{{DF}}={k}\: \\ $$$$\Rightarrow\mathrm{sin}\:\alpha={k}\:\mathrm{sin}\:\beta={k}\:\mathrm{sin}\:\left(\theta−\alpha\right) \\ $$$$\Rightarrow\mathrm{sin}\:\alpha={k}\:\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha\right) \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha}−\mathrm{cos}\:\theta=\frac{\mathrm{1}}{{k}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta+\frac{\mathrm{1}}{{k}}} \\ $$$$\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta+\frac{\mathrm{1}}{{k}}}\right)={constant} \\ $$$$\Rightarrow{locus}\:{of}\:{point}\:{D}\:{is}\:{a}\:{line}\:{BD}\:{with} \\ $$$${an}\:{angle}\:\alpha\:{to}\:{the}\:{line}\:{AB}. \\ $$

Commented by behi834171 last updated on 01/Sep/24

Thank you so much dear master. If we have just two intersecting lines,inested of given angle:ABC; is the locus unique?

$${Thank}\:{you}\:{so}\:{much}\:{dear}\:{master}. \\ $$$$ \\ $$If we have just two intersecting lines,inested of given angle:ABC; is the locus unique?

Commented by mr W last updated on 01/Sep/24

in this case the point can be every where except (0,0).

$${in}\:{this}\:{case}\:{the}\:{point}\:{can}\:{be}\:{every} \\ $$$${where}\:{except}\:\left(\mathrm{0},\mathrm{0}\right). \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com