Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 211129 by depressiveshrek last updated on 29/Aug/24

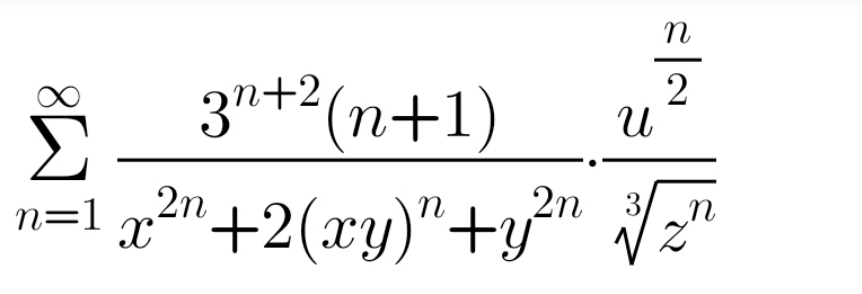
Commented by depressiveshrek last updated on 29/Aug/24

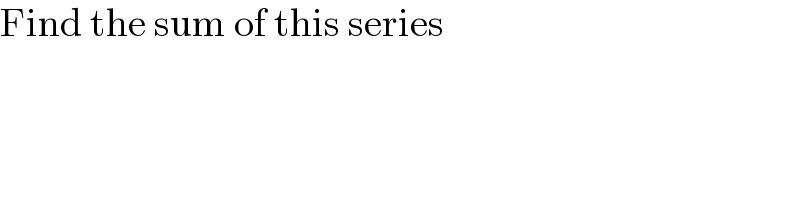
Find the sum of this series

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{this}\:\mathrm{series} \\ $$

Answered by mr W last updated on 29/Aug/24

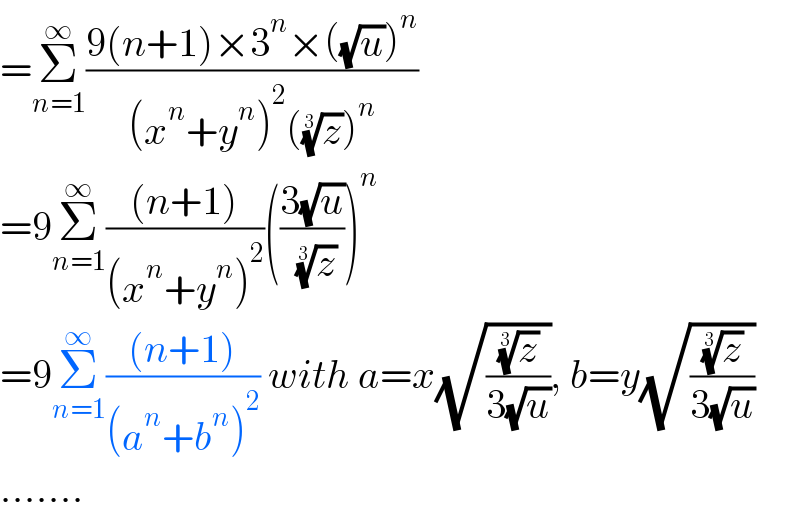
=Σ_(n=1) ^∞ ((9(n+1)×3^n ×((√u))^n )/((x^n +y^n )^2 ((z)^(1/3) )^n )) =9Σ_(n=1) ^∞ (((n+1))/((x^n +y^n )^2 ))(((3(√u))/( (z)^(1/3) )))^n =9Σ_(n=1) ^∞ (((n+1))/((a^n +b^n )^2 )) with a=x(√((z)^(1/3) /(3(√u)))), b=y(√((z)^(1/3) /(3(√u)))) .......

$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{9}\left({n}+\mathrm{1}\right)×\mathrm{3}^{{n}} ×\left(\sqrt{{u}}\right)^{{n}} }{\left({x}^{{n}} +{y}^{{n}} \right)^{\mathrm{2}} \left(\sqrt[{\mathrm{3}}]{{z}}\right)^{{n}} } \\ $$$$=\mathrm{9}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)}{\left({x}^{{n}} +{y}^{{n}} \right)^{\mathrm{2}} }\left(\frac{\mathrm{3}\sqrt{{u}}}{\:\sqrt[{\mathrm{3}}]{{z}}}\right)^{{n}} \\ $$$$=\mathrm{9}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)}{\left({a}^{{n}} +{b}^{{n}} \right)^{\mathrm{2}} }\:{with}\:{a}={x}\sqrt{\frac{\sqrt[{\mathrm{3}}]{{z}}}{\mathrm{3}\sqrt{{u}}}},\:{b}={y}\sqrt{\frac{\sqrt[{\mathrm{3}}]{{z}}}{\mathrm{3}\sqrt{{u}}}} \\ $$$$....... \\ $$

Commented by mr W last updated on 29/Aug/24

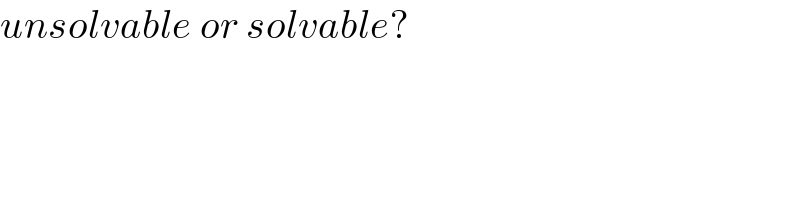
unsolvable or solvable?

$${unsolvable}\:{or}\:{solvable}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com