
Question Number 211105 by peter frank last updated on 28/Aug/24

Answered by mm1342 last updated on 28/Aug/24
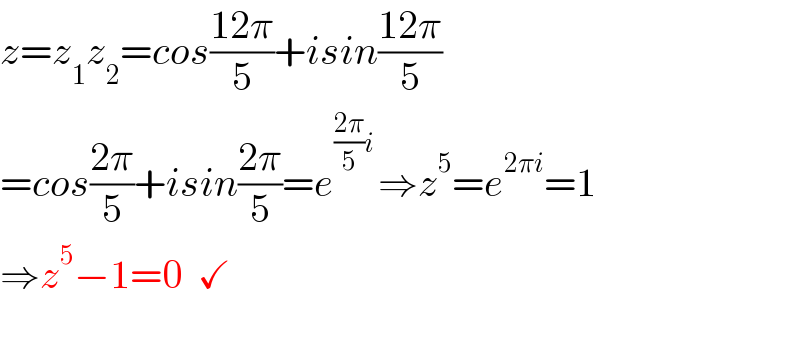
$${z}={z}_{\mathrm{1}} {z}_{\mathrm{2}} ={cos}\frac{\mathrm{12}\pi}{\mathrm{5}}+{isin}\frac{\mathrm{12}\pi}{\mathrm{5}} \\ $$$$={cos}\frac{\mathrm{2}\pi}{\mathrm{5}}+{isin}\frac{\mathrm{2}\pi}{\mathrm{5}}={e}^{\frac{\mathrm{2}\pi}{\mathrm{5}}{i}\:} \Rightarrow{z}^{\mathrm{5}} ={e}^{\mathrm{2}\pi{i}} =\mathrm{1} \\ $$$$\Rightarrow{z}^{\mathrm{5}} −\mathrm{1}=\mathrm{0}\:\:\checkmark \\ $$$$ \\ $$
Commented by peter frank last updated on 28/Aug/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Frix last updated on 28/Aug/24
![z^5 =e^(2πni) ; n∈Z z_n =e^(((2πn)/5)i) ⇔ Z_5 ={z_n =e^(((2πn)/5)i) ∣n∈Z} [Further we notice e^(((2πn)/5)i) =e^(((2(n+5k)π)/5)i) ; k∈Z] z_m z_n =e^(((2πm)/5)i) e^(((2πn)/5)i) =e^(((2π(m+n))/5)i) m, n ∈Z ⇒ z_m , z_n ∈Z_5 m+n∈Z ⇒ z_(m+n) ∈Z_5 z_1 =e^(((4π)/5)i) =z_2 ∈Z_5 [4=2n ⇔ n=2] z_2 =e^(((8π)/5)i) =z_4 ∈Z_5 [8=2n ⇔ n=4] z_1 z_2 =e^(((12π)/5)i) =z_6 ∈Z_5 [12=2n ⇔ n=6] [12=2(n+5k) ⇔ n=1∧k=1]](Q211112.png)
$${z}^{\mathrm{5}} =\mathrm{e}^{\mathrm{2}\pi{n}\mathrm{i}} ;\:{n}\in\mathbb{Z} \\ $$$${z}_{{n}} =\mathrm{e}^{\frac{\mathrm{2}\pi{n}}{\mathrm{5}}\mathrm{i}} \\ $$$$\Leftrightarrow \\ $$$${Z}_{\mathrm{5}} =\left\{{z}_{{n}} =\mathrm{e}^{\frac{\mathrm{2}\pi{n}}{\mathrm{5}}\mathrm{i}} \mid{n}\in\mathbb{Z}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{Further}\:\mathrm{we}\:\mathrm{notice}\:\mathrm{e}^{\frac{\mathrm{2}\pi{n}}{\mathrm{5}}\mathrm{i}} =\mathrm{e}^{\frac{\mathrm{2}\left({n}+\mathrm{5}{k}\right)\pi}{\mathrm{5}}\mathrm{i}} ;\:{k}\in\mathbb{Z}\right] \\ $$$$ \\ $$$${z}_{{m}} {z}_{{n}} =\mathrm{e}^{\frac{\mathrm{2}\pi{m}}{\mathrm{5}}\mathrm{i}} \mathrm{e}^{\frac{\mathrm{2}\pi{n}}{\mathrm{5}}\mathrm{i}} =\mathrm{e}^{\frac{\mathrm{2}\pi\left({m}+{n}\right)}{\mathrm{5}}\mathrm{i}} \\ $$$${m},\:{n}\:\in\mathbb{Z}\:\Rightarrow\:{z}_{{m}} ,\:{z}_{{n}} \:\in{Z}_{\mathrm{5}} \\ $$$${m}+{n}\in\mathbb{Z}\:\Rightarrow\:{z}_{{m}+{n}} \in{Z}_{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{z}_{\mathrm{1}} =\mathrm{e}^{\frac{\mathrm{4}\pi}{\mathrm{5}}\mathrm{i}} ={z}_{\mathrm{2}} \in{Z}_{\mathrm{5}} \:\:\:\:\:\left[\mathrm{4}=\mathrm{2}{n}\:\Leftrightarrow\:{n}=\mathrm{2}\right] \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{e}^{\frac{\mathrm{8}\pi}{\mathrm{5}}\mathrm{i}} ={z}_{\mathrm{4}} \in{Z}_{\mathrm{5}} \:\:\:\:\:\left[\mathrm{8}=\mathrm{2}{n}\:\Leftrightarrow\:{n}=\mathrm{4}\right] \\ $$$$\mathrm{z}_{\mathrm{1}} \mathrm{z}_{\mathrm{2}} =\mathrm{e}^{\frac{\mathrm{12}\pi}{\mathrm{5}}\mathrm{i}} ={z}_{\mathrm{6}} \in{Z}_{\mathrm{5}} \:\:\:\:\:\left[\mathrm{12}=\mathrm{2}{n}\:\Leftrightarrow\:{n}=\mathrm{6}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{12}=\mathrm{2}\left({n}+\mathrm{5}{k}\right)\:\Leftrightarrow\:{n}=\mathrm{1}\wedge{k}=\mathrm{1}\right] \\ $$
Commented by peter frank last updated on 28/Aug/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
