
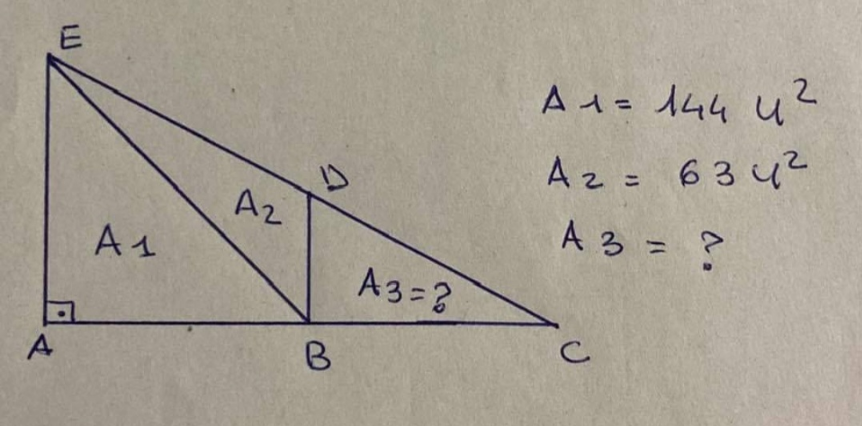
Question Number 211079 by Ari last updated on 27/Aug/24
Answered by A5T last updated on 27/Aug/24
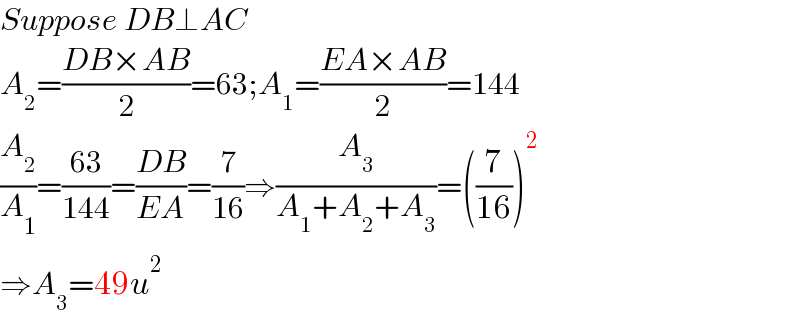
$${Suppose}\:{DB}\bot{AC} \\ $$$${A}_{\mathrm{2}} =\frac{{DB}×{AB}}{\mathrm{2}}=\mathrm{63};{A}_{\mathrm{1}} =\frac{{EA}×{AB}}{\mathrm{2}}=\mathrm{144} \\ $$$$\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }=\frac{\mathrm{63}}{\mathrm{144}}=\frac{{DB}}{{EA}}=\frac{\mathrm{7}}{\mathrm{16}}\Rightarrow\frac{{A}_{\mathrm{3}} }{{A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} }=\left(\frac{\mathrm{7}}{\mathrm{16}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{A}_{\mathrm{3}} =\mathrm{49}{u}^{\mathrm{2}} \\ $$
Commented by Ari last updated on 27/Aug/24

$${but}\:{DB}\:{is}\:{not}\:{given}\:{perpendicular}\:{to}\:{AC} \\ $$$$ \\ $$
Commented by A5T last updated on 27/Aug/24

$${Then}\:{it}\:{cannot}\:{be}\:{unique}\:{or}\:{it}\:{won}'{t}\:{be}\: \\ $$$${dependent}\:{on}\:{it}\:{being}\:{perpendicular} \\ $$
Commented by Ari last updated on 27/Aug/24
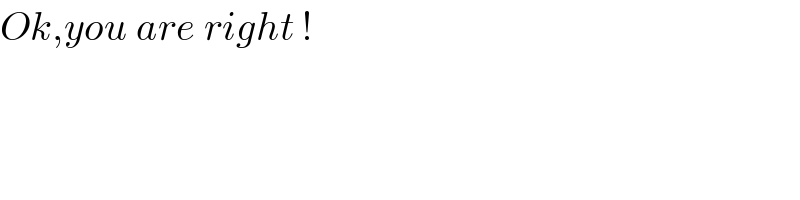
$${Ok},{you}\:{are}\:{right}\:! \\ $$
Commented by mm1342 last updated on 27/Aug/24
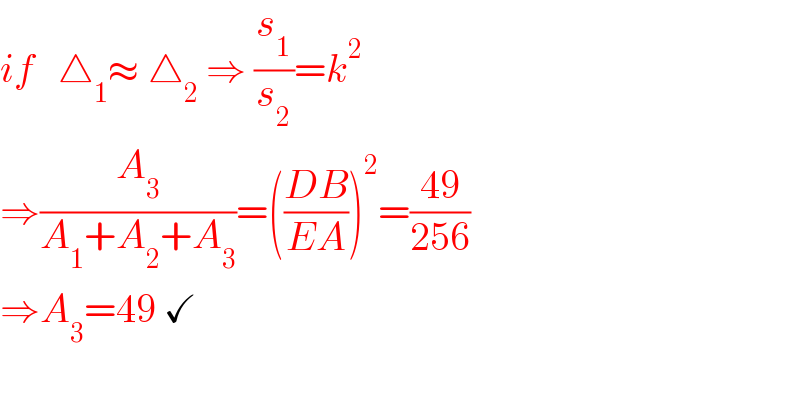
$${if}\:\:\:\bigtriangleup_{\mathrm{1}} \approx\:\bigtriangleup_{\mathrm{2}} \:\Rightarrow\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }={k}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{A}_{\mathrm{3}} }{{A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} }=\left(\frac{{DB}}{{EA}}\right)^{\mathrm{2}} =\frac{\mathrm{49}}{\mathrm{256}} \\ $$$$\Rightarrow{A}_{\mathrm{3}} =\mathrm{49}\:\checkmark \\ $$$$ \\ $$
