Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 211029 by BaliramKumar last updated on 26/Aug/24

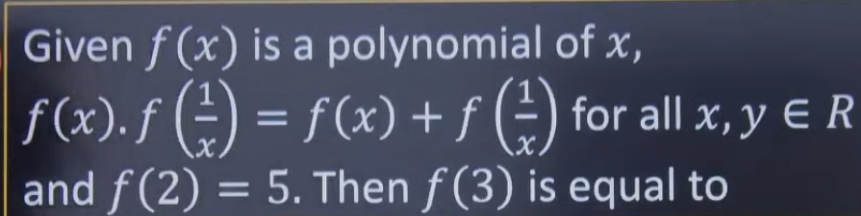
Answered by Ar Brandon last updated on 26/Aug/24

f(2)=5 therefore f(x) must be a non-zero polynomial. Let f(x)=a_0 +a_1 x+a_2 x^2 +∙∙∙+a_n x^n , a_n ≠0 Suppose f(x)+f((1/x))=f(x)f((1/x)) for all x≠0 Then Σ_(r=0) ^n a_r x^r +Σ_(r=1) ^n (a_r /x^r )=(Σ_(r=0) ^n a_r x^r )(Σ_(r=1) ^n (a_r /x^r )) Multiplying through by x^n , Σ_(r=0) ^n a_r x^(n+r) +Σ_(r=0) ^n a_r x^(n−r) =(Σ_(r=0) ^n a_r x^r )(Σ_(r=0) ^n a_r x^(n−r) ) That is, (a_0 x^n +a_1 x^(n+1) +∙∙∙a_n x^(2n) )+(a_0 x^n +a_1 x^(n−1) +∙∙∙+a_(n−1) x+a_n ) =(a_0 +a_1 x+∙∙∙a_n x^n )(a_0 x^n +a_1 x^(n−1) +∙∙∙+a_(n−1) x+a_n ) Equating the corresponding coefficients of powers of x, we have a_n =a_0 a_n , a_(n−1) =a_0 a_(n−1) +a_1 a_n a_(n−2) =a_2 a_n +a_1 a_(n−1) +a_(n−2) a_0 2a_0 =a_0 ^2 +a_n ^2 a_n =a_0 a_n ⇒a_0 =1 (since a_n ≠0) a_(n−1) =a_0 a_(n−1) +a_1 a_n ⇒a_1 a_n =0⇒a_1 =0 a_(n−2) =a_2 a_n +a_1 a_(n−1) +a_(n−2) a_0 ⇒a_(n−2) =a_2 a_n +a_(n−2) ⇒a_2 =0 Continuing this process, we get a_(n−1) =0 and 2=1+a_n ^2 . Hence a_n =±1. Therefore f(x)=1±x^n But f(2)=5 hence 5=1±2^n Therefore f(x) cannot be 1−x^n . Thus, f(x)=1+x^n and 5=1+2^n ⇒ n=2. So f(x)=1+x^2 and determinant (((f(3)=10))).

$${f}\left(\mathrm{2}\right)=\mathrm{5}\:\mathrm{therefore}\:{f}\left({x}\right)\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{non}-\mathrm{zero}\:\mathrm{polynomial}. \\ $$$$\mathrm{Let}\:{f}\left({x}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +\centerdot\centerdot\centerdot+{a}_{{n}} {x}^{{n}} ,\:{a}_{{n}} \neq\mathrm{0} \\ $$$$\mathrm{Suppose}\:{f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)={f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)\:\mathrm{for}\:\mathrm{all}\:{x}\neq\mathrm{0} \\ $$$$\mathrm{Then}\:\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{\mathrm{r}} +\underset{\mathrm{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{a}_{\mathrm{r}} }{{x}^{\mathrm{r}} }=\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{\mathrm{r}} \right)\left(\underset{\mathrm{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{a}_{\mathrm{r}} }{{x}^{\mathrm{r}} }\right) \\ $$$$\mathrm{Multiplying}\:\mathrm{through}\:\mathrm{by}\:{x}^{{n}} , \\ $$$$\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{{n}+\mathrm{r}} +\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{{n}−\mathrm{r}} =\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{\mathrm{r}} \right)\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{\mathrm{r}} {x}^{{n}−\mathrm{r}} \right) \\ $$$$\mathrm{That}\:\mathrm{is}, \\ $$$$\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}+\mathrm{1}} +\centerdot\centerdot\centerdot{a}_{{n}} {x}^{\mathrm{2}{n}} \right)+\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +\centerdot\centerdot\centerdot+{a}_{{n}−\mathrm{1}} {x}+{a}_{{n}} \right) \\ $$$$\:\:\:\:\:\:=\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+\centerdot\centerdot\centerdot{a}_{{n}} {x}^{{n}} \right)\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +\centerdot\centerdot\centerdot+{a}_{{n}−\mathrm{1}} {x}+{a}_{{n}} \right) \\ $$$$\mathrm{Equating}\:\mathrm{the}\:\mathrm{corresponding}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{powers}\:\mathrm{of}\:{x}, \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\:\:\:\:\:\:\:\:\:{a}_{{n}} ={a}_{\mathrm{0}} {a}_{{n}} ,\:{a}_{{n}−\mathrm{1}} ={a}_{\mathrm{0}} {a}_{{n}−\mathrm{1}} +{a}_{\mathrm{1}} {a}_{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:{a}_{{n}−\mathrm{2}} ={a}_{\mathrm{2}} {a}_{{n}} +{a}_{\mathrm{1}} {a}_{{n}−\mathrm{1}} +{a}_{{n}−\mathrm{2}} {a}_{\mathrm{0}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}{a}_{\mathrm{0}} ={a}_{\mathrm{0}} ^{\mathrm{2}} +{a}_{{n}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}_{{n}} ={a}_{\mathrm{0}} {a}_{{n}} \Rightarrow{a}_{\mathrm{0}} =\mathrm{1}\:\left(\mathrm{since}\:{a}_{{n}} \neq\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}_{{n}−\mathrm{1}} ={a}_{\mathrm{0}} {a}_{{n}−\mathrm{1}} +{a}_{\mathrm{1}} {a}_{{n}} \Rightarrow{a}_{\mathrm{1}} {a}_{{n}} =\mathrm{0}\Rightarrow{a}_{\mathrm{1}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}_{{n}−\mathrm{2}} ={a}_{\mathrm{2}} {a}_{{n}} +{a}_{\mathrm{1}} {a}_{{n}−\mathrm{1}} +{a}_{{n}−\mathrm{2}} {a}_{\mathrm{0}} \Rightarrow{a}_{{n}−\mathrm{2}} ={a}_{\mathrm{2}} {a}_{{n}} +{a}_{{n}−\mathrm{2}} \Rightarrow{a}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Continuing}\:\mathrm{this}\:\mathrm{process},\:\mathrm{we}\:\mathrm{get}\:{a}_{{n}−\mathrm{1}} =\mathrm{0}\:\mathrm{and}\:\mathrm{2}=\mathrm{1}+{a}_{{n}} ^{\mathrm{2}} . \\ $$$$\mathrm{Hence}\:{a}_{{n}} =\pm\mathrm{1}.\:\mathrm{Therefore} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left({x}\right)=\mathrm{1}\pm{x}^{{n}} \\ $$$$\mathrm{But}\:{f}\left(\mathrm{2}\right)=\mathrm{5}\:\mathrm{hence} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}=\mathrm{1}\pm\mathrm{2}^{\mathrm{n}} \\ $$$$\mathrm{Therefore}\:{f}\left({x}\right)\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{1}−{x}^{{n}} .\:\mathrm{Thus},\:{f}\left({x}\right)=\mathrm{1}+{x}^{{n}} \:\mathrm{and} \\ $$$$\mathrm{5}=\mathrm{1}+\mathrm{2}^{{n}} \:\Rightarrow\:{n}=\mathrm{2}.\:\mathrm{So}\:{f}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{2}} \:\mathrm{and}\:\begin{array}{|c|}{{f}\left(\mathrm{3}\right)=\mathrm{10}}\\\hline\end{array}. \\ $$

Commented by Frix last updated on 26/Aug/24

��

Commented by Ar Brandon last updated on 26/Aug/24

Greetings, Sir! it's been quite a long time��

Commented by BaliramKumar last updated on 27/Aug/24

Thanks sir

$${Thanks}\:{sir} \\ $$

Commented by Ar Brandon last updated on 27/Aug/24

You're welcome!

Answered by Frix last updated on 26/Aug/24

We know 3 things: (1) f(x)f((1/x))=f(x)+f((1/x)) for all x∈R (2) f(2)=5 ((1) ⇒ f((1/x))=((f(x))/(f(x)+1))) ∧ (2) ⇒ (3) f((1/2))=(5/4) ⇒ we can have 3 unknowns ⇒ we have a polynomial of degree 2 ⇒ f(x)=ax^2 +bx+c (2) 4a+2b+c=5 (3) (a/4)+(b/2)+c=(5/4) ⇒ b=−((5(a−1))/2)∧a=c Insert into (1) & transform c^2 −((2(x^2 −5x+1))/((x−2)(2x−1)))c−((5x)/((x−2)(2x−1)))=0 ⇒ c=1∨c=−((5x)/((x−2)(2x−1))) Since c is a constant which must be valid for all x∈R ⇒ c=1 ⇒ a=1∧b=0 ⇒ f(x)=x^2 +1 f(3)=10

$$\mathrm{We}\:\mathrm{know}\:\mathrm{3}\:\mathrm{things}: \\ $$$$\:\:\:\:\:\left(\mathrm{1}\right)\:{f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)={f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)\:\mathrm{for}\:\mathrm{all}\:{x}\in\mathbb{R} \\ $$$$\:\:\:\:\:\left(\mathrm{2}\right)\:{f}\left(\mathrm{2}\right)=\mathrm{5} \\ $$$$\left(\left(\mathrm{1}\right)\:\Rightarrow\:{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{{f}\left({x}\right)}{{f}\left({x}\right)+\mathrm{1}}\right)\:\wedge\:\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\:\:\:\:\:\left(\mathrm{3}\right)\:{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{have}\:\mathrm{3}\:\mathrm{unknowns}\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{a} \\ $$$$\mathrm{polynomial}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{2}\:\Rightarrow \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{4}{a}+\mathrm{2}{b}+{c}=\mathrm{5} \\ $$$$\left(\mathrm{3}\right)\:\frac{{a}}{\mathrm{4}}+\frac{{b}}{\mathrm{2}}+{c}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\Rightarrow\:{b}=−\frac{\mathrm{5}\left({a}−\mathrm{1}\right)}{\mathrm{2}}\wedge{a}={c} \\ $$$$ \\ $$$$\mathrm{Insert}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\&\:\mathrm{transform} \\ $$$${c}^{\mathrm{2}} −\frac{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{1}\right)}{\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)}{c}−\frac{\mathrm{5}{x}}{\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)}=\mathrm{0} \\ $$$$\Rightarrow\:{c}=\mathrm{1}\vee{c}=−\frac{\mathrm{5}{x}}{\left({x}−\mathrm{2}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)} \\ $$$$\mathrm{Since}\:{c}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{which}\:\mathrm{must}\:\mathrm{be}\:\mathrm{valid} \\ $$$$\mathrm{for}\:\mathrm{all}\:{x}\in\mathbb{R} \\ $$$$\Rightarrow\:{c}=\mathrm{1} \\ $$$$\Rightarrow\:{a}=\mathrm{1}\wedge{b}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{10} \\ $$

Commented by BaliramKumar last updated on 27/Aug/24

Thanks sir

$${Thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com