Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 211019 by peter frank last updated on 26/Aug/24

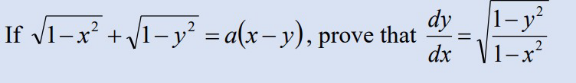
Answered by som(math1967) last updated on 26/Aug/24

let x=sinα y=sinβ cosα+cosβ=a(sinα−sinβ) ⇒((2cos((α+β)/2)cos((α−β)/2))/(2sin((α−β)/2)cos((α+β)/2)))=a ⇒cot((α−β)/2)=a ⇒(1/2)(α−β)=cot^(−1) a ⇒ sin^(−1) x−sin^(−1) y=2cot^(−1) a ⇒ (1/( (√(1−x^2 )))) −(1/( (√(1−y^2 ))))×(dy/dx)=0 ∴ (dy/dx)=(√((1−y^2 )/(1−x^2 )))

$$\:{let}\:{x}={sin}\alpha\:\:{y}={sin}\beta \\ $$$$\:{cos}\alpha+{cos}\beta={a}\left({sin}\alpha−{sin}\beta\right) \\ $$$$\Rightarrow\frac{\mathrm{2}{cos}\frac{\alpha+\beta}{\mathrm{2}}{cos}\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{2}{sin}\frac{\alpha−\beta}{\mathrm{2}}{cos}\frac{\alpha+\beta}{\mathrm{2}}}={a} \\ $$$$\Rightarrow{cot}\frac{\alpha−\beta}{\mathrm{2}}={a} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\alpha−\beta\right)=\mathrm{cot}^{−\mathrm{1}} {a} \\ $$$$\Rightarrow\:\mathrm{sin}^{−\mathrm{1}} {x}−\mathrm{sin}^{−\mathrm{1}} {y}=\mathrm{2cot}^{−\mathrm{1}} {a} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}×\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\:\therefore\:\frac{{dy}}{{dx}}=\sqrt{\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$

Commented by peter frank last updated on 27/Aug/24

thank you som

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{som} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com