
Question Number 211008 by mnjuly1970 last updated on 26/Aug/24
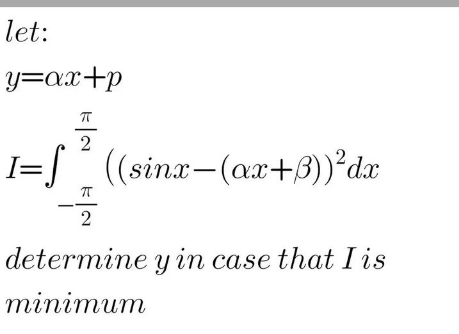
Commented by Frix last updated on 26/Aug/24

$${y}=\alpha{x}+{p}? \\ $$
Commented by mnjuly1970 last updated on 26/Aug/24

$$\:\:{y}=\alpha{x}\:+\:\beta\:\:\underline{\underbrace{\lesseqgtr}} \\ $$
Commented by Frix last updated on 26/Aug/24
![I=∫_(−(π/2)) ^(π/2) (sin^2 x −2βsin x −2αxsin x +(αx+β)^2 )dx= =[((x−cos x sin x)/2)+2βcos x +2α(xcos x −sin x +(((αx+β)^3 )/(3α))]_(−(π/2)) ^(π/2) = =((α^2 π^3 )/(12))−4α+β^2 π+(π/2) The minimum occurs at α=((24)/π^3 )∧β=0 min I =((π^4 −96)/(2π^3 )) y=αx+β=((24x)/π^3 )](Q211013.png)
$${I}=\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{2}\beta\mathrm{sin}\:{x}\:−\mathrm{2}\alpha{x}\mathrm{sin}\:{x}\:+\left(\alpha{x}+\beta\right)^{\mathrm{2}} \right){dx}= \\ $$$$=\left[\frac{{x}−\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}}{\mathrm{2}}+\mathrm{2}\beta\mathrm{cos}\:{x}\:+\mathrm{2}\alpha\left({x}\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\:+\frac{\left(\alpha{x}+\beta\right)^{\mathrm{3}} }{\mathrm{3}\alpha}\right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} =\right. \\ $$$$=\frac{\alpha^{\mathrm{2}} \pi^{\mathrm{3}} }{\mathrm{12}}−\mathrm{4}\alpha+\beta^{\mathrm{2}} \pi+\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{minimum}\:\mathrm{occurs}\:\mathrm{at}\:\alpha=\frac{\mathrm{24}}{\pi^{\mathrm{3}} }\wedge\beta=\mathrm{0} \\ $$$$\mathrm{min}\:{I}\:=\frac{\pi^{\mathrm{4}} −\mathrm{96}}{\mathrm{2}\pi^{\mathrm{3}} } \\ $$$${y}=\alpha{x}+\beta=\frac{\mathrm{24}{x}}{\pi^{\mathrm{3}} } \\ $$
Commented by mnjuly1970 last updated on 26/Aug/24
$${grateful}\:{sir}\:{Frix} \\ $$
