
Question Number 210948 by cherokeesay last updated on 23/Aug/24
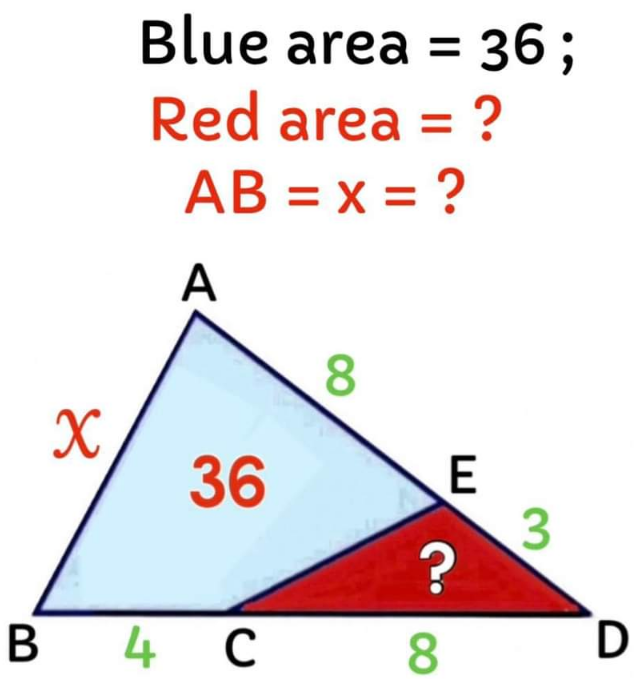
Commented by cherokeesay last updated on 23/Aug/24
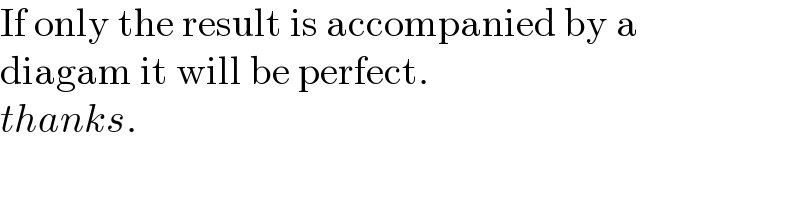
$$\mathrm{If}\:\mathrm{only}\:\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{accompanied}\:\mathrm{by}\:\mathrm{a} \\ $$$$\mathrm{diagam}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\mathrm{perfect}. \\ $$$${thanks}. \\ $$
Answered by A5T last updated on 23/Aug/24
![Let [BEC]=4y⇒[CED]=8y=? (([ABE])/([BED]=[BEC]+[CED]))=((36−4y)/(12y))=(8/3)⇒y=1 ⇒?=8y=8 ((11×12sin∠ADB)/2)=36+8=44⇒sin∠ADB=(2/3) ⇒cos∠ADB=((√5)/3) x^2 =11^2 +12^2 −2×11×4(√5)⇒x=(√(265−88(√5)))](Q210949.png)
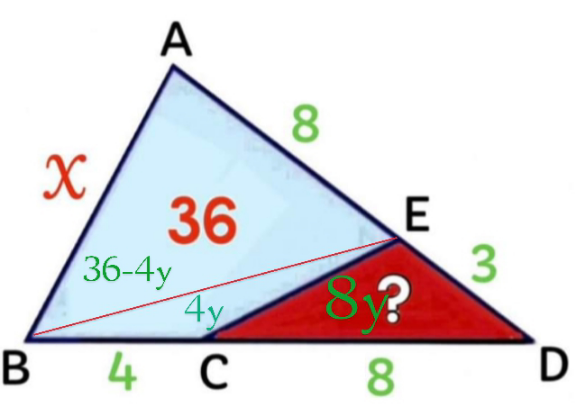
$${Let}\:\left[{BEC}\right]=\mathrm{4}{y}\Rightarrow\left[{CED}\right]=\mathrm{8}{y}=? \\ $$$$\frac{\left[{ABE}\right]}{\left[{BED}\right]=\left[{BEC}\right]+\left[{CED}\right]}=\frac{\mathrm{36}−\mathrm{4}{y}}{\mathrm{12}{y}}=\frac{\mathrm{8}}{\mathrm{3}}\Rightarrow{y}=\mathrm{1} \\ $$$$\Rightarrow?=\mathrm{8}{y}=\mathrm{8} \\ $$$$\frac{\mathrm{11}×\mathrm{12}{sin}\angle{ADB}}{\mathrm{2}}=\mathrm{36}+\mathrm{8}=\mathrm{44}\Rightarrow{sin}\angle{ADB}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{cos}\angle{ADB}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} =\mathrm{11}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} −\mathrm{2}×\mathrm{11}×\mathrm{4}\sqrt{\mathrm{5}}\Rightarrow{x}=\sqrt{\mathrm{265}−\mathrm{88}\sqrt{\mathrm{5}}} \\ $$
Commented by A5T last updated on 23/Aug/24
Commented by cherokeesay last updated on 23/Aug/24

$${thank}\:{you}\:{so}\:{much}\:! \\ $$
Answered by mr W last updated on 23/Aug/24
Commented by mr W last updated on 23/Aug/24
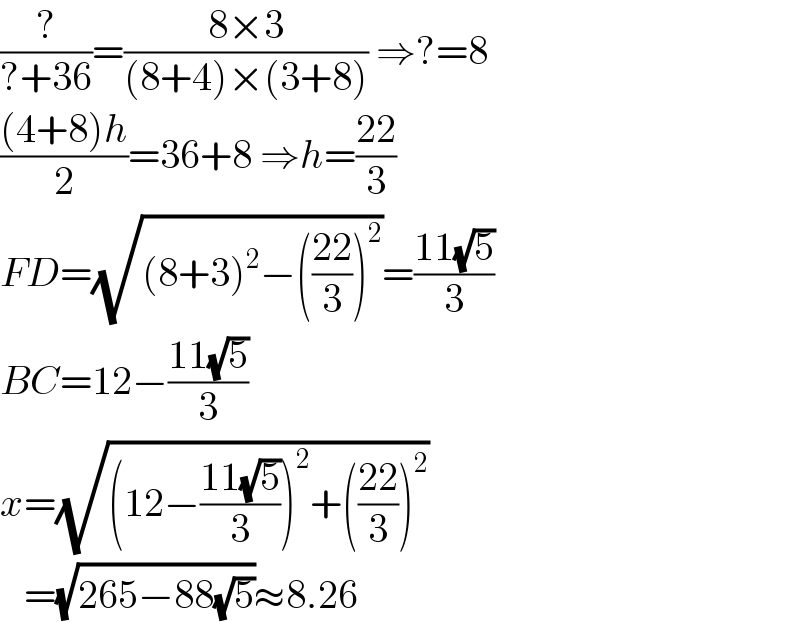
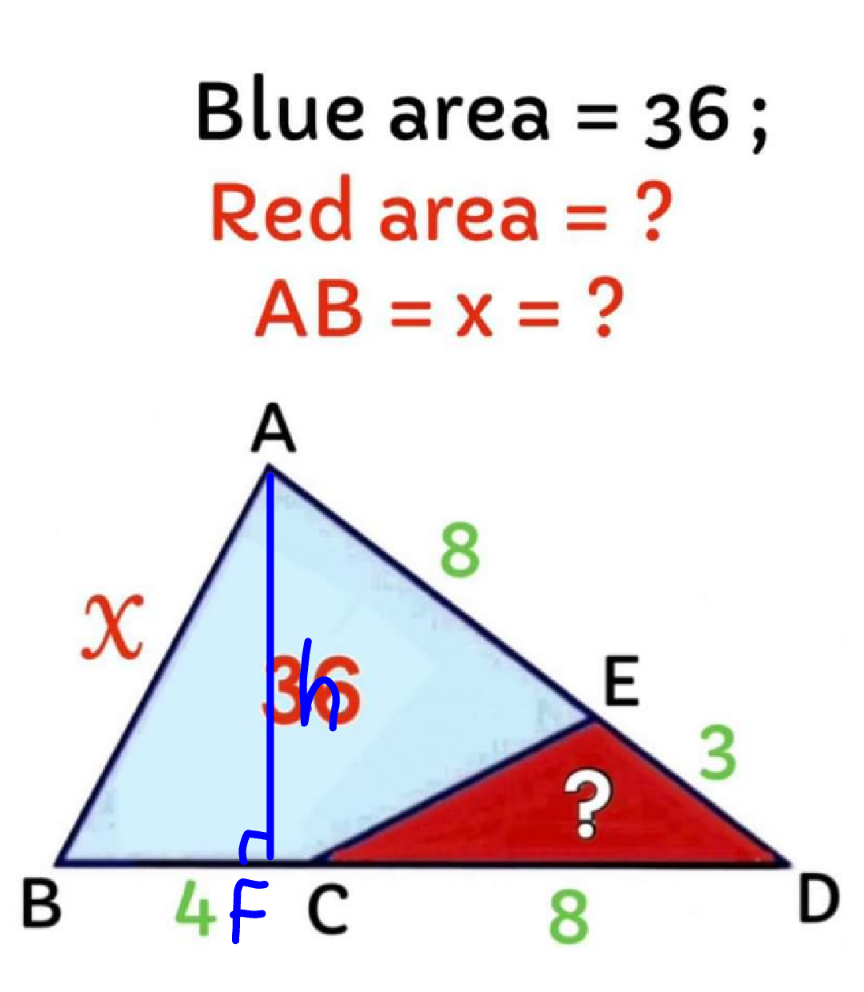
$$\frac{?}{?+\mathrm{36}}=\frac{\mathrm{8}×\mathrm{3}}{\left(\mathrm{8}+\mathrm{4}\right)×\left(\mathrm{3}+\mathrm{8}\right)}\:\Rightarrow?=\mathrm{8} \\ $$$$\frac{\left(\mathrm{4}+\mathrm{8}\right){h}}{\mathrm{2}}=\mathrm{36}+\mathrm{8}\:\Rightarrow{h}=\frac{\mathrm{22}}{\mathrm{3}} \\ $$$${FD}=\sqrt{\left(\mathrm{8}+\mathrm{3}\right)^{\mathrm{2}} −\left(\frac{\mathrm{22}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{11}\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${BC}=\mathrm{12}−\frac{\mathrm{11}\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${x}=\sqrt{\left(\mathrm{12}−\frac{\mathrm{11}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{22}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\sqrt{\mathrm{265}−\mathrm{88}\sqrt{\mathrm{5}}}\approx\mathrm{8}.\mathrm{26} \\ $$
