Question Number 210875 by peter frank last updated on 20/Aug/24

Answered by mahdipoor last updated on 20/Aug/24

$${get}\:{time}\:{is}\:{h}\::\:{m}\:\&\:{vertical}\:{line}\:{is}\:{refrence} \\ $$$${angle}\:{huur\_hand}\::\:\frac{\mathrm{360}}{\mathrm{12}}{h}+\frac{\mathrm{360}}{\mathrm{12}×\mathrm{60}}{m} \\ $$$${angle}\:{minute\_hand}\::\:\frac{\mathrm{360}}{\mathrm{60}}{m} \\ $$$$\Rightarrow\angle=\mid{h}−{m}\mid=\mid\mathrm{30}{h}−\mathrm{5}.\mathrm{5}{m}\mid\:{or}\:\mathrm{360}−\mid\mathrm{30}{h}−\mathrm{5}.\mathrm{5}{m}\mid \\ $$$${for}\:{example}:\:\mathrm{5}:\mathrm{45} \\ $$$$\Rightarrow\mid\mathrm{30}×\mathrm{5}−\mathrm{5}.\mathrm{5}×\mathrm{45}\mid=\mathrm{97}.\mathrm{5}\:{deg}=\mathrm{1}.\mathrm{702}\:{rad} \\ $$$$ \\ $$
Answered by efronzo1 last updated on 20/Aug/24

$$\:\:\theta\:=\:\frac{\mid\mathrm{60}.\mathrm{5}−\mathrm{11}.\mathrm{45}\mid^{\mathrm{o}} }{\mathrm{2}}\:=\:\mathrm{97}.\mathrm{5}^{\mathrm{o}} \\ $$
Answered by mr W last updated on 20/Aug/24
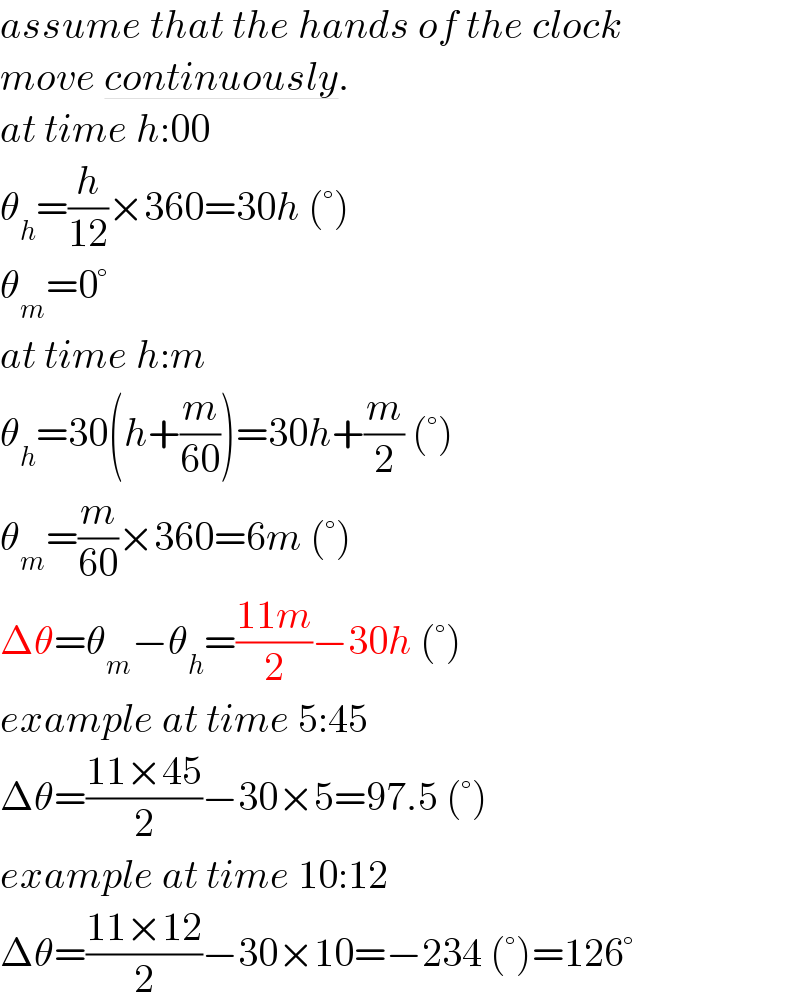
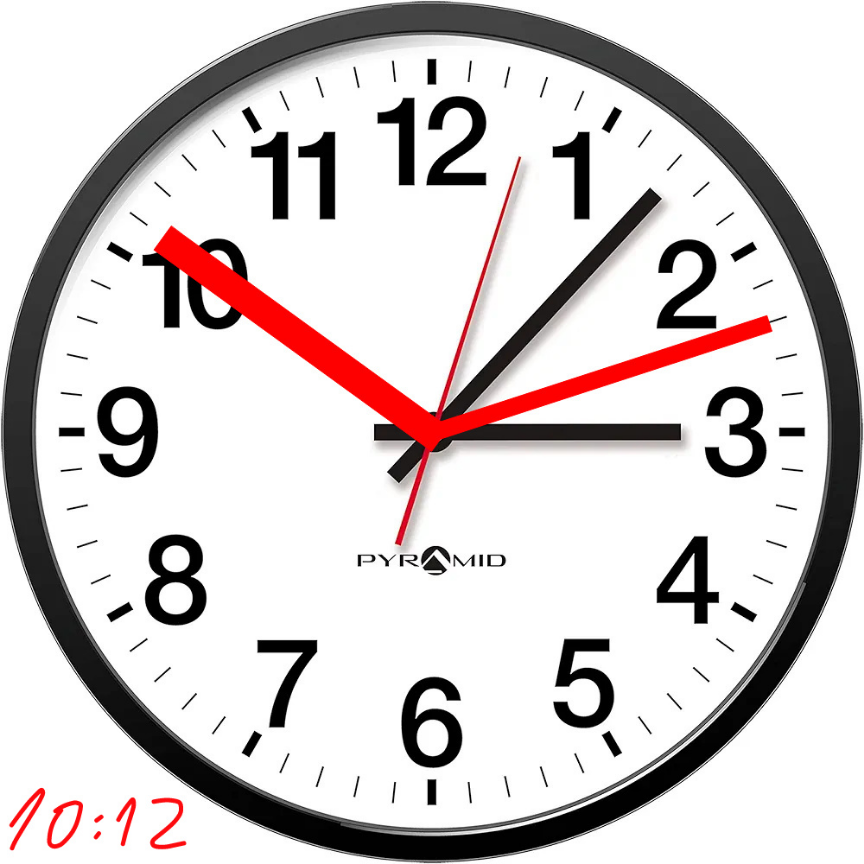
$${assume}\:{that}\:{the}\:{hands}\:{of}\:{the}\:{clock}\: \\ $$$${move}\:\underline{{continuously}}. \\ $$$${at}\:{time}\:{h}:\mathrm{00} \\ $$$$\theta_{{h}} =\frac{{h}}{\mathrm{12}}×\mathrm{360}=\mathrm{30}{h}\:\left(°\right) \\ $$$$\theta_{{m}} =\mathrm{0}° \\ $$$${at}\:{time}\:{h}:{m} \\ $$$$\theta_{{h}} =\mathrm{30}\left({h}+\frac{{m}}{\mathrm{60}}\right)=\mathrm{30}{h}+\frac{{m}}{\mathrm{2}}\:\left(°\right) \\ $$$$\theta_{{m}} =\frac{{m}}{\mathrm{60}}×\mathrm{360}=\mathrm{6}{m}\:\left(°\right) \\ $$$$\Delta\theta=\theta_{{m}} −\theta_{{h}} =\frac{\mathrm{11}{m}}{\mathrm{2}}−\mathrm{30}{h}\:\left(°\right) \\ $$$${example}\:{at}\:{time}\:\mathrm{5}:\mathrm{45} \\ $$$$\Delta\theta=\frac{\mathrm{11}×\mathrm{45}}{\mathrm{2}}−\mathrm{30}×\mathrm{5}=\mathrm{97}.\mathrm{5}\:\left(°\right) \\ $$$${example}\:{at}\:{time}\:\mathrm{10}:\mathrm{12} \\ $$$$\Delta\theta=\frac{\mathrm{11}×\mathrm{12}}{\mathrm{2}}−\mathrm{30}×\mathrm{10}=−\mathrm{234}\:\left(°\right)=\mathrm{126}° \\ $$
Commented by peter frank last updated on 22/Aug/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 20/Aug/24

Commented by mr W last updated on 21/Aug/24

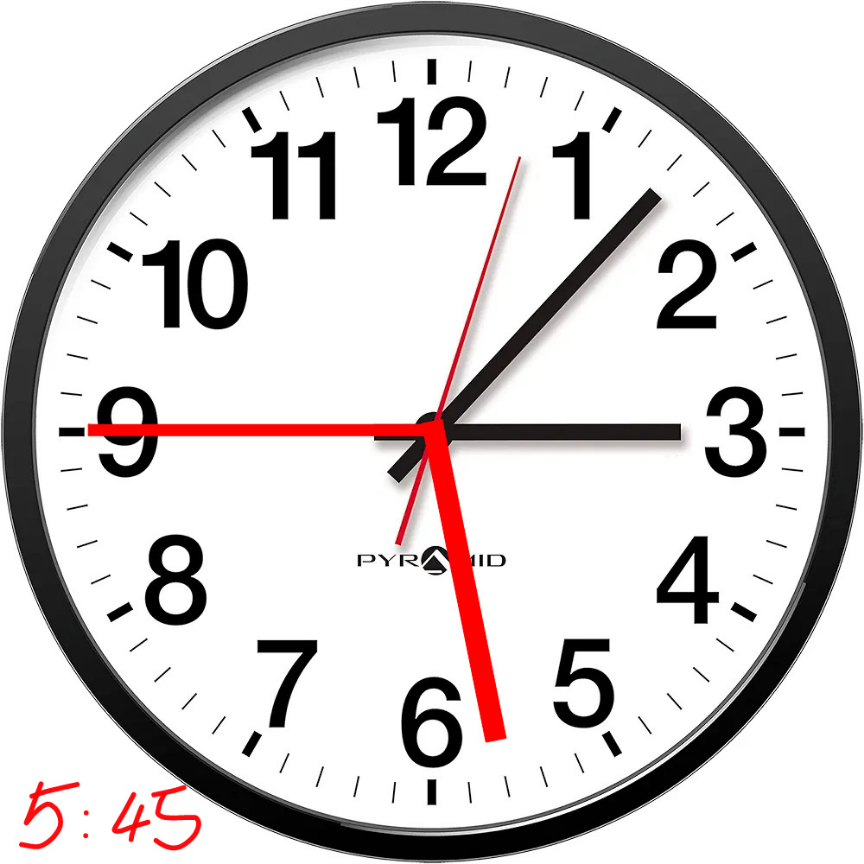
$${now}\:{let}'{s}\:{look}\:{at}\:{a}\:{real}\:{clock}. \\ $$$${on}\:{a}\:{mechanically}\:{driven}\:{clock}\:{the} \\ $$$${hands}\:{don}'{t}\:{move}\:{continuously}.\: \\ $$$${they}\:{can}\:{only}\:{have}\:\mathrm{60}\:{possible} \\ $$$${positions}\:{around}\:{the}\:{circle}.\:{for} \\ $$$${example}\:{from}\:\mathrm{3}:\mathrm{00}\:{to}\:\mathrm{3}:\mathrm{12}\:{the}\:{hour} \\ $$$${hand}\:{remains}\:{in}\:{the}\:{same}\:{position} \\ $$$${as}\:{at}\:\mathrm{3}:\mathrm{00}.\:{the}\:{picture}\:{above}\:{shows} \\ $$$${e}.{g}.\:{the}\:{time}\:\mathrm{3}:\mathrm{07}:\mathrm{03}. \\ $$$${in}\:{following}\:{picture}\:{the}\:{red}\:{hour} \\ $$$${hand}\:{and}\:{red}\:{minute}\:{hand}\:{show} \\ $$$${the}\:{time}\:\mathrm{5}:\mathrm{45}.\:{the}\:{angle}\:{between} \\ $$$${them}\:{is}\:\mathrm{17}×\mathrm{6}=\mathrm{102}°\:\left(\neq\mathrm{97}.\mathrm{5}°\right). \\ $$
Commented by mr W last updated on 20/Aug/24
Commented by mr W last updated on 20/Aug/24

$${following}\:{picture}\:{shows}\:{the}\:{time} \\ $$$$\mathrm{10}:\mathrm{12}.\:{the}\:{angle}\:{between}\:{the}\:{minute} \\ $$$${hand}\:{and}\:{hour}\:{hand}\:{is} \\ $$$$\mathrm{21}×\mathrm{6}=\mathrm{126}\:° \\ $$
Commented by mr W last updated on 20/Aug/24