
Question Number 210695 by cherokeesay last updated on 16/Aug/24

Commented by A5T last updated on 17/Aug/24
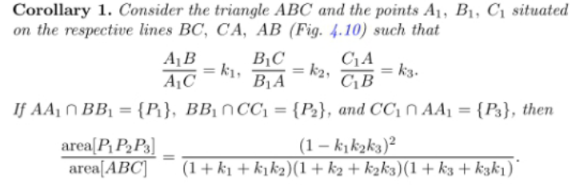
Answered by mr W last updated on 17/Aug/24
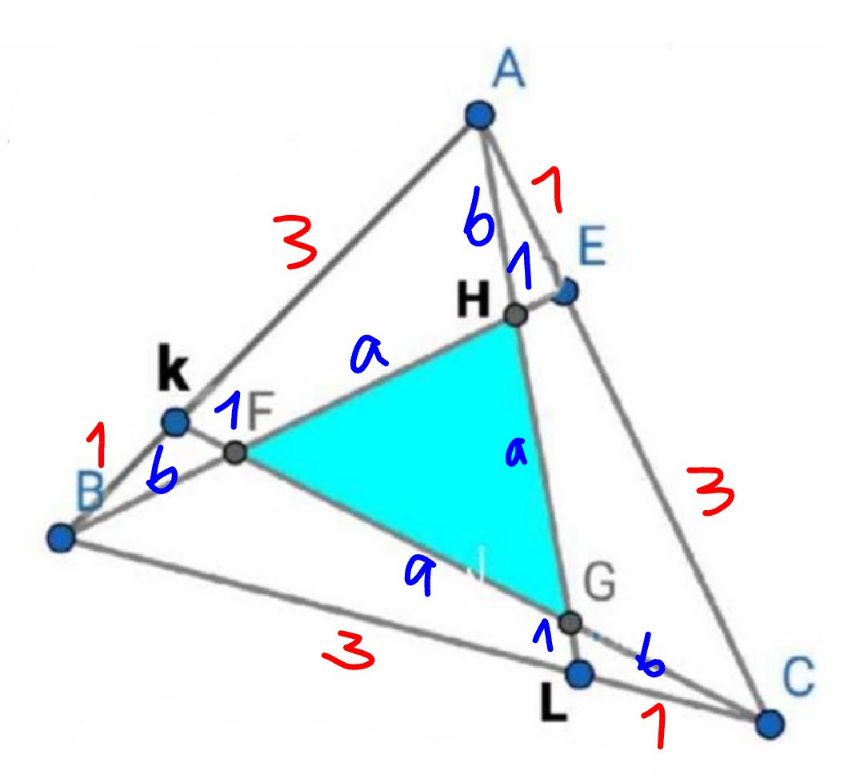
Commented by mr W last updated on 17/Aug/24
![the numbers in the figure mean the ratios of the corresponding segments, i.e. 1:3, 1:a:b. we have (1/a)×(a/b)×(4/1)=1 ⇒b=4 (1/(a+b))×(3/1)×(4/1)=1 ⇒a+b=12 ⇒a=8 [ABE]=(1/4)[ABC] [AHE]=(1/(1+a+b))×[ABE]=(1/(13))×(1/4)[ABC]=(1/(52))[ABC] [HFG]=[ABC]−3×(1/4)[ABC]+3×(1/(52))[ABC] =(7/(26))[ABC]=(7/(26))×26=7 ✓](Q210705.png)
$${the}\:{numbers}\:{in}\:{the}\:{figure}\:{mean}\:{the} \\ $$$${ratios}\:{of}\:{the}\:{corresponding}\:{segments}, \\ $$$${i}.{e}.\:\mathrm{1}:\mathrm{3},\:\mathrm{1}:{a}:{b}. \\ $$$${we}\:{have} \\ $$$$\frac{\mathrm{1}}{{a}}×\frac{{a}}{{b}}×\frac{\mathrm{4}}{\mathrm{1}}=\mathrm{1}\:\Rightarrow{b}=\mathrm{4} \\ $$$$\frac{\mathrm{1}}{{a}+{b}}×\frac{\mathrm{3}}{\mathrm{1}}×\frac{\mathrm{4}}{\mathrm{1}}=\mathrm{1}\:\Rightarrow{a}+{b}=\mathrm{12}\:\Rightarrow{a}=\mathrm{8} \\ $$$$\left[{ABE}\right]=\frac{\mathrm{1}}{\mathrm{4}}\left[{ABC}\right] \\ $$$$\left[{AHE}\right]=\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}×\left[{ABE}\right]=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\mathrm{1}}{\mathrm{4}}\left[{ABC}\right]=\frac{\mathrm{1}}{\mathrm{52}}\left[{ABC}\right] \\ $$$$\left[{HFG}\right]=\left[{ABC}\right]−\mathrm{3}×\frac{\mathrm{1}}{\mathrm{4}}\left[{ABC}\right]+\mathrm{3}×\frac{\mathrm{1}}{\mathrm{52}}\left[{ABC}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{26}}\left[{ABC}\right]=\frac{\mathrm{7}}{\mathrm{26}}×\mathrm{26}=\mathrm{7}\:\checkmark \\ $$
Commented by cherokeesay last updated on 17/Aug/24
$${so}\:{nice}\:!\:{thank}\:{you}\:{sir}\:! \\ $$
Commented by cherokeesay last updated on 17/Aug/24

$${thank}\:{you}\:! \\ $$
