Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

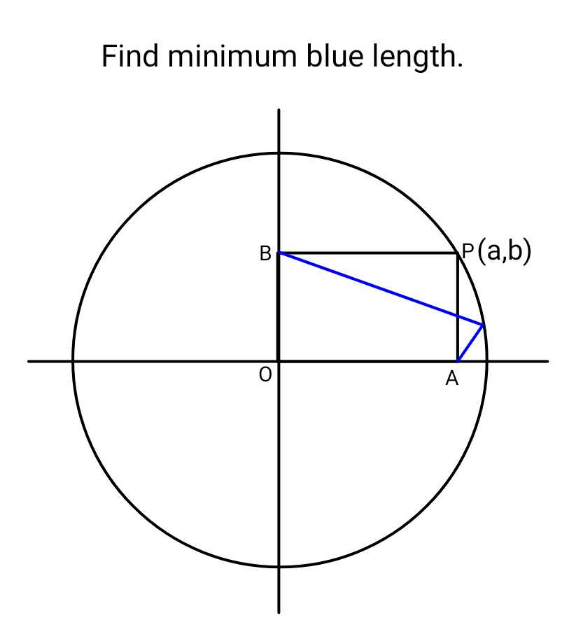
Question Number 210694 by ajfour last updated on 16/Aug/24

Answered by mr W last updated on 17/Aug/24

Commented by mr W last updated on 17/Aug/24

R=(√(a^2 +b^2 )) ((sin α)/b)=((sin ((π/2)−θ+α))/R)=((cos θ cos α+sin θ sin α)/R) (R/b)=((cos θ )/(tan α))+sin θ ⇒(1/(tan α))=((R/b)−sin θ)(1/(cos θ)) ((sin α)/a)=((sin (θ+α))/R)=((sin θ cos α+cos θ sin α)/R) (R/a)=((sin θ)/(tan α))+cos θ ⇒(1/(tan α))=((R/a)−cos θ)(1/(sin θ)) ((R/b)−sin θ)(1/(cos θ))=((R/a)−cos θ)(1/(sin θ)) (R/a) cos θ−(R/b) sin θ=cos 2θ ⇒((cos θ)/(cos φ))−((sin θ)/(sin φ))=cos 2θ L_(min) =(√(a^2 +R^2 −2aR cos θ))+(√(b^2 +R^2 −2bR sin θ)) (L_(min) /R)=(√(1+cos^2 φ−2 cos φ cos θ))+(√(1+sin^2 φ−2 sin φ sin θ))

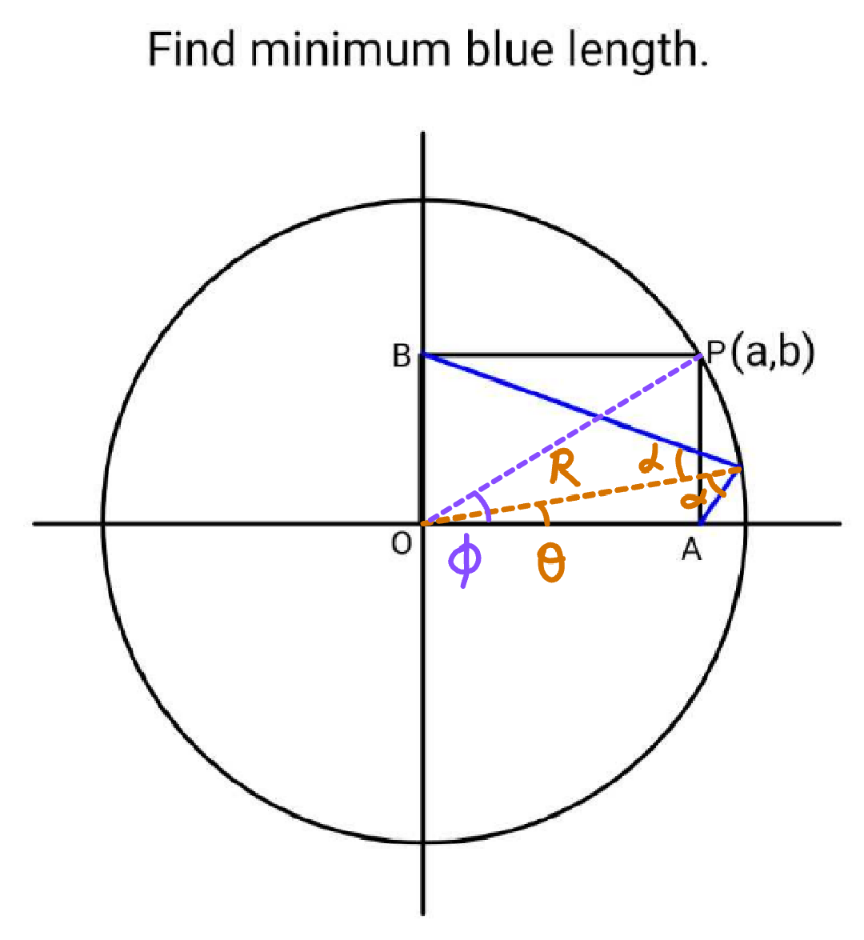
$${R}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{sin}\:\alpha}{{b}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta+\alpha\right)}{{R}}=\frac{\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\theta\:\mathrm{sin}\:\alpha}{{R}} \\ $$$$\frac{{R}}{{b}}=\frac{\mathrm{cos}\:\theta\:}{\mathrm{tan}\:\alpha}+\mathrm{sin}\:\theta \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\left(\frac{{R}}{{b}}−\mathrm{sin}\:\theta\right)\frac{\mathrm{1}}{\mathrm{cos}\:\theta} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{a}}=\frac{\mathrm{sin}\:\left(\theta+\alpha\right)}{{R}}=\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha}{{R}} \\ $$$$\frac{{R}}{{a}}=\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha}+\mathrm{cos}\:\theta \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\left(\frac{{R}}{{a}}−\mathrm{cos}\:\theta\right)\frac{\mathrm{1}}{\mathrm{sin}\:\theta} \\ $$$$\left(\frac{{R}}{{b}}−\mathrm{sin}\:\theta\right)\frac{\mathrm{1}}{\mathrm{cos}\:\theta}=\left(\frac{{R}}{{a}}−\mathrm{cos}\:\theta\right)\frac{\mathrm{1}}{\mathrm{sin}\:\theta} \\ $$$$\frac{{R}}{{a}}\:\mathrm{cos}\:\theta−\frac{{R}}{{b}}\:\mathrm{sin}\:\theta=\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\phi}−\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:\phi}=\mathrm{cos}\:\mathrm{2}\theta \\ $$$$ \\ $$$${L}_{{min}} =\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{aR}\:\mathrm{cos}\:\theta}+\sqrt{{b}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{bR}\:\mathrm{sin}\:\theta} \\ $$$$\frac{{L}_{{min}} }{{R}}=\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\phi−\mathrm{2}\:\mathrm{cos}\:\phi\:\mathrm{cos}\:\theta}+\sqrt{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\phi−\mathrm{2}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\theta} \\ $$

Commented by mr W last updated on 17/Aug/24

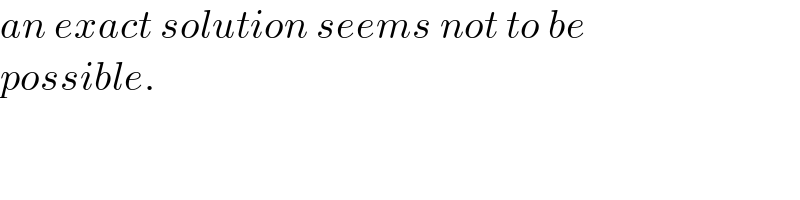
an exact solution seems not to be possible.

$${an}\:{exact}\:{solution}\:{seems}\:{not}\:{to}\:{be} \\ $$$${possible}. \\ $$

Commented by ajfour last updated on 17/Aug/24

((sin α)/b)=((sin ((π/2)+θ−α))/R)=((cos θ cos α−sin θ sin α)/R) (R/a)=((sin θ)/(tan α))−cos θ (((sin θ)/m)−(R/a))^2 =1−sin^2 θ L_(min) =(√(a^2 +R^2 −2aR cos θ))+(√(b^2 +R^2 −2bR sin θ)) =(√(a^2 +R^2 −2R(((asin θ)/m)−R))) +(√(b^2 +R^2 −2bRsin θ)) =(√(a^2 +3R^2 −((2aR)/m)sin θ))+(√(b^2 +R^2 −2bRsin θ)) .......

$$\frac{\mathrm{sin}\:\alpha}{{b}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\theta−\alpha\right)}{{R}}=\frac{\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\theta\:\mathrm{sin}\:\alpha}{{R}} \\ $$$$\frac{{R}}{{a}}=\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha}−\mathrm{cos}\:\theta \\ $$$$\left(\frac{\mathrm{sin}\:\theta}{{m}}−\frac{{R}}{{a}}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${L}_{{min}} =\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{aR}\:\mathrm{cos}\:\theta}+\sqrt{{b}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{bR}\:\mathrm{sin}\:\theta} \\ $$$$\:\:=\sqrt{{a}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{R}\left(\frac{{a}\mathrm{sin}\:\theta}{{m}}−{R}\right)} \\ $$$$\:\:\:\:\:\:\:\:+\sqrt{{b}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{bR}\mathrm{sin}\:\theta} \\ $$$$=\sqrt{{a}^{\mathrm{2}} +\mathrm{3}{R}^{\mathrm{2}} −\frac{\mathrm{2}{aR}}{{m}}\mathrm{sin}\:\theta}+\sqrt{{b}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{bR}\mathrm{sin}\:\theta} \\ $$$$....... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com