
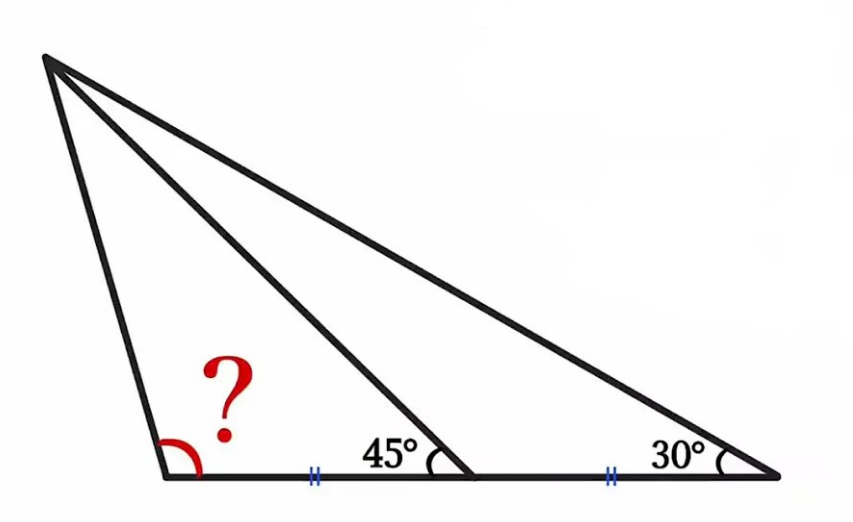
Question Number 210667 by mr W last updated on 15/Aug/24
Answered by ajfour last updated on 16/Aug/24

$${let}\:{C}\:{be}\:{origin}\:\:{and}\:{A}\left({p},{q}\right) \\ $$$${q}=\frac{{p}}{\:\sqrt{\mathrm{3}}} \\ $$$${q}={p}−{a} \\ $$$$\mathrm{0}−{q}={m}\left(\mathrm{2}{a}−{p}\right) \\ $$$$\Rightarrow\:\:{m}=−\frac{{q}}{\mathrm{2}{a}−{p}}=−\frac{{q}}{{p}−\mathrm{2}{q}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta_{?} =−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\theta_{?} =\pi−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$
Commented by mr W last updated on 16/Aug/24
��
Answered by A5T last updated on 15/Aug/24
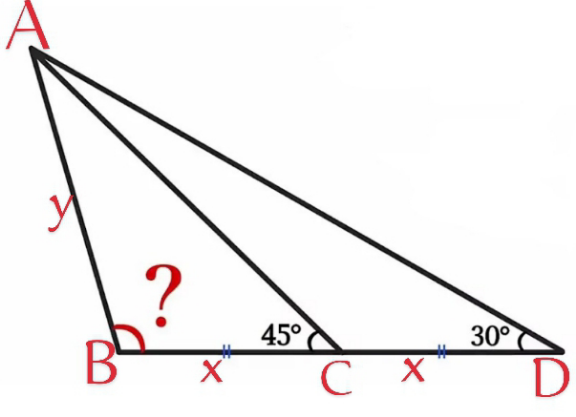
Commented by A5T last updated on 15/Aug/24
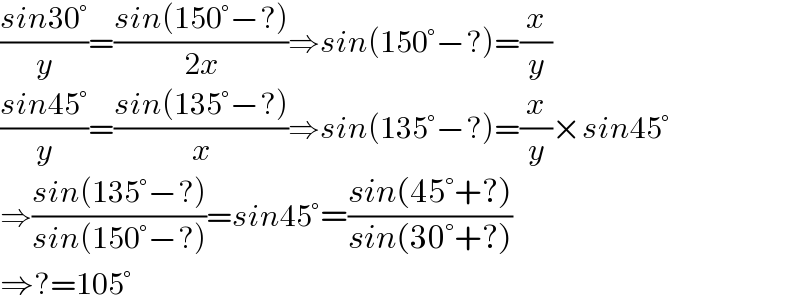
$$\frac{{sin}\mathrm{30}°}{{y}}=\frac{{sin}\left(\mathrm{150}°−?\right)}{\mathrm{2}{x}}\Rightarrow{sin}\left(\mathrm{150}°−?\right)=\frac{{x}}{{y}} \\ $$$$\frac{{sin}\mathrm{45}°}{{y}}=\frac{{sin}\left(\mathrm{135}°−?\right)}{{x}}\Rightarrow{sin}\left(\mathrm{135}°−?\right)=\frac{{x}}{{y}}×{sin}\mathrm{45}° \\ $$$$\Rightarrow\frac{{sin}\left(\mathrm{135}°−?\right)}{{sin}\left(\mathrm{150}°−?\right)}={sin}\mathrm{45}°=\frac{{sin}\left(\mathrm{45}°+?\right)}{{sin}\left(\mathrm{30}°+?\right)} \\ $$$$\Rightarrow?=\mathrm{105}° \\ $$
Commented by mr W last updated on 15/Aug/24
��
Answered by mr W last updated on 15/Aug/24
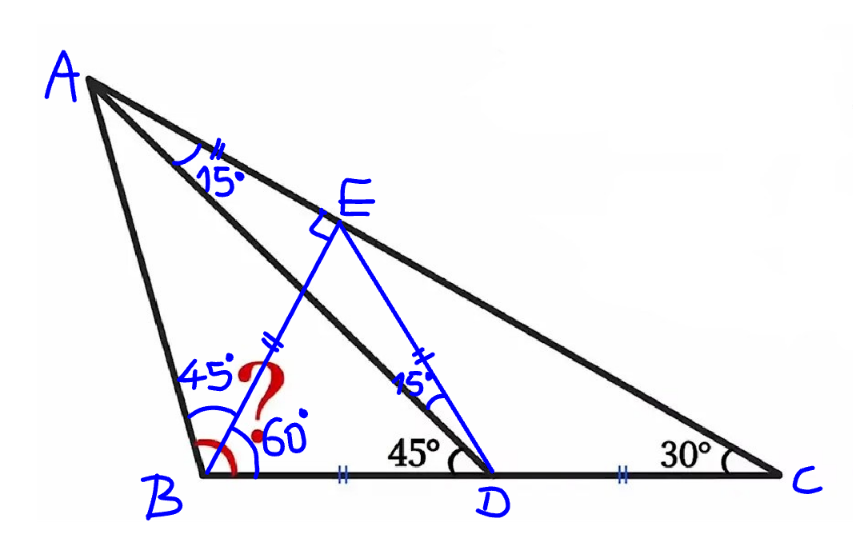
Commented by mr W last updated on 15/Aug/24

$$?=\mathrm{60}+\mathrm{45}=\mathrm{105}° \\ $$
