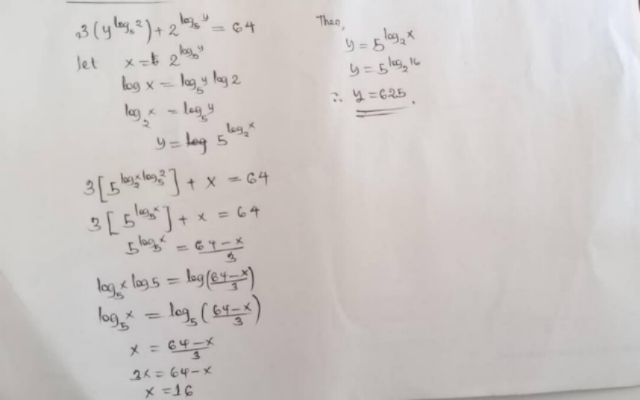Question Number 210606 by peter frank last updated on 13/Aug/24
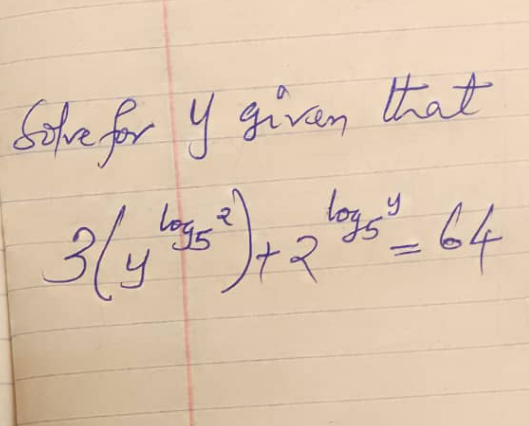
Answered by A5T last updated on 14/Aug/24
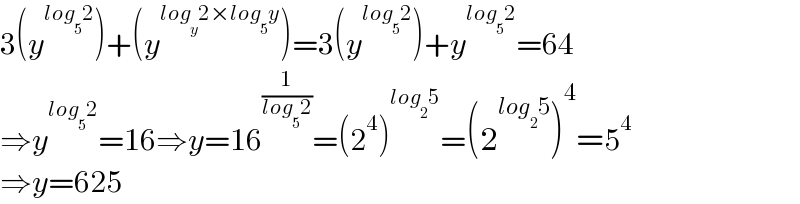
$$\mathrm{3}\left({y}^{{log}_{\mathrm{5}} \mathrm{2}} \right)+\left({y}^{{log}_{{y}} \mathrm{2}×{log}_{\mathrm{5}} {y}} \right)=\mathrm{3}\left({y}^{{log}_{\mathrm{5}} \mathrm{2}} \right)+{y}^{{log}_{\mathrm{5}} \mathrm{2}} =\mathrm{64} \\ $$$$\Rightarrow{y}^{{log}_{\mathrm{5}} \mathrm{2}} =\mathrm{16}\Rightarrow{y}=\mathrm{16}^{\frac{\mathrm{1}}{{log}_{\mathrm{5}} \mathrm{2}}} =\left(\mathrm{2}^{\mathrm{4}} \right)^{{log}_{\mathrm{2}} \mathrm{5}} =\left(\mathrm{2}^{{log}_{\mathrm{2}} \mathrm{5}} \right)^{\mathrm{4}} =\mathrm{5}^{\mathrm{4}} \\ $$$$\Rightarrow{y}=\mathrm{625} \\ $$
Commented by peter frank last updated on 14/Aug/24
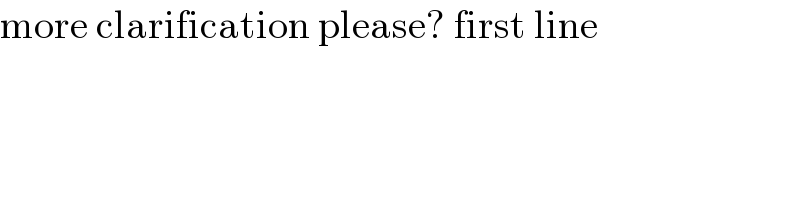
$$\mathrm{more}\:\mathrm{clarification}\:\mathrm{please}?\:\mathrm{first}\:\mathrm{line} \\ $$
Commented by A5T last updated on 14/Aug/24
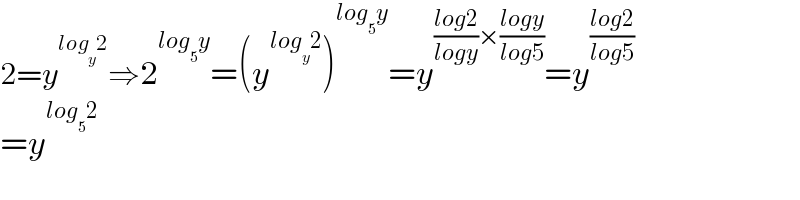
$$\mathrm{2}={y}^{{log}_{{y}} \mathrm{2}} \Rightarrow\mathrm{2}^{{log}_{\mathrm{5}} {y}} =\left({y}^{{log}_{{y}} \mathrm{2}} \right)^{{log}_{\mathrm{5}} {y}} ={y}^{\frac{{log}\mathrm{2}}{{logy}}×\frac{{logy}}{{log}\mathrm{5}}} ={y}^{\frac{{log}\mathrm{2}}{{log}\mathrm{5}}} \\ $$$$={y}^{{log}_{\mathrm{5}} \mathrm{2}} \\ $$
Answered by Spillover last updated on 14/Aug/24