
Question Number 210496 by lmcp1203 last updated on 11/Aug/24
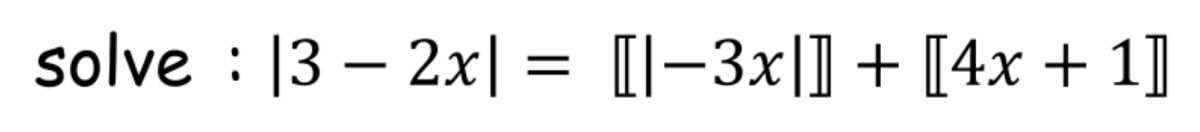
Commented by mr W last updated on 11/Aug/24
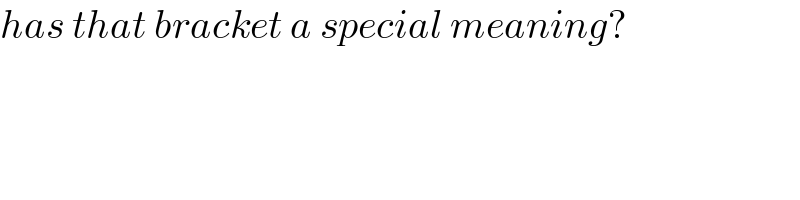
$${has}\:{that}\:{bracket}\:{a}\:{special}\:{meaning}? \\ $$
Commented by lmcp1203 last updated on 11/Aug/24
$${please}\:{help}\:{me}\:{thanks} \\ $$
Commented by klipto last updated on 11/Aug/24

$$\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{should}}\:\boldsymbol{\mathrm{be}}\:\boldsymbol{\mathrm{floor}}\:\boldsymbol{\mathrm{function}} \\ $$
Commented by lmcp1203 last updated on 11/Aug/24

$${yes} \\ $$
Answered by Frix last updated on 11/Aug/24
![f(x)=∣3−2x∣= { ((3−2x, x≤(3/2))),((2x−3, x>(3/2))) :} g(x)=⌊∣−3x∣⌋+⌊4x+1⌋= = { ((1+⌊−3x⌋+⌊4x⌋, x≤0)),((1+⌊3x⌋+⌊4x⌋, x>0)) :} ⇒ f(x)≥0, x∈R f((3/2))=0 g(x)≤0, x<0; g(x)≥1; x≥0 ⇒ possible solutions for x∈]0, (3/2)[ ⇒ 3−2x=1+⌊3x⌋+⌊4x⌋ h(x)=2x+⌊3x⌋+⌊4x⌋=2 lim_(x→1/3^− ) h(x) =−(1/3) lim_(x→1/3^+ ) h(x) =+(2/3) ⇒ no solution](Q210521.png)
$${f}\left({x}\right)=\mid\mathrm{3}−\mathrm{2}{x}\mid=\begin{cases}{\mathrm{3}−\mathrm{2}{x},\:{x}\leqslant\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{2}{x}−\mathrm{3},\:{x}>\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$$${g}\left({x}\right)=\lfloor\mid−\mathrm{3}{x}\mid\rfloor+\lfloor\mathrm{4}{x}+\mathrm{1}\rfloor= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\begin{cases}{\mathrm{1}+\lfloor−\mathrm{3}{x}\rfloor+\lfloor\mathrm{4}{x}\rfloor,\:{x}\leqslant\mathrm{0}}\\{\mathrm{1}+\lfloor\mathrm{3}{x}\rfloor+\lfloor\mathrm{4}{x}\rfloor,\:{x}>\mathrm{0}}\end{cases} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)\geqslant\mathrm{0},\:{x}\in\mathbb{R}\:\:\:\:\:{f}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${g}\left({x}\right)\leqslant\mathrm{0},\:{x}<\mathrm{0};\:\:\:\:\:{g}\left({x}\right)\geqslant\mathrm{1};\:{x}\geqslant\mathrm{0} \\ $$$$\left.\Rightarrow\:\mathrm{possible}\:\mathrm{solutions}\:\mathrm{for}\:{x}\in\right]\mathrm{0},\:\frac{\mathrm{3}}{\mathrm{2}}\left[\right. \\ $$$$\Rightarrow \\ $$$$\mathrm{3}−\mathrm{2}{x}=\mathrm{1}+\lfloor\mathrm{3}{x}\rfloor+\lfloor\mathrm{4}{x}\rfloor \\ $$$${h}\left({x}\right)=\mathrm{2}{x}+\lfloor\mathrm{3}{x}\rfloor+\lfloor\mathrm{4}{x}\rfloor=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{1}/\mathrm{3}^{−} } {\mathrm{lim}}\:{h}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}/\mathrm{3}^{+} } {\mathrm{lim}}\:{h}\left({x}\right)\:=+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$
Commented by lmcp1203 last updated on 12/Aug/24

$${thanks}\:{sir} \\ $$
