
Question Number 210441 by universe last updated on 09/Aug/24
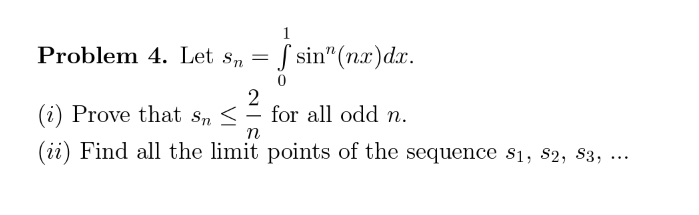
Answered by aleks041103 last updated on 09/Aug/24
![(i) for odd n, the function sin^n (nx) is similar to sin(x) with the fact that the primitive function oscilates between 0 and the maximal possible value ∫_0 ^( π/n) sin^n (nx)dx = (1/n)∫_0 ^( π) sin^n (x)dx≤ ≤(1/n)∫_0 ^( π) sin(x)dx=(2/n) s_n =F_n (1)−F_n (0) for odd n we have F_n (x)∈[0,2/n] then s_n ≤(2/n), odd n.](Q210460.png)
$$\left({i}\right)\: \\ $$$${for}\:{odd}\:{n},\:{the}\:{function}\:{sin}^{{n}} \left({nx}\right)\:{is}\:{similar} \\ $$$${to}\:{sin}\left({x}\right)\:{with}\:{the}\:{fact}\:{that}\:{the}\:{primitive}\:{function}\:{oscilates} \\ $$$${between}\:\mathrm{0}\:{and}\:{the}\:{maximal}\:{possible}\:{value} \\ $$$$\int_{\mathrm{0}} ^{\:\pi/{n}} {sin}^{{n}} \left({nx}\right){dx}\:=\:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\pi} {sin}^{{n}} \left({x}\right){dx}\leqslant \\ $$$$\leqslant\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\pi} {sin}\left({x}\right){dx}=\frac{\mathrm{2}}{{n}} \\ $$$$ \\ $$$${s}_{{n}} ={F}_{{n}} \left(\mathrm{1}\right)−{F}_{{n}} \left(\mathrm{0}\right) \\ $$$${for}\:{odd}\:{n}\:{we}\:{have}\:{F}_{{n}} \left({x}\right)\in\left[\mathrm{0},\mathrm{2}/{n}\right] \\ $$$${then}\:{s}_{{n}} \leqslant\frac{\mathrm{2}}{{n}},\:{odd}\:{n}. \\ $$
Answered by aleks041103 last updated on 09/Aug/24
![(ii) for even n: ∫_0 ^( 1) sin^n (nx)dx=(1/n)∫_0 ^( n) sin^n (x)dx= =(1/n)[Σ_(k=0) ^(⌊n/π⌋−1) ∫_(πk) ^( π(k+1)) sin^n (x)dx + ∫_(π⌊n/π⌋) ^( n) sin^n (x)dx]= =(1/n)(⌊(n/π)⌋+c)∫_0 ^( π) sin^n (x)dx where 0<c<1. now let I_n =∫_0 ^( π) sin^(2n) (x)dx= =∫_0 ^( π) sin^(2n−2) (x)dx − ∫_0 ^( π) cos(x)d(((sin^(2n−1) (x))/(2n−1)))dx= =I_(n−1) −[((sin^(2n−1) (x)cos(x))/(2n−1))]_0 ^π −(1/(2n−1))∫_0 ^( π) sin^(2n) (x)dx= =I_(n−1) −(1/(2n−1))I_n ⇒I_(n−1) =((2n)/(2n−1))I_n ⇒I_n =((2n−1)/(2n))I_(n−1) ⇒I_n =(((2n−1)(2n−3)...3.1)/((2n)(2n−2)...4.2))I_0 I_0 =∫_0 ^( π) dx=π ⇒I_n =(((2n−1)!!)/((2n)!!))π (2n)!!=2^n n! (2n−1)!!=(((2n)!)/((2n)!!))=(((2n)!)/(2^n n!)) ⇒I_n =(((2n)!)/(4^n (n!)^2 ))π ⇒s_(2n) =(1/(2n))(⌊((2n)/π)⌋+c_n )I_n =(π/(2n))(⌊((2n)/π)⌋+c_n )(((2n)!)/(4^n (n!)^2 )) Stirling: x! ∼ (√(2πx)) ((x/e))^x ⇒(2n)! ∼ (√(4πn))(((2n)/e))^(2n) =(√(4πn ))4^n ((n/e))^(2n) ⇒(n!)^2 ∼ 2πn((n/e))^(2n) ⇒s_(2n) =(π/(2n))(⌊((2n)/π)⌋+c_n )(((2n)!)/(4^n (n!)^2 )) ∼ (π/(2n))(⌊((2n)/π)⌋+c_n )((√(4πn))/(2πn)) ⇒s_(2n) ∼ (π/(2n))(⌊((2n)/π)⌋+c_n )(1/( (√(πn)))) it is easy to see that (π/(2n))⌊((2n)/π)⌋∼1 ⇒s_(2n) ∼ (1/( (√(πn)))) ⇒s_(2n) →0 from (i) we have 0<s_(2n+1) <(2/(2n+1)) ⇒s_(2n+1) →0 ⇒s_n →0 ⇒ the only limiting point is 0.](Q210461.png)
$$\left({ii}\right)\:{for}\:{even}\:{n}: \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} {sin}^{{n}} \left({nx}\right){dx}=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:{n}} {sin}^{{n}} \left({x}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{{n}}\left[\underset{{k}=\mathrm{0}} {\overset{\lfloor{n}/\pi\rfloor−\mathrm{1}} {\sum}}\int_{\pi{k}} ^{\:\pi\left({k}+\mathrm{1}\right)} {sin}^{{n}} \left({x}\right){dx}\:+\:\int_{\pi\lfloor{n}/\pi\rfloor} ^{\:{n}} {sin}^{{n}} \left({x}\right){dx}\right]= \\ $$$$=\frac{\mathrm{1}}{{n}}\left(\lfloor\frac{{n}}{\pi}\rfloor+{c}\right)\int_{\mathrm{0}} ^{\:\pi} {sin}^{{n}} \left({x}\right){dx} \\ $$$${where}\:\mathrm{0}<{c}<\mathrm{1}. \\ $$$$ \\ $$$${now}\:{let} \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\:\pi} {sin}^{\mathrm{2}{n}} \left({x}\right){dx}= \\ $$$$=\int_{\mathrm{0}} ^{\:\pi} {sin}^{\mathrm{2}{n}−\mathrm{2}} \left({x}\right){dx}\:−\:\int_{\mathrm{0}} ^{\:\pi} {cos}\left({x}\right){d}\left(\frac{{sin}^{\mathrm{2}{n}−\mathrm{1}} \left({x}\right)}{\mathrm{2}{n}−\mathrm{1}}\right){dx}= \\ $$$$={I}_{{n}−\mathrm{1}} −\left[\frac{{sin}^{\mathrm{2}{n}−\mathrm{1}} \left({x}\right){cos}\left({x}\right)}{\mathrm{2}{n}−\mathrm{1}}\right]_{\mathrm{0}} ^{\pi} −\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\:\pi} {sin}^{\mathrm{2}{n}} \left({x}\right){dx}= \\ $$$$={I}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}{I}_{{n}} \\ $$$$\Rightarrow{I}_{{n}−\mathrm{1}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}−\mathrm{1}}{I}_{{n}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}{I}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{3}\right)...\mathrm{3}.\mathrm{1}}{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}−\mathrm{2}\right)...\mathrm{4}.\mathrm{2}}{I}_{\mathrm{0}} \\ $$$${I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\:\pi} {dx}=\pi \\ $$$$\Rightarrow{I}_{{n}} =\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)!!}{\left(\mathrm{2}{n}\right)!!}\pi \\ $$$$\left(\mathrm{2}{n}\right)!!=\mathrm{2}^{{n}} {n}! \\ $$$$\left(\mathrm{2}{n}−\mathrm{1}\right)!!=\frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}{n}\right)!!}=\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{{n}} {n}!} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{4}^{{n}} \left({n}!\right)^{\mathrm{2}} }\pi \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}} =\frac{\mathrm{1}}{\mathrm{2}{n}}\left(\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor+{c}_{{n}} \right){I}_{{n}} =\frac{\pi}{\mathrm{2}{n}}\left(\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor+{c}_{{n}} \right)\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{4}^{{n}} \left({n}!\right)^{\mathrm{2}} } \\ $$$${Stirling}: \\ $$$${x}!\:\sim\:\sqrt{\mathrm{2}\pi{x}}\:\left(\frac{{x}}{{e}}\right)^{{x}} \\ $$$$\Rightarrow\left(\mathrm{2}{n}\right)!\:\sim\:\sqrt{\mathrm{4}\pi{n}}\left(\frac{\mathrm{2}{n}}{{e}}\right)^{\mathrm{2}{n}} =\sqrt{\mathrm{4}\pi{n}\:}\mathrm{4}^{{n}} \:\left(\frac{{n}}{{e}}\right)^{\mathrm{2}{n}} \\ $$$$\Rightarrow\left({n}!\right)^{\mathrm{2}} \:\sim\:\mathrm{2}\pi{n}\left(\frac{{n}}{{e}}\right)^{\mathrm{2}{n}} \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}} =\frac{\pi}{\mathrm{2}{n}}\left(\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor+{c}_{{n}} \right)\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{4}^{{n}} \left({n}!\right)^{\mathrm{2}} }\:\sim\:\frac{\pi}{\mathrm{2}{n}}\left(\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor+{c}_{{n}} \right)\frac{\sqrt{\mathrm{4}\pi{n}}}{\mathrm{2}\pi{n}} \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}} \sim\:\frac{\pi}{\mathrm{2}{n}}\left(\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor+{c}_{{n}} \right)\frac{\mathrm{1}}{\:\sqrt{\pi{n}}} \\ $$$${it}\:{is}\:{easy}\:{to}\:{see}\:{that}\:\frac{\pi}{\mathrm{2}{n}}\lfloor\frac{\mathrm{2}{n}}{\pi}\rfloor\sim\mathrm{1} \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}} \sim\:\frac{\mathrm{1}}{\:\sqrt{\pi{n}}} \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}} \rightarrow\mathrm{0} \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{we}\:{have}\:\mathrm{0}<{s}_{\mathrm{2}{n}+\mathrm{1}} <\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Rightarrow{s}_{\mathrm{2}{n}+\mathrm{1}} \rightarrow\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{s}_{{n}} \rightarrow\mathrm{0} \\ $$$$\Rightarrow\:{the}\:{only}\:{limiting}\:{point}\:{is}\:\mathrm{0}. \\ $$
Commented by hardmath last updated on 11/Aug/24

$$ \\ $$Dear professor, your solutions are perfect
