
Question Number 210421 by ajfour last updated on 08/Aug/24
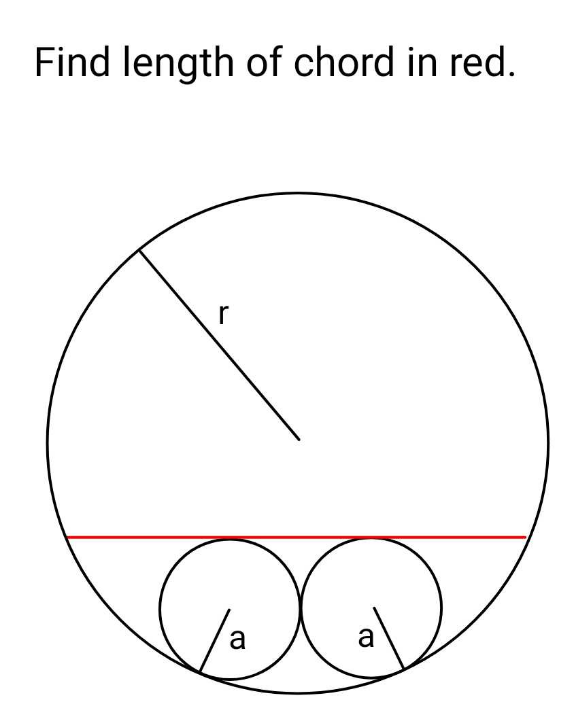
Answered by mr W last updated on 08/Aug/24
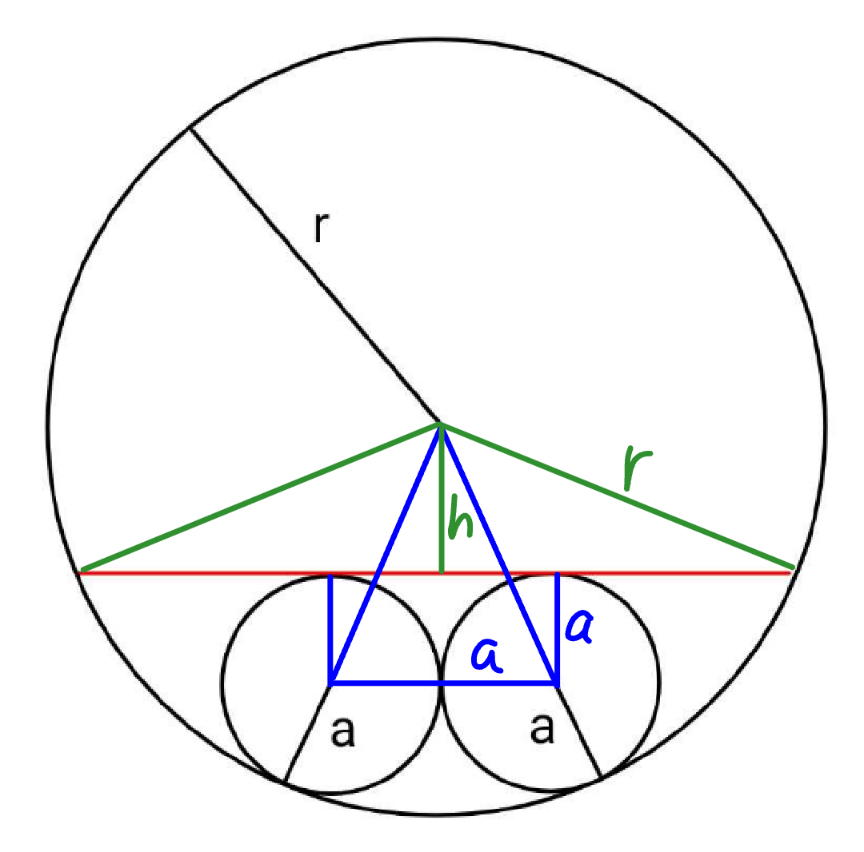
Commented by mr W last updated on 08/Aug/24
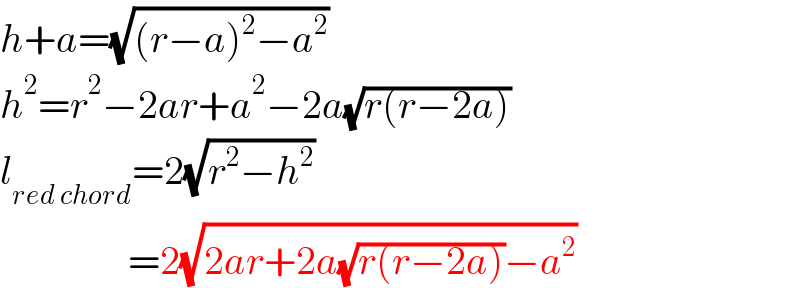
$${h}+{a}=\sqrt{\left({r}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$${h}^{\mathrm{2}} ={r}^{\mathrm{2}} −\mathrm{2}{ar}+{a}^{\mathrm{2}} −\mathrm{2}{a}\sqrt{{r}\left({r}−\mathrm{2}{a}\right)} \\ $$$${l}_{{red}\:{chord}} =\mathrm{2}\sqrt{{r}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{2}{ar}+\mathrm{2}{a}\sqrt{{r}\left({r}−\mathrm{2}{a}\right)}−{a}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 09/Aug/24
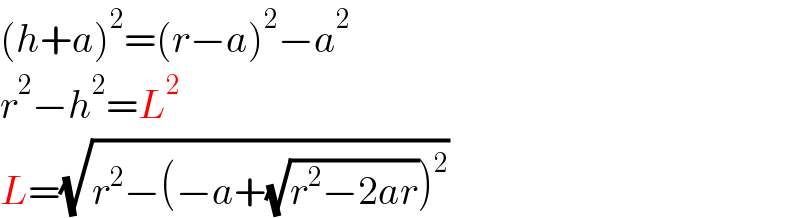
$$\left({h}+{a}\right)^{\mathrm{2}} =\left({r}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −{h}^{\mathrm{2}} ={L}^{\mathrm{2}} \\ $$$${L}=\sqrt{{r}^{\mathrm{2}} −\left(−{a}+\sqrt{{r}^{\mathrm{2}} −\mathrm{2}{ar}}\right)^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 09/Aug/24
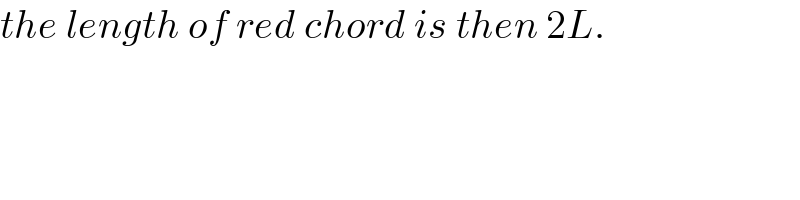
$${the}\:{length}\:{of}\:{red}\:{chord}\:{is}\:{then}\:\mathrm{2}{L}. \\ $$
Commented by ajfour last updated on 09/Aug/24
$${oh}\:{sure}.\:{thanks}\:{sir}. \\ $$
