Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 210396 by jirodomo last updated on 08/Aug/24

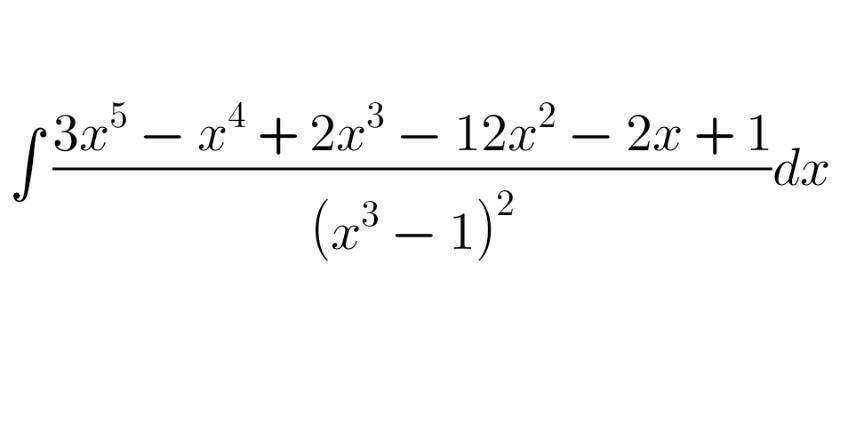
Commented by jirodomo last updated on 08/Aug/24

applying partial fraction decomposition straight away seems impossible here. is there other way? im stuck for a few months now.

$$\mathrm{applying}\:\mathrm{partial}\:\mathrm{fraction}\:\mathrm{decomposition} \\ $$$$\mathrm{straight}\:\mathrm{away}\:\mathrm{seems}\:\mathrm{impossible}\:\mathrm{here}. \\ $$$$\mathrm{is}\:\mathrm{there}\:\mathrm{other}\:\mathrm{way}?\:\mathrm{im}\:\mathrm{stuck}\:\mathrm{for}\:\mathrm{a}\:\mathrm{few} \\ $$$$\mathrm{months}\:\mathrm{now}. \\ $$

Commented by jhlombardi last updated on 08/Aug/24

divide de polinmio of the numbrer by the denominator polinimio

Answered by Frix last updated on 08/Aug/24

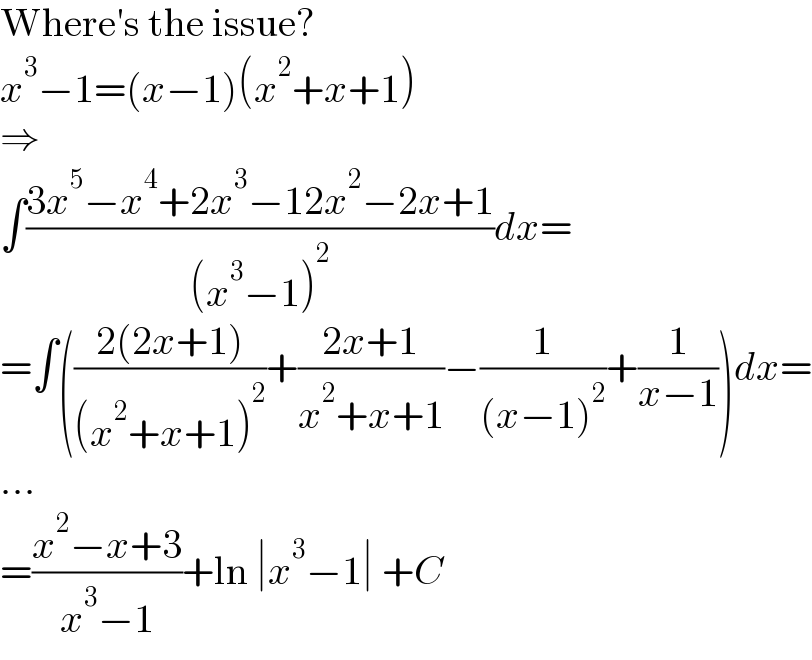
Where′s the issue? x^3 −1=(x−1)(x^2 +x+1) ⇒ ∫((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))dx= =∫(((2(2x+1))/((x^2 +x+1)^2 ))+((2x+1)/(x^2 +x+1))−(1/((x−1)^2 ))+(1/(x−1)))dx= ... =((x^2 −x+3)/(x^3 −1))+ln ∣x^3 −1∣ +C

$$\mathrm{Where}'\mathrm{s}\:\mathrm{the}\:\mathrm{issue}? \\ $$$${x}^{\mathrm{3}} −\mathrm{1}=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$$\int\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\int\left(\frac{\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}−\mathrm{1}}\right){dx}= \\ $$$$... \\ $$$$=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} −\mathrm{1}}+\mathrm{ln}\:\mid{x}^{\mathrm{3}} −\mathrm{1}\mid\:+{C} \\ $$

Commented by jirodomo last updated on 08/Aug/24

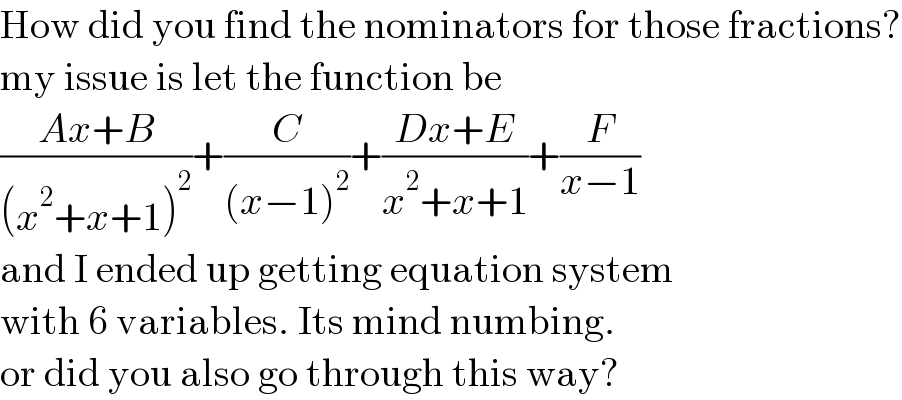
How did you find the nominators for those fractions? my issue is let the function be ((Ax+B)/((x^2 +x+1)^2 ))+(C/((x−1)^2 ))+((Dx+E)/(x^2 +x+1))+(F/(x−1)) and I ended up getting equation system with 6 variables. Its mind numbing. or did you also go through this way?

$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{nominators}\:\mathrm{for}\:\mathrm{those}\:\mathrm{fractions}? \\ $$$$\mathrm{my}\:\mathrm{issue}\:\mathrm{is}\:\mathrm{let}\:\mathrm{the}\:\mathrm{function}\:\mathrm{be} \\ $$$$\frac{{Ax}+{B}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{C}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{{Dx}+{E}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{{F}}{{x}−\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{ended}\:\mathrm{up}\:\mathrm{getting}\:\mathrm{equation}\:\mathrm{system} \\ $$$$\mathrm{with}\:\mathrm{6}\:\mathrm{variables}.\:\mathrm{Its}\:\mathrm{mind}\:\mathrm{numbing}. \\ $$$$\mathrm{or}\:\mathrm{did}\:\mathrm{you}\:\mathrm{also}\:\mathrm{go}\:\mathrm{through}\:\mathrm{this}\:\mathrm{way}? \\ $$

Commented by Frix last updated on 08/Aug/24

Search the www for Ostrogradski′s Method to see the proof. ∫((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))dx= =((Ax^2 +Bx+C)/(x^3 −1))+∫((Dx^2 +Ex+F)/(x^3 −1))dx Now differentiate both sides: ((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))= =−((Ax^4 +2Bx^3 +3Cx^2 +2Ax+B)/((x^3 −1)^2 ))+ +((Dx^2 +Ex+F)/(x^3 −1)) Multiplicate with (x^3 −1)^2 and transform (D−3)x^5 −(A−E−1)x^4 −(2B−F+2)x^3 −(3C+D−12)x^2 −(2A+E−2)x −(B+F+1) =0 ⇒A=1, B=−1, C=D=3, E=F=0 Now we have ∫((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))dx= =((x^2 −x+3)/(x^3 −1))+3∫(x^2 /(x^3 −1))dx

$$\mathrm{Search}\:\mathrm{the}\:\mathrm{www}\:\mathrm{for}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method} \\ $$$$\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{proof}. \\ $$$$\int\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{Ax}^{\mathrm{2}} +{Bx}+{C}}{{x}^{\mathrm{3}} −\mathrm{1}}+\int\frac{{Dx}^{\mathrm{2}} +{Ex}+{F}}{{x}^{\mathrm{3}} −\mathrm{1}}{dx} \\ $$$$\mathrm{Now}\:\mathrm{differentiate}\:\mathrm{both}\:\mathrm{sides}: \\ $$$$\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=−\frac{{Ax}^{\mathrm{4}} +\mathrm{2}{Bx}^{\mathrm{3}} +\mathrm{3}{Cx}^{\mathrm{2}} +\mathrm{2}{Ax}+{B}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }+ \\ $$$$+\frac{{Dx}^{\mathrm{2}} +{Ex}+{F}}{{x}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\mathrm{Multiplicate}\:\mathrm{with}\:\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{and}\:\mathrm{transform} \\ $$$$\left({D}−\mathrm{3}\right){x}^{\mathrm{5}} \\ $$$$−\left({A}−{E}−\mathrm{1}\right){x}^{\mathrm{4}} \\ $$$$−\left(\mathrm{2}{B}−{F}+\mathrm{2}\right){x}^{\mathrm{3}} \\ $$$$−\left(\mathrm{3}{C}+{D}−\mathrm{12}\right){x}^{\mathrm{2}} \\ $$$$−\left(\mathrm{2}{A}+{E}−\mathrm{2}\right){x} \\ $$$$−\left({B}+{F}+\mathrm{1}\right) \\ $$$$=\mathrm{0} \\ $$$$\Rightarrow{A}=\mathrm{1},\:{B}=−\mathrm{1},\:{C}={D}=\mathrm{3},\:{E}={F}=\mathrm{0} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} −\mathrm{1}}+\mathrm{3}\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{1}}{dx} \\ $$

Commented by jirodomo last updated on 09/Aug/24

thanks a lot. this is the first time i see this method. ill get it to very good use next time

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{first}\:\mathrm{time}\:\mathrm{i}\:\mathrm{see} \\ $$$$\mathrm{this}\:\mathrm{method}.\:\mathrm{ill}\:\mathrm{get}\:\mathrm{it}\:\mathrm{to}\:\mathrm{very}\:\mathrm{good}\:\mathrm{use} \\ $$$$\mathrm{next}\:\mathrm{time} \\ $$

Commented by Frix last updated on 09/Aug/24

It′s important to know when it′s possible to use and when not.

$$\mathrm{It}'\mathrm{s}\:\mathrm{important}\:\mathrm{to}\:\mathrm{know}\:\mathrm{when}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible} \\ $$$$\mathrm{to}\:\mathrm{use}\:\mathrm{and}\:\mathrm{when}\:\mathrm{not}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com